Решение. Пример расчета (задача № 10)

Пример расчета (задача № 10)

Для схем стальных балок I и II, изображенных на рис. 5.25 и 5.26, определить методом начальных параметров углы поворота се­чения и прогиб в точке D. Модуль упругости Е = 2×10⁸ кН/м². По­перечные сечения балок: схема I - круглое диаметром d = 0,24 м, схема II - квадратное со стороной a = 0,2 м.

Схема I.

1. Определение опорных реакций балки (рис. 5.25)

S y = 0, R ₀ + q × c - P = 0, R ₀ = - q × c + P = -10×1,4 + 12 = -2 кН;

S M ₀ =0, ,

M ₀ = q c (b + 0,5 c) - M - P (b + c + e) = 10×1,4×(1,8 + 0,5×1,4) -

- 20 - 12×(1,8 + 1,4 + 1,2) = -37,8 кН×м.

Рис. 5.25

Для проверки правильности определения опорных реакций сос­тавим уравнения равновесия:

å M_D = 0, M ₀ + R ₀×4,4 + q × c ×(0,5× c + e) + M = -37,8 - 2×4,4 +

+ 10×1,44×(0,5 1,4 + 1,2) + 20 = 46,6 - 46,6 = 0.

Реакции найдены верно.

2. Применение метода начальных параметров. Исполь­зуя уравнение (5.23), для нашего случая запишем:

E I_x y (z) = E I_x y ₀ + 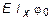z + -

- + .

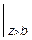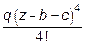
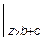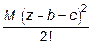
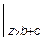Здесь M ₀ и Q ₀ - момент и реакция в заделке (т.е. в начале коор­динат). Знак ½ _{z > a} означает, что слагаемое, после которого он сто­ит, нужно учитывать при z > a и не надо - при z £ a. Начальные параметры имеют значения: y ₀ = 0; j₀ = 0; M ₀ = -37,8 кН×м, R ₀ =
= -2 кН (знак реакций определяется по знаку перемещения выз­ванного этими усилиями). Тогда выражение для определения про­гибов будет иметь вид:

E I y (z) = - - +
+ .

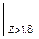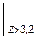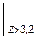Соответственно выражение для определения углов поворота бу­дет:

=-37,8× z - z ² + - +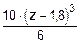
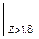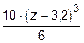
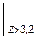+ 20×(z - 3,2) .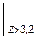

С помощью этих выражений определяем y_D и j _D:

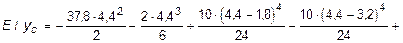
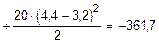кН×м³.

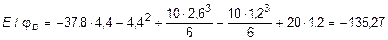кН×м².

Жесткость сечения при Е = 2×10⁸ кН/м² равна:

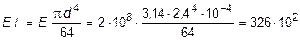кН×м².

Тогда, окончательно:

Прогиб точки D происходит вниз, а сечение поворачивается по часовой стрелке.

Схема II.

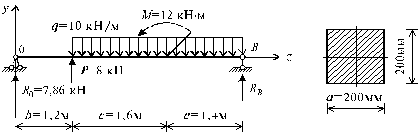
Рис. 5.26

1. Определение опорных реакций балки (рис. 5.26).

S M ₀ =0, R_B (b + c + e) - q ×(c + e)×[ b + 0,5×(c + e)] + M + P b = 0,

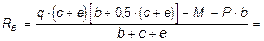
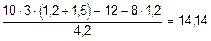= кН;

S M_B =0, R ₀ (b + c + e) - 0,5× q ×(c + e)² - M + P ×(c + e) = 0,

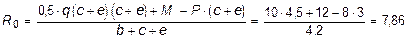кН.

Для проверки правильности определения опорных реакций сос­тавим уравнение равновесия сил по оси y:

S y =0; R ₀ + R_B + P - q (c + e) = 7,86 + 14,14 + 8 - 10×3 = 30 - 30 = 0.

Реакции найдены верно.

2. Применение метода начальных параметров. Исполь­зуя метод начальных параметров, для рассматриваемой балки запи­шем:

Из условий закрепления балки при z = 0 имеем: y ₀ = 0; М ₀=0.

Подставляя числовые значения, получим:

.

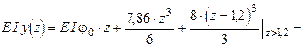
В данном выражении неизвестно j₀. Из условия закрепления балки при z = b + c + e имеем, что y = 0. Вычисляя прогиб на правом конце балки и приравнивая его к нулю, получим уравнение для определения j₀:

.

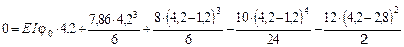Отсюда E I j₀ = -20,84 кН×м². Теперь выражение для определе­ния прогибов будет иметь вид:

.

Соответственно, выражение для определения углов поворота будет:

.

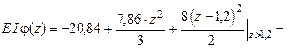
С помощью этих выражений определяем y_D и j _D:

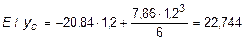кH×м³.

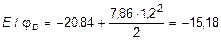кН×м².

Вычисляем жесткость сечения (Е = 2×10⁸ кН/м²):

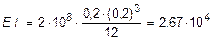кН×м².

Тогда, окончательно,

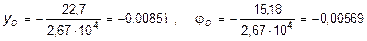рад.

Перемещение точки D происходит вниз, а сечение поворачива­ется по часовой стрелке.

Дата добавления: 2015-06-30