Решение. Пример расчета (задача № 13)

Пример расчета (задача № 13)

Дан пространственный консольный брус с ломаным очертани­ем осевой линии, нагруженный сосредоточенной силой Р = 1 кН и равномерно распределенной нагрузкой q = 2 кН/м. На рис. 5.34, а этот брус показан в аксонометрии в соответствии с прямоугольной системой координат xyz. Вертикальный элемент бруса имеет попе­речное сечение в виде круга диаметром d = 0,06 м (рис. 5.34, в), горизонтальные элементы бруса имеют поперечные сечения в виде прямоугольника (рис. 5.34, б). Ширина сечения b = d = 0,06 м, а высота сечения c = 0,5 d = 0,03 м. Ориентация главных осей попе­речных сечений на каждом участке показана на рис. 5.34, г.

Требуется:

1. Построить в аксонометрии эпюры M_x, M_y, M_z, N_z, Q_x, Q_y;

2. Указать вид сопротивления для каждого участка бруса;

3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N_z, M_x, M_y и M_z (касатель­ными напряжениями от Q_x и Q_y можно пренебречь);

4. Проверить прочность при расчетном сопротивлении R = = 180 МПа.

1. Построить в аксонометрии эпюры M_x, M_y, M_z, N_z, Q_x, Q_y. Заметим, что так как заданная система пространственная, при произвольном характере нагружения, в опорном сечении, где установлена заделка, возникает шесть опорных реакций (три опор­ные силы и три момента). Для определения опорных реакций, в данном случае, можем применить шесть уравнений равновесия ста­тики. Так как число независимых уравнений равновесия равно чис­лу опорных реакций, то можно сделать вывод, что рассматриваемая система в виде ломаного бруса, с заделанным одним концом, явля­ется статически определимой. Поэтому рассматриваемая система разрешима по методу сечений. Далее, учитывая особенности конст­рукции, определение величин внутренних усилий можно осущест­вить без предварительного вычисления величин опорных реакций.

Брус имеет три участка АВ, ВС и СD (рис. 5.34, г). При этом, после рассечения бруса на две части будем рассматривать равно­весие оставшейся части, не связанной с заделкой (чтобы избежать предварительного определения опорных реакций в заделке бруса). Внутренние силовые факторы можно рассматривать как реакции, действующие в сечении на оставшуюся часть со стороны отбро­шенной части, поэтому процесс определения шести величин M_x, M_y, M_z, N_z, Q_x, Q_y может быть сведен к известному процессу оп­ределения опорных реакций.

Следует отметить, что при определении опорных реакций их направление можно указать произвольно, а затем из решения урав­нения равновесия будет ясно, как в действительности действует ре­акция: если результат положительный, то реакция действует имен­но так, как мы предварительно указали, если отрицательный - то наоборот.

При построении эпюр будем руководствоваться следующими правилами:

- нормальная сила N_z считается положительной, если она вызы­вает растяжение бруса;

- крутящий момент M_z считается положительным, если при взгляде на сечение со стороны внешней нормали он виден враща­ющим брус по ходу часовой стрелки;

- поперечная сила Q_x считается положительной, если при взгляде со стороны положительного направления оси y она стре­мится вращать оставшуюся часть бруса по ходу часовой стрелки от­носительно ближайшей точки на оси бруса (для поперечной силы Q_y - то же, по отношению к x);

- ординаты эпюр Q_x и Q_y следует откладывать перпендикуляр­но оси бруса в плоскости действия этих сил и указывать знак;

- ординаты эпюр М_x и М_y будем откладывать перпендикулярно оси бруса со стороны растянутого волокна.

Участок АВ (0 £ z ₁ £ a ).

Оставшаяся часть изображена на рис. 5.34, д. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 5.34, г. Коор­дината z ₁ увеличивается от точки А к точке В. Для определения N покажем ее в направлении от сечения, т.е. растягивающей, и соста­вим уравнения равновесия: S z = 0; N_z = 0. Из å М_x = 0 следует М_x = 0 (рис. 5.35, а).

Для определения М_z покажем его так, чтобы при взгляде на сечение он был виден вращающим брус по часовой стрелке, и составим уравнения равновесия (рис. 5.35,б):

S m_z = 0; М_z = 0.

Для определения Q_x и Q_y покажем их положительными в соот­ветствии с выбранным правилом знаков и составим уравнения рав­новесия:

S x = 0, Q_x - P = 0, Q_x = P = 1 кН;

S y = 0, Q_y = 0.

Эпюра Q_x представляет собой прямоугольник (рис. 5.35, в) с ординатой, равной 1, лежащей в плоскости действия этого силово­го фактора. Составляем уравнение равновесия:

S M_y = 0, М_y + Р × z = 0, М_y = - P × z.

Ординаты эпюры M_y линейно зависят от z:

z = 0, M_y = 0; z = a, M_y = - P × a = -1×0,3 = -0,3 кН×м.

Знак минус указывает на то, что в действительности изгибаю­щий момент M_y вызывает растягивающее напряжение в правой части поперечного сечения, поэтому ординаты эпюры M_y отклады­ваются в правую сторону.

Участок ВC (0 £ z ₂ £ b ).

Оставшаяся часть изображена на рис. 5.34, e. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 5.34, г. Коор­дината z ₂ увеличивается от точки В к точке С. Процесс опреде­ления внутренних силовых факторов на этом участке такой же, как и на предыдущем. Важно отметить, что на оставшейся части соот­ветствующий внутренний силовой фактор удобно показывать непо­средственно перед его определением - для того, чтобы не затем­нить чертеж. При этом N_z, M_z, Q_x, Q_y показывают в положи­тельном направлении в соответствии с принятым правилом знаков, а изгибающие моменты M_x и M_y - наугад из двух возможных направлений (рис. 5.34, e):

S z = 0, N_z = 0; S M_z = 0, M_z + P × a = 0, M_z = - P × a = -0,3 кН×м.

Плоскость прямоугольной эпюры произвольна (рис. 5.35, б).

S x = 0, Q_x - P = 0, Q_x = P = 1 кН.

Эпюра Q_x в виде прямоугольника показана на рис. 5.35, в.

S y = 0, Q_y - q z = 0; Q_y = q z;

z = 0, Q_y = 0; z = 0,6 м, Q_y = 2×0,6 = 1,2 кН.

Эпюра Q_y в виде треугольника показана на рис. 5.35 е.

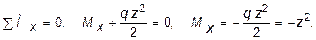
Рис. 5.35

Ординаты M_x изменяются по закону квадратной параболы.

z = 0, M_x = 0; z = 0,6 м, M_x = -0,36 кН×м;

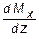= 2 z = 0; z = 0- точка экстремума в эпюре M_x в сечении z = 0.

Знак минус указывает, что растягивающие напряжения возни­кают не в ближней части сечения, а в дальней. При этом наблюда­тель ориентирован относительно глобальной системы координат xy, показанной на рис. 5.34, а следующим образом: ось x направле­на к наблюдателю, поэтому ординаты M_x откладываем в дальнюю сторону (рис. 5.35, а).

S M_y = 0, M_y + P z = 0, M_y = - P z;

z = 0, M_y = 0; z = 0,6 м, M_y = -0,6 кН×м.

Эпюра M_y - треугольная. Растягивающие напряжения возника­ют в правой части сечения - ординаты откладываем вправо.

Участок CD (0 £ z ₃ £ c ₁).

Оставшаяся часть изображена на рис. 5.34, ж. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 5.34, г. Коор­динаты z ₃ увеличиваются от точки С к точке D. Повторяя все рас­суждения, проведенные на предыдущих участках, будем иметь следующее (рис. 5.34, д):

S z = 0, N - P = 0, N = P = 1 кН;

S M_z = 0, 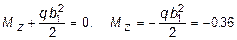кН×м.

Эпюра M_z - в виде прямоугольника. Плоскость изображения произвольная:

S x = 0, Q_x + q b ₁ = 0, Q_x = - q b ₁ = -2×0,6=-1,2 кН.

Эпюра Q_x - в виде прямоугольника в плоскости действия Q_x.

S y = 0, Q_y = 0;S M_x = 0, M_x + P b ₁ = 0, M_x = - P b ₁ = -0,6 кН×м.

Эпюра M_x - в виде прямоугольника. Растягивающие напряже­ния при изгибе возникают в нижней части поперечного сечения -ординаты эпюры откладываем вниз.

S M_y = 0, M_y + P a - q b ₁ z ₃ = 0, M_y = q b ₁ z ₃ - P a = 1,2 z ₃ - 0,3.

Величина M_y определяется как линейная функция от z ₃. При z ₃ = 0; M_y = -0,3 кН×м. В этом сечении растягивающие напряжения возникают не в дальней части сечений, а в ближней - ординату откладываем к наблюдателю.

При z ₃ = 0,5м M_y = 1,2×0,5 - 0,3 = 0,6-0,3 = 0,3 кН×м.

В этом сечении M_y откладываем от наблюдателя (рис. 5.35, г).

2. Установить вид сопротивления для каждого участка бруса. По эпюрам устанавливаем вид сопротивления на каждом участке бруса. На участке АВ возникают изгибающий момент M_y и поперечная сила Q_x, что свидетельствует о наличии поперечного изгиба. На участке ВС возникают изгибающие момен­ты M_x, M_y, поперечные силы Q_x, Q_y и крутящий момент M_x, что свидетельствует о наличии косого изгиба и кручения. На участке СD действуют изгибающие моменты M_x и M_y, поперечная сила Q_x, растягивающая сила N и крутящий момент M_z, что свиде­тельствует о наличии косого изгиба с растяжением и кручением.

3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N, M_x, M_y и M_z (касательными напряжениями от Q_x и Q_y можно пренебречь). Участок АВ. Наибольшая величина изгибающего момента M_y, судя по эпюре (рис. 5.35, г) возникает в сечении, бесконечно близком к точке В. Максимальные нормаль­ные напряжения при изгибе определяются по формуле:

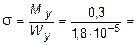16,7×10³ кН/м²,

где момент сопротивления W_y = 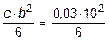=1,8×10^-5 м³.

Участок ВС. По эпюрам M_x и M_y устанавливаем, что опасным является сечение, бесконечно близкое к точке С. Для круглого сечения суммарный изгибающий момент:

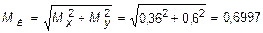кН×м,

а наибольшие нормальные напряжения равны:

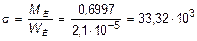кН/м²=33,32 МПа,

где момент сопротивления круглого сечения при изгибе:

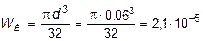м³ .

При кручении круглого сечения возникают касательные на­пряжения, максимальные значения которых определяются по фор­муле:

,

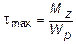где W_p - момент сопротивления при кручении. Известно, что

W_p = 2 W_И = 2×2,1×10⁵ м³ = 4,2×10⁵ м³,

тогда

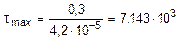кПа=7,143 МПа.

Участок СD. По эпюрам M_x и M_y видим, что равными по опасности будут сечения, бесконечно близкие к точкам С и D. При действии растягивающей силы N во всех точках поперечного сече­ния возникают одинаковые нормальные напряжения:

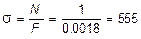кН/м² = 0,555 МПа,

где F = b × c = 0,06×0,03=0,0018 м² - площадь поперечного сечения;

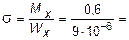66666 кН/м² = 66,67 МПа,

где

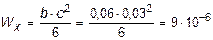м³.

При действии изгибающего момента M_y наибольшие нормаль­ные напряжения будут равны:

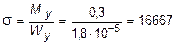кН/м² = 16,67 МПа.

При кручении бруса прямоугольного сечения возникают каса­тельные напряжения, максимальные значения которых определятся по формуле:

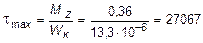кН/м² = 27,07 МПа,

где W_K = b× c ³ = 0,493×0,03³ = 13,3×10^-6 м³ - геометрическая величи­на, играющая роль момента сопротивления при кручении стержней прямоугольного сечения. Здесь b - коэффициент, зависящий от от­ношения большей стороны прямоугольника к меньшей (в данном случае при b / c = 2, b = 0,493).

4. Проверка прочности при расчетным сопротивле­нии R = 180 МПа. Расчетное напряжение по третьей теории прочности для плоского напряженного состояния определяется по формуле:

.

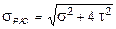Участок АВ. Линейное напряженное состояние является част­ным случаем плоского (t = 0), поэтому в нашем случае:

, где R = 180 МПа.

Участок ВС. Проверка прочности по третьей теории:

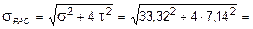36,25 МПа < 180 МПа.

Участок СD. Сначала найдем максимальное нормальное напря­жение от внутренних силовых факторов N, M_x и M_y:

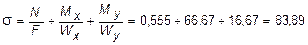МПа.

Касательные напряжения в угловой точке от кручения равны 0. Имеет место линейное напряженное состояние:

МПа < 180 МПа.

Далее рассмотрим напряженное состояние в окрестности точки, где действует максимальное касательное напряжение t = 27,7 МПа. Имеет место плоское напряженное состояние:

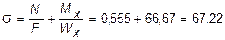МПа;

МП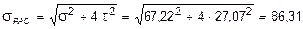а < 180 МПа.

Следовательно, так как условие обеспечения прочности во всех опасных точках участков ломанного бруса выполняются, то проч­ность конструкции в целом следует считать обеспеченной.

6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
СИСТЕМ МЕТОДОМ СИЛ

6.1. Стержневые системы.
Степень статической неопределимости

Под стержневой системой понимается всякая конструк­ция, состоящая из элементов, имеющих форму бруса. Если эле­менты конструкции работают только на растяжение или сжатие си­стема называется фермой (рис. 6.1). Ферма состоит из шарнирно опертых между собой прямых стержней, образующих треугольники и для нее характерно приложение внешних сил в узлах заданной системы.

Если элементы стержней системы работают в основном на изгиб или кручение, то такая система называется рамой (рис. 6.2).

Если все элементы стержневой системы расположены в одной плоскости, в которой также действуют все внешние силы, включая реакции опор, то система называется плоской (рис. 6.1, 6.2).

Если все элементы заданной системы расположены в одной плоскости, а внешние силы действуют в перпендикулярной плос­кости, то система называется плоскопространственной (рис. 6.3). Стержневые системы, не относящиеся к двум указанным категориям, называются пространственными (рис. 6.4).

Все стержневые системы принято разделять на статически определимые и статически неопределимые. Под статически определимой понимается такая система, для которой усилия во всех ее элементах могут быть определены по методу сечений с применением лишь урав­нений равновесия. Если этого сделать нельзя, то такая система на­зывается статически неопределимой.

Разность между числом неизвестных усилий (реакций опор и внутренних силовых факторов) и числом независимых уравнений равновесий, которые могут быть составлены для рассматриваемой сис­темы, называется степенью статической неопредели­мости системы.

Связи, наложенные на систему, бывают внешними и внутрен­ними. Под внешними понимают ограничения, накладываемые на абсолютные перемещения точек системы, как единое целое. Внутренние же связи ограничивают взаимные (относительные) перемещения элементов системы. Следовательно, статическая неопределимость системы мо­жет быть вызвана как внешними, так и внутренними связями.

Если рассматривать внешние связи, то можно отметить, что по­ложение жесткого тела на плоскости x,y характеризуется тремя незави­симыми параметрами - координатами x, y и углом поворота рассматриваемой плоскости. Таким образом, необходимое для равновесия число наложен­ных внешних связей должно быть равно трем (по количеству уравнений равновесия - å x = 0, å y = 0, å m = 0). Если плоская система состоит из D частей, каждую из которых можно рассмат­ривать как жесткое тело, то количество параметров, определяющих положение этой системы будет равно 3 D. Каждый шарнир, соеди­няющий две части системы, разрешает лишь их взаимный поворот, устраняя возможность их взаимных смещений - следовательно он уменьшает количество возможных перемещений системы на две единицы. Кроме этого, каждый опорный стержень устраняет воз­можность перемещения системы в соответствующем направлении. Таким образом, подсчитать степень статической неопределимости системы, определяемую внешними связями, можно по следующей формуле:

W = 3 D - 2 Ш - С,

где D - число частей (“дисков”) системы, каждая из которых может рассматриваться как абсолютно жесткое тело, Ш - количество шар­ниров в системе, соединяющих “диски”, С - число опорных стерж­ней. Для статически определимых систем W =0. При W<0 система является статически неопределимой.

Наиболее характерные типы внешних связей и их схематичные изображения рассмотрены в п. 5.1.

На рис. 6.5 показана плоская рама, имеющая в первом (а) случае три внешние связи, а во втором случае (б) - пять. Значит, в первом случае рама имеет необходимое для статической определи­мости количество внешних связей, а во втором же - две дополни­тельные внешние связи. Однако в обеих ситуациях рама статически неопределима, т.к. конфигурация ее такова, что не позволяет опре­делить усилия во всех ее элементах, используя только уравнения равновесия. Следовательно, для окончательного ответа на вопрос о статической определимости системы необходимо проведение сов­местного анализа наложенных на систему внешних и внутренних связей (более подробно этот вопрос рассматривается в курсе строи­тельной механики).

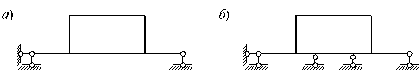
Рис. 6.5

Методы расчета статически неопределимых систем основаны на определении перемещений в ее точках. Выше мы рассматривали метод начальных параметров для вычисления перемещений в бал­ках. При всех достоинствах этого метода он обладает одним суще­ственным недостатком - при большом количестве участков вычис­лительные формулы становятся весьма громоздкими. Особенно это существенно в случае криволинейной оси стержневой системы.

В связи с этим, рассмотрим более универсальный метод опре­деления перемещений - метод Мора, названный так по имени немецкого ученого, предложившего его.

Дата добавления: 2015-06-30