Определение перемещений методом Мора. Суть метод Мора в следующем

Суть метод Мора в следующем. Если необходимо определить перемещение в заданной точке по заданному направлению, то на­ряду с заданной системой внешних сил в этой точке прикладыва­ется внешнее усилие Ф = 1 в интересующим нас направлении.

Далее составляется выражение потенциальной энергии систе­мы, состоящей из n участков с учетом одновременного действия заданной системы внешних сил и силы Ф:

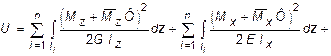
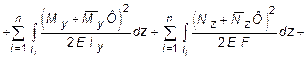(6.1)

,

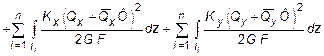где К_х , К_у - безразмерные величины, зависящие от геометрической формы сечения и учитывают неравномерность распределения каса­тельных напряжений в сечении при поперечном изгибе. Так, на­пример, для прямоугольника К_х = К_у = 1,2, а для двутавра при из­гибе в плоскости его стенки K = F / F_CT, где F - площадь всего сечения двутавра, F_CT - площадь стенки; N_z, Q_x, Q_y, M_z, M_x, M_y - внутренние силовые факторы, возникающие в поперечных сечениях заданной стержневой системы; 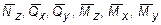-внутренние силовые факторы, возникающие в поперечных сечени­ях заданной системы, от действия усилия Ф = 1.

Дифференцируя выражение (6.1) по Ф, и полагая после этого Ф = 0, находим искомое перемещение в искомой точке в нужном направлении.

. (6.2)

Полученные интегралы называются интегралами Мора и ши­роко применяются при вычислении перемещений стержневых сис­тем.

Для систем, элементы которых работают на растяжение или сжатие (например, шарнирно-стержневые системы - фермы), в формуле Мора (6.2) отличен от нуля будет только слагаемое, содер­жащее продольные силы. При расчете балок или рамных систем, работающих в основном на изгиб, влияние поперечной и продоль­ной силы на перемещение несущественно и в большинстве случаев их влияние не учитывается. В случае пространственной работы стержня или стержневой системы, элементы которой работают, в основном, на изгиб и кручение, в формуле Мора обычно ограничи­ваются рассмотрением слагаемых, содержащих изгибающие и кру­тящие моменты.

Подробно рассмотрим случай, когда брус работает только на изгиб (M_x ¹ 0, N_z = M_z = M_y = Q_x = Q_y = 0). В этой ситуации вы­ражение (6.2) принимает вид:

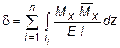. (6.3)

Согласно (6.3) для определения перемещения произвольной точки в произвольном направлении, последовательно необходимо выполнять следующее:

1. Построить эпюру моментов М_x от заданной системы внеш­них сил;

2. Исключая внешние силы и в точке, где необходимо опре­делить перемещение по заданному направлению, прикладывается единичное усилие (сила - если требуется определить линейное пе­ремещение; момент - если требуется определить угловое перемеще­ние), и от действия единичного усилия строится эпюра моментов ;

3. По формуле Мора (6.3) вычисляется искомое перемещение.

Рис. 6.6

Если принять E I = const, то перемещение в некоторой точке стержня определяется как интеграл от произведения двух функций моментов - М_x и . В общем виде инте­грал Мора можно выразить следующей формулой:

. (6.4)

Часто встречаются случаи, когда на участке стержня дли­ной l необходимо вычислить интеграл Мора при условии, что по крайней мере одна из функций - линейная (рис. 6.6). Пусть f ₂ = b + k z, тогда из (6.4) получим:

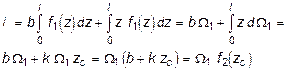(6.5)

где W₁ - площадь эпюры f ₁; f ₂ (z_C) - ордината линейной эпюры под центром тяжести криволинейной эпюры (рис. 6.6).

Приведенное решение носит имя русского ученого Верещагина, впервые его получившего. Таким образом, по способу Вереща­гина операция интегрирования выражения (6.4) в случае линей­ности хотя бы одной из подынтегральных функций существенно упрощается и сводится к перемножению площади криволинейной эпюры на ординату второй (линейной) функции под центром тя­жести криволинейной.

Используя способ Верещагина, приведем результаты вычисле­ния интегралов Мора для двух наиболее часто встречающихся слу­чаев:

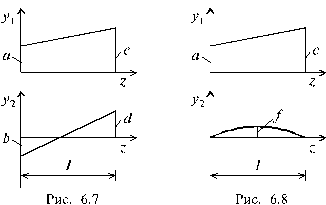
1. Обе функции f ₁ и f ₂ - линейные (рис. 6.7), тогда

; (6.6)

2. Функция f ₁ - квадратная парабола, f ₂ - линейная функция (рис. 6.8). Такая ситуация встречается, когда на участке длиной l приложена равномерно распределенная нагрузка q, тогда

, (6.7)

где f - “стрелка” квадратной параболы (рис. 6.8), .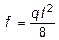

В общем случае, если площадь W эпюры моментов имеет слож­ную геометрию и представляется возможным ее разбить на пло­щади W _k (k = 1,2,3,...), имеющие элементарную геометрию, то ин­теграл Мора I от произведения эпюры W на эпюру моментов M, может быть представлен в виде:

. (6.8)

Для расчета усилий в статически неопределимых стержневых системах существуют различные методы. Здесь рассмотрим метод сил.

Дата добавления: 2015-06-30