Условие статической прочности вала при кручении имеет вид

Пример расчета (задача № 17)

Пример расчета (задача № 16)

Определить динамический прогиб и напряжения в опасных се­чениях балок КD и АВ, возникающих под действием работающего электромотора весом G = 10 кН (рис. 8.4, а). Вес неуравновешан­ных частей ротора Р = 1 кН. Эксцентриситет вращающихся масс е = 0,02 м. Число оборотов ротора n = 600 об/мин. Массой балок в расчетах пренебречь. Поперечное сечение балок КD и АВ состоит из двух двутавров №20 (I_x = 1840×10^-8 м⁴; W_x = 184×10^{-6 м3}). Модуль упругости стали Е = 2×10⁸ кН/м².

Рис. 8.4

Решение

1. Определение статического прогиба в сечении С балки КD и статического напряжения в сечении у задел­ки А. Из уравнений равновесия статики S m_D = 0 и S m_K = 0 найдем опорные реакции в балке КD (рис. 8.4, б):

кН.

На балку АВ в точке В (К) опоры на консоль передается нагруз­ка Р = 5 кН, равная по величине опорной реакции R_K , но обратная по направлению. Из уравнений S m_A = 0 и å y = 0 определяем реак­тивные усилия в заделке А балки АВ: М_A = 10 кН×м; R_А = 5 кН. Оп­ределив опорные реакции в балках, строим эпюры поперечных сил Q и изгибающих моментов М для балок КD и АВ (рис. 8.4, в, г, е, ж). Зная величины изгибающих моментов, возникающих в опас­ных сечениях балок, определяем статические напряжения в сечени­ях С и А:

кН/м²;

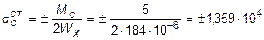кН/м².

Для определения статического прогиба в точке С балки КD вна­чале предполагаем, что эта балка опирается на абсолютно жесткое основание. Используя метод начальных параметров, составляем уравнение прогибов, приняв начало координат в сечении D.

,

где y ₀ = 0, М ₀ = 0, j₀ ¹ 0, .

Для нахождения j₀ составим уравнение прогиба для сечения К в котором прогиб равен нулю из условий закрепления:

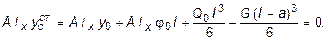
Так как y ₀ = 0, то, решая это уравнение, получим:

.

Подставив найденное значение j₀ в уравнение прогиба для се­чения С, получим формулу для определения :

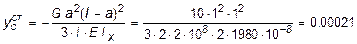м.

Для вычисления полного перемещения сечения С с учетом характера опирания балки КD на консольную балку необходимо найти прогиб консольной балки АВ от действия на нее силы Р_K = - R_K = 5 кН. Для этого, приняв начало координат в сечении В балки АВ, соста­вим уравнение метода начальных параметров для определения прогиба на конце консоли. При начале координат в точке В консоли известными параметрами будут: М ₀ = М_B = 0; Q ₀ = Q_B = - Р_K = -5 кН, а неизве­стными y ₀ = y_B ¹ 0; j₀ = j _B ¹ 0. Неизвестные начальные параметры y ₀ и j₀ определим из уравнений прогиба и угла поворота для сечения А. Из условия закрепления балки АВ имеем при z = l = 2 м y_A = j _А = 0.

Составим уравнения метода начальных параметров:

(а)

. (б)

Приравняв к нулю уравнение (а) при z = l м, определяем j₀:

.

Подставив найденное значение j₀ в уравнение (б) и принимая y = 0 при z = l, получим выражение второго неизвестного на­чального параметра y ₀, определяющего прогиб сечения В консоль­ной балки АВ:

;

;

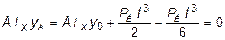м.

Знак “минус” говорит о том, что конец консольной балки пере­местится вниз.

Определив прогиб и изобразив эпюру перемещений систе­мы (рис. 8.4, з), вычислим величину полного перемещения сече­ния С по формуле:

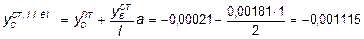м.

2. Определение динамического коэффициента и коэффициента эквивалентности. Макси­мальное значение системы внешних сил принимает значение G + b× P ₀. Далее определяем коэффициент эквивалентности:

,

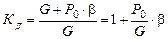где 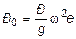- амплитудное значение инерционной силы; b = - коэффициент динамичности. Здесь -частота собственных колебаний; - частота возмущающей силы.

В рассматриваемом примере:

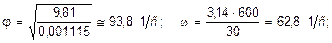
кН;

.

3. Определение прогиба и напряжений. Максимальное значение напряжения и прогиб, возникающие от совместного действия статических и дина­мических нагрузок, определяем по формулам:

кН/м²,

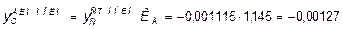м.

При коэффициенте К_Д = 1,145 найдем также напряжение в се­чении А балки АВ:

кН/м².

Следовательно, полученное значение напряжения больше, чем напряжение в сечении С, где установлен электромотор. Итак, сече­ние в заделке в данном примере является наиболее опасным , и, следовательно, это обстоятельство необходимо учитывать при проверке прочности составных конструкций.

С увеличением числа оборотов двигателя возрастают динамиче­ские напряжения и прогибы балок. Поэтому при проектировании конструкций не следует допускать наступления резонанса (w = j), при котором может наступить разрушение конструкции.

8.4. Соударение твердого тела и системы
с одной степенью свободы

Задача соударения различных механических систем часто встре­чается в инженерной деятельности в различных сферах, поэтому имеет большое практическое значение.

Взаимодействие тел, при котором за очень малый промежуток времени скачкообразно изменяются скорости взаимодействующих тел, называется ударом. В период взаимодействия соударяемых тел между ними развивается результирующая контактная сила. Хотя время действия контактной силы обычно очень мало и измеряется микро- или миллисекундами, она развивается очень быстро и принимает большие значения.

Задача соударения твердых деформируемых тел в механике, как правило, относится к классу динамических контактных задач со смешанными граничными условиями, содер­жащими в себе многие трудности математического порядка при их решении, которые не всегда могут быть преодолены простыми инженерными способами. Эти трудности в первую очередь связаны с определением с определением характера изменения функции напряжения в зоне контакта соударяемых тел по пространственным координатам и во времени. Большие сложности возникают и при учете волновых процессов, возникающих, как в зоне контакта, так и внутри соударяемых тел. Например, дифракционных волно­вых процессов по контуру в зоне контакта, и интерферен­ционных явлений внутри соударяемых тел. Здесь существенное значение приобретает и учет фактора рассеяния энергии, трудно поддающийся анализу в данном случае.

Исходя из вышеизложенного, ниже при решении задач, приме­няется упрощенный инженерный подход, основанный на следую­щих упрощающих предпосылках.

При взаимодействии соударяемых тел они принимаются или идеально упругими, или абсолютно твердыми. Деформации в упругих соударяемых телах происходят мгновенно.

С применением энергетического подхода рассмотрим соударе­ние падающего груза массой М с высоты h на систему с одной сте­пенью свободы (рис. 8.5). Считаем, что масса балки m сосредо­точена в месте соударения.

Рис. 8.5

Энергетический подход является наиболее предпочтительным в тех случаях, когда требуется определить только максимальные зна­чения напряжений, динамических прогибов и не ставится задача определения законов движения заданной системы.

Составим энергетический баланс заданной системы в момент возникновения максимальных прогибов балки:

К ₀ + П = U + К, (8.8)

где 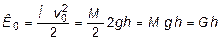- кинетическая энергия пада­ющего груза в момент соударения с балкой; П = (М + m)× g × y _max -работа внешних сил на перемещение y _max; 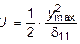- потен­циальная энергия деформации балки; К - кинетическая энергия системы при y = y _max.

Так как в состоянии наибольшего отклонения балки, y = y _max, 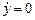, то для указанного момента времени К = 0. С учетом вышеизложенного (8.8) принимает вид:

, (8.9)

или

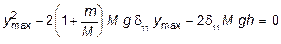. (8.10)

Величина d₁₁ - прогиб, который получила бы балка под дейст­вием единичной статической силы, приложенной в месте удара. Следовательно, y^CТ = M g d₁₁ представляет собой прогиб который получила бы балка под действием статически прикладываемой си­лы, равной весу падающего груза G = M g. Тогда уравнение (8.10) можно представить в виде:

.

Из решения последнего уравнения получаем:

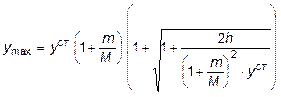. (8.11)

Отсюда, учитывая, что коэффициент динамичности определяет во сколько раз максимальный прогиб при динамическом нагру­жении больше прогиба, возникающего при статическом характере приложения нагрузки, получим:

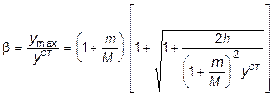. (8.12)

Величина коэффициента динамичности b, как показывает вы­ражение (8.12), зависит главным образом от жесткости рассмат­риваемой системы в направлении удара и от кинетической энергии падающего груза в момент соударения.

Для упругих систем динамические напряжения и остальные внутренние силовые факторы определяются по той же схеме, как и прогибы. Например, для напряжений, имеем:

s ^ДИН = b × s ^CТ. (8.13)

В тех случаях, когда масса балки m мала, по сравнению с мас­сой груза M, из (8.12), принимая m = 0, получим:

. (8.14)

В частности, если груз прикладывается на упругую систему мгновенно, тогда задавая h = 0 из (8.14), коэффициент динамичности принимает значение b = 2.

Груз G = 1,2 кН падает с высоты h = 0,12 м в точку С двутав­ровой балки КD, опирающейся на упругое сооружение, состоящее из двух балок АК и DМ (рис. 8.6, а). Сечение балки КD -двутавр №18 (I_x = 1290×10^-8 м⁴ ; W_x = 143×10^-6 м³). Сечение балок АК и DМ - двутавр №30 (I_x = 7080×10^-8 м⁴; W_x = 472×10^-6 м³). Длина ба­лок l = 1,2 м. Модуль упругости Е = 2×10⁸ кН/м².

Определить динамические напряжения в опасных сечениях ба­лок. Сравнить полученные напряжения с теми, которые появятся в балках, если балка КD будет опираться на абсолютно жесткое осно­вание.

Решение

Из уравнений равновесия балки S m_K = 0 и S m_D = 0 находим опорные реакции R_K , R_D :

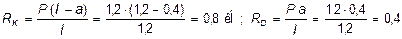кН.

Для проверки правильности найденных опорных реакций сос­тавляем уравнение равновесия S y = 0: 0,8 + 0,4 - 1,2 = 0; 0 = 0.

Затем строим эпюры изгибающих моментов и поперечных сил для рассматриваемой балки КD и двух консольных балок АК и DМ (рис. 8.6, б, в, г, д, е).

1. Определение полного статического прогиба сече­ния С балки КD. С начала определим статический прогиб сече­ния С балки КD при опирании ее на абсолютно жесткое основание. Составим уравнение прогиба методом начальных параметров, при­няв начало координат в сечении К:

. (8.15)

При этом, y ₀ = 0; M ₀ = 0; j₀ ¹ 0; Q ₀ = R_K . Для нахождения j₀ используем условие отсутствия прогиба в сечении D y_D = 0. При
z = l м имеем:

; .

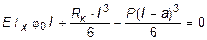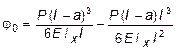Теперь, подставив найденное значение j₀ в уравнение (8.15), получим формулу для определения прогиба сечения С:

м.

Для определения полного прогиба сечения С с учетом упругого характера опирания балки КD (рис. 8.6, ж) необходимо предварительно найти прогибы концов консольных балок АК и DМ. Для этого воспользуемся фор­мулой, полученной в задаче № 16:

м;

м.

Эпюра перемещений для составной конструкции из балок изо­бражена на рис. 8.6, ж. Величину полного перемещения сечения С балки с учетом перемещения его в результате смещения опор балки КD, опирающейся на консольные балки, определяем по формуле:

.

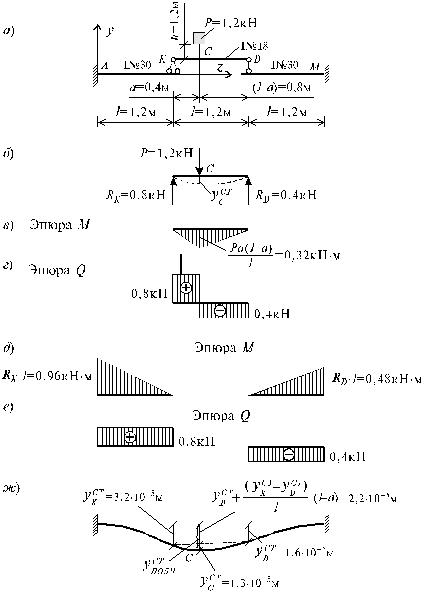
Рис. 8.6

2. Определение динамических коэффициентов и на­пряжений. Динамический коэффициент при падении груза G на балку КD, опирающуюся на консольные балки АК и DМ, опреде­ляем по формуле:

а при опирании балки КD на абсолютно жесткое основание -

.

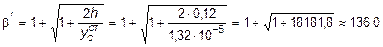Для вычисления динамических напряжений необходимо внача­ле определить статические напряжения, возникающие в сечении С:

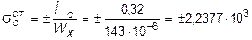кН/м²,

а затем динамические напряжения:

.

Динамические напряжения, возникающие в сечении С балки КD, опирающейся на консольные балки,

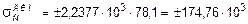кН/м²,

и динамические напряжения, возникающие в сечении С балки КD, опирающейся на абсолютно жесткое основание:

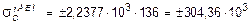кН/м².

Таким образом, если опоры лежат на абсолютно жестком осно­вание, то в сечении С возникают динамические напряжения в 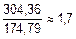раза большие по величине. Статические напряжения, возникающие в сечении А:

кН/м².

При динамическом коэффициенте К_Д = 78,1, полученном в предположении упругого опирания балки КD в точках К и D, нахо­дим динамические напряжения в сечении А:

кН/м².

Статическое и динамическое напряжения в сечении М балки DМ:

кН/м².

кН/м².

Следовательно, вне зависимости от того, на какое основание опирается балка KD, опасное сечение находится в точке удара.

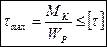
Задачи на условия прочности при кручении:

1. Проверка прочности

2. Проектный расчет круглого сплошного сечения ; ; .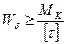

Кольцевого сечения ;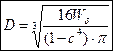

3. Определение максимально допустимой нагрузки

Дата добавления: 2015-06-30