Условия жесткости при кручении 3 страница

μ=2 μ=1 μ=0,7 μ=0,5

Коэффициент запаса устойчивости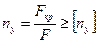

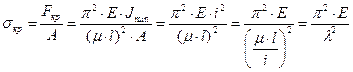; где 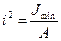, откуда 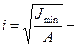радиус инерции сечения.

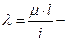гибкость стержня (величина безразмерная.

Формула Эйлера справедлива в пределах закона Гука.

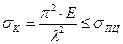здесь σ_ПЦ- предел пропорциональности материала стержня.

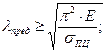
Предел применения формулы Эйлера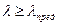

Формула Тетмайера – Ясинского (для стальных, дюралюминиевых и деревянных стержней):

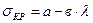
где a и b – эмпирические коэффициенты, имеющие размерность напряжения. Для чугунных стержней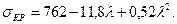

Эмпирические формулы Тетмайера – Ясинского применимы при

Где λ₀ – значение гибкости, при которой критическое напряжение становится равным пределу текучести (для стальных и дюралюминиевых стержней).

Для чугунных стержней условие применимости эмпирической формулы также выражается неравенством значения 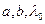и 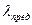приведены в таблице.

Материал	a Н/мм^2	b Н/мм^2	λ0	λпред
Сталь 10, Ст2………………………….. Сталь 15, Ст3………………………….. Сталь 25, Ст5………………………….. Сталь 10Г2СД, 15ГС…………………. Дюралюминий Д16Т…………………. Сосна, ель……………………………... Чугун…………………………………..	29,3 -	0,70 1,14 1,15 1,52 2,83 0,194 -	-

Стальные и деревянные стержни строительных конструкций, а также сжатые стержни металлоконструкций подъемно – транспортных машин рассчитывают по формуле

,

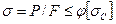где F – площадь поперечного сечения стержня; φ – коэффициент продольного изгиба; [σ_с] – основное допускаемое напряжение на сжатие, устанавливаемое без учета опасности продольного изгиба.

Коэффициент φ зависит от материала и гибкости стержня, Последняя при проектном расчете неизвестна, поэтому его приходится вести последовательными приближениями.

Задача 1

По расчетной схеме трубчатой стойки самолетной конструкции проверить устойчивость стойки при , если она изготовлена из хромоникелевой стали, для которой Е= 2,1·10⁵Н/мм² и σ_ПЦ=450Н/мм². Решение. Для расчета на устойчивость должна быть известна критическая сила для заданной стой-ки. Необходимо установить, по какой формуле сле-дует вычислять критическую силу, т.е. надо сопоста-вить гибкость стойки с предельной гибкостью для ее материала. Вычисляем величину предельной гибкости, так как табличных данных о λ_пред для материала стойки не имеется:

Р=100кН

d=40

l=1700

D=50

Для определения гибкости рассчитываемой стойки вычисляем геометрические характеристики ее поперечного сечения:

.

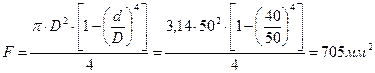
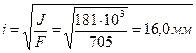Определим гибкость стойки:

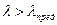и убеждаемся, что , т.е. критическую силу можно определить по формуле Эйлера:

Вычисляем расчетный (действительный) коэффициент запаса устойчивости:

Таким образом, 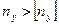на 5,2%

Задача 2

Определить допускаемую величину сжимающей силы для стойки, сваренной из двух швеллеров. Материал стойки – сталь Ст2, требуемый коэффициент запа-са устойчивости [n]=2,2. Как изменится величина [Р], если длину стойки уменьшить вдвое? Решение. Для определения допускаемой величины сжимающей силы надо знать величину критической силы. Чтобы установить, по какой формуле следует определять Р_КР, надо вычислить гибкость стойки. Отределяем главные центральные момен-

Р

Y Z₀

l=9м Х

№10 b

ты инерции сечения, принимая исходные геометрические характеристики по ГОСТ 8240-72;

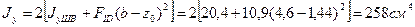
Таким образом, и

Площадь сечения

Минимальный радиус инерции

Гибкость стойки (при μ=0,5)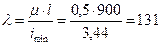

Следовательно, 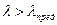и критическую силу определяем по формуле Эйлера:

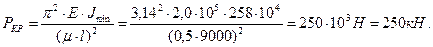
Величина допускаемой силы

При уменьшении длины стойки вдвое критическая (и допускаемая) сила увеличится не в четыре раза, как можно было бы ожидать исходя из формулы Эйлера, а меньше. Действительно, гибкость стойки уменьшенной длины

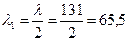т.е. , но , и критичкское напряжение (соответственно и критическую силу) следует определять по эмпирической формуле Тетмайера – Ясинского. Применим указанную формулу, беря значения коэффициентов из таблицы

.

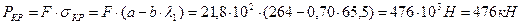Допускаемая сила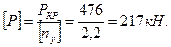

Таким образом, величина критической и допускаемой сил возросла лишь в 1,9 раза. Это пример подтверждения того, что нельзя применять формулу Эйлера при гибкости, меньшей предельной.

Определить величину допускаемой силы для чугунной стойки при [n_y]=5,0. Решение. Минимален момент инерции относительно оси у. J_min= 20³·30/12-16³·26/12= = 11,1·10³см⁴. Площадь сечения F=30·20-26·16=184 см². Минимальный радиус инерции Гибкость стойки при μ=1,0

Р Задача 3

Y 20

l=4,5м

200 20 Х

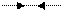
Так как λ<λ_пред, то для определения применим эмпирическую формулу

Определяем допускаемую нагрузку:

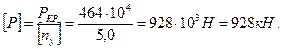
Дата добавления: 2015-06-30