Расчет балок из хрупких материалов

Построение эпюры. В произвольном сечении первого участка. В произвольном сечении второго участка. В произвольном сечении третьего участка. Под сосредоточенными силами на эпюре получаются скачки, равные по величине приложенным силам.

Пример 4.

Построить эпюры 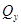и 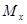для балки, изображённой на рисунке 2.6.7.

Р е ш е н и е. Определим опорные реакции:

; ; ;

; ; .

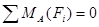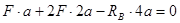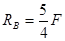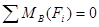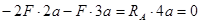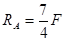Составляя сумму проекций на вертикальную ось всех сил, действующих на балку, получаем

,

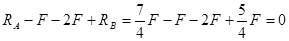следовательно, опорные реакции определены верно.

Балка имеет три участка нагружения. В пределах каждого участка отсутствует распределённая нагрузка, следовательно, в пределах каждого участка 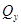= const, а 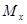изменяется по линейному закону.

Построение эпюры 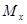. На первом участке изгибающий момент возрастает (на этом участке поперечная сила положительна) от нуля (в крайнем левом сечении отсутствует сосредоточенная пара сил) до 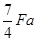. На втором участке изгибающий момент возрастает (на этом участке поперечная сила положительна) от 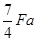до 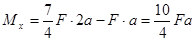. На третьем участке изгибающий момент убывает (на этом участке поперечная сила отрицательна) от 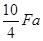до нуля (в крайнем правом сечении отсутствует сосредоточенная пара сил). Как видно из рисунка, под сосредоточенными силами на эпюре 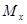получаются резкие изменения угла наклона (изломы) смежных участков эпюры.

2.6.4. Выше было установлено, что при поперечном прямом изги­бе в поперечных сечениях балки возникают нормальные и каса­тельные напряжения. В частном случае, когда поперечная сила равна нулю, имеет место чистый изгиб и в поперечных сеченияхбалки касательные напряжения отсутствуют. Этот случай рас­смотрим в первую очередь. Для выяснения закона распределе­ния нормальных напряжений по поперечному сечению балки и вывода формулы, определяющей напряжение в произвольной точке поперечного сечения, будем исходить из следующих допущений:

1. при чистом прямом изгибе справедлива гипотеза Бернулли, т. е. поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими инормальными к оси ипосле деформации;

2. продольные волокна бруса при его деформации не надавливают друг на друга, а испытывают только растяжение или сжатие.

Выделим из бруса (см. рис. 2.6.3.) двумя поперечными сечениями бесконечно малый элемент длиной dz (рис. 2.6.8.). Действие отброшенных частей балки заменяем изгибающими моментами 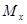. На рисунке 2.6.8, Бпоказан выделенный эле­мент после его деформации. Между растянутыми и сжатыми слоями расположен нейтральный слой .

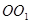Формула для определения нормальных напряжений в любой точке поперечного сечения бруса при чистом изгибе имеет вид

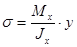. (2.6.2.)

Таким образом, нормальные напряжения в произвольной точке поперечного сечения прямо пропорциональны её расстоянию от нейтральной оси, т.е. по высоте сечения нормальные напряжения изменяются по линейному закону (рис. 2.6.8. Б). По ширине сечения они распределены равномерно (не зависят от координаты ).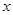

При вычислении 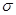значения 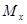и подставляют в формулу (2.6.2.) без учёта их знака. Как обычно, напряжения растяжения считаем положительными, а сжатия - отрицательными.

Возвращаясь к рис. 2.6.8.Б, заметим, что нейтральная ось (она принята за координатную ось) делит поперечное сечение бруса на две части, в одной из которых возникают растягивающие, а в другой – сжимающие напряжения. В точках, лежащих на самой нейтральной оси, нормальные напряжения равны нулю. Таким образом, наряду с определением нейтральной оси как линии пересечения нейтрального слоя с плоскостью поперечного сечения можно дать и другое: нейтральной осью или нулевой линией называется геометрическое место точек поперечного сечения бруса, в которых нормальные напряжения равны нулю.

Формула (2.6.2.) выводится для случая чистого прямого изгиба бруса. При поперечном прямом изгибе предпосылки, поло­женные в основу ее вывода, нарушаются: поперечные сечения бруса вследствие возникновения в них касательных напряжений искривляются (гипотеза Бернулли несправедлива); кроме того, в этом случае имеет место, хотя и весьма незначительное, взаимное надавливание волокон. Тем не менее, как показывают экспериментальные и точные теоретические исследования, эта формула дает значения нормальных напряжений и для случая поперечного изгиба с точностью, вполне достаточной для прак­тических расчетов.

Формулой (2.6.2.) можно пользоваться во всех случаях прямо­го изгиба, понимая под 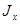момент инерции относительно главной цен­тральной оси поперечного сечения, перпендикулярной плоскости дей­ствия нагрузки.

2.6.5. Балки рассчитывают на прочность по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. При поперечном изгибе балок наряду с нормальными, как известно, возникают и касательные напряжения, но они в по­давляющем большинстве случаев невелики и при расчетах на прочность не учитываются. В коротких брусьях тонкостенного профиля (например, двутавров) или брусьях, нагруженных большими сосредоточенными силами близко от опор, касательные напряжения могут быть весьма значительными, поэтому для таких балок дополнительно к основному расчёту на прочность по нормальным напряжениям выполняют расчёт по касательным напряжениям.

Расчет балок из пластичных материалов. Прочность балки из пластичного материала обеспечена, если наибольшие по абсолютному значению нормальные напряже­ния, возникающие в опасном поперечном сечении, не превы­шают допускаемых. Для балки, поперечные размеры которой по всей длине постоянны (пока только такими балками и огра­ничимся), опасное сечение то, в котором возникает наибольший по модулю изгибающий момент.

Наибольшие нормальные напряжения возникают в точках (будем называть эти точки опасными) опасного поперечного сечения, максимально удаленных от нейтральной оси:

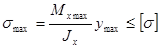. (2.6.3.)

Здесь [ 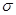] — допускаемое напряжение, принимаемое при ста­тическом нагружении таким же, как и в случае растяжения (сжатия) бруса из того же материала; - расстояние от опасной точки до нейтральной оси.

В случае если поперечное сечение балки симметрично отно­сительно нейтральной оси, оказывается возможным привести формулу (2.6.3.) к более удобному виду. Для указанных сечений 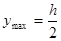, где h — высота сечения (размер в направлении, пер­пендикулярном нейтральной оси), следовательно,

.

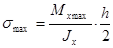Введем обозначение 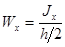и получим окончательное условие прочности в следующем виде:

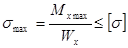. (2.6.4.)

Таким образом, введена новая геометрическая характери­стика поперечного сечения 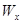, представляющая собой отноше­ние момента инерции относительно данной оси к половине вы­соты сечения. Эту геометрическую характеристику называют осевым моментом сопротивления. Момент сопротивления имеет размерность м³.

Из формулы (2.6.4.) следует, что момент сопротивления - это геометрическая характеристика прочности бруса, работающего на прямой изгиб. Действительно, чем больше момент сопро­тивления, тем меньше напряжения, возникающие в поперечном сечении балки при данной нагрузке (изгибающем моменте), и тем большую нагрузку может безопасно выдержать балка при данном значении допускаемого напряжения (при данном материале).

Значения осевых моментов сопротивления прокатных профилей (двутавров и швеллеров) приведены в таблицах соответствую­щих ГОСТов.

Моменты сопротивления круга, кольца и прямоугольника найдем, воспользовавшись формулами для главных цен­тральных моментов инерции этих сечений:

Для кольцевого сечения:

, .

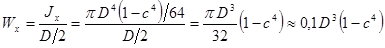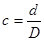Для круглого сплошного сечения:

.

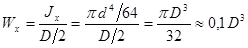Для прямоугольного сечения:

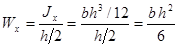. (2.6.5.)

Во избежание ошибок еще раз подчеркиваем, что в формуле (2.6.5.) h — сторона прямоугольника, перпендикулярная оси, от­носительно которой вычисляется момент сопротивления.

При применении для балок из пластичных материалов сече­ний, симметричных относительно нейтральной оси, обеспечи­вается равенство наибольших растягивающих и сжимающих напряжений (рис.2.6.9.). Для указанных материалов это, конеч­но, целесообразно, так как допускаемые напряжения на растя­жение и сжатие для них одинаковы.

Нетрудно понять, что не все симметричные сечения одина­ково рациональны. Действительно, распределение нормальных напряжений таково, что та часть материала, которая располо­жена вблизи нейтральной оси, почти не используется. Это указывает, в частности, на нерациональность круглого сече­ния — при его применении большая часть материала бруса оказывается в мало нагруженной области. Не­многим выгоднее квадратное сечение. Наилучшее решение вопроса о рациональном использовании материала дает применение двутаврового сечения. В двутавровой балке основная часть материала сосредоточена в полках, т. е. в зоне наилучшего его использования (в зоне наибольших напряжений). Роль стенки балки, воспринимающей сравнительно не большую часть изгибающего момента, состоит в обеспечении монолитной работы сечения как единого целого.

Поскольку момент сопротивления является геометрической характеристикой прочности изгибаемого бруса, очевидно, следует стремиться к тому, чтобы при данной затрате материала он был максимален. При заданной длине балки затрата материала (масса балки) прямо пропорциональна площади поперечного сечения. Следовательно, чем больше 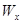и меньше А, тем рациональнее форма сечения балки.

Необходимо иметь в виду, что при изменении положения сечения по отношению к действующей нагрузке прочность бал­ки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для бруса прямоугольного сечения с отношением сторон 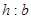= 3, расположенного, как показано на рис. 2.6.10. А, допускаемая нагрузка в три раза больше, чем для того же бруса, но повернутого на 90° (рис. 2.6.10.Б). Анало­гично для двутавра № 20а, показанного на рис. 2.6.11.А, допу­скается нагрузка больше, чем для показанного на рис. 2.6.11.Б, в 7,2 раза.

Из приведенных примеров следует, что сечение надо распо­лагать таким образом, чтобы силовая линия совпадала с той из главных осей, относи­тельно которой момент инерции минимален, или, что то же самое, так, что­бы ось, относительно ко­торой момент инерции максимален, была нейт­ральной осью сечения. Более кратко это указа­ние можно сформулиро­вать так: следует стремиться к тому, чтобы изгиб бруса происходил в плоскости его наиболь­шей жесткости.

Вбольшинстве случаев с увеличением момента инерции се­чения возрастает и его момент сопротивления, но возможны и исключения, когда нерациональное увеличение момента инер­ции приводит к уменьшению момента сопротивления, т. е. к снижению прочности бруса. Один из подобных примеров приведен на рис. 2.6.12.: приварка полос к двутавру приводит к уменьшению 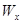, так как высота сечения возрастает ощути­мее, чем его момент инерции.

Хрупкие материалы применяют для изготовления некоторых работающих на изгиб элементов машиностроительных конструкций. В частности, из серого чугуна отливают различного рода рамы, станины, подшипниковые подвески и т. д.

Как известно, серый чугун работает на сжатие значительно лучше, чем на растяжение; отношение соответствующих допускаемых напряжений

.

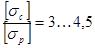Очевидно, применение сечений, симметричных относительно нейтральной оси, в рассматриваемом случае нерационально - материал в сжатой зоне бруса будет значительно недогружен, что приведет к его излишней затрате, а значит, к увеличении массы конструкции.

Для балок из хрупких материалов, различно сопротивляющихся растяжению исжатию, целесообразно применять сечения несимметричные относительно нейтральной оси, например тавровое, несимметричное двутавровое, П-образное (рис. 2.6.13.). При этом целесообразно располагать сечение таким образом, чтобы большая часть балки находилась в растянутой зоне (см. эпюр; нормальных напряжений на рис. 2.6.13.), при этом растянутые волокна оказываются приближенными к центру тяжести сечения.

Очевидно, следует стремиться к тому, чтобы максимальны растягивающие и максимальные сжимающие напряжена в опасном поперечном сечении балки были одновременно равны соответствующим допускаемым напряжениям, т.е.

, .

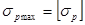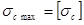При этом материал балки используется наиболее рационально. Но

, ,

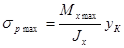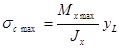где 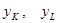- расстояния от нейтральной оси соответственно до наиболее удалённых точек растянутой и сжатой зон сечения (рис. 2.6.13.). Следовательно, для обеспечения указанного условия наиболее рационального использования материала сечение должно иметь такую конфигурацию, при которой

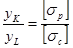. (2.6.6.)

Соотношение (2.6.6.) выполняется далеко не всегда, поэтому условие прочности чугунной балки выражается двумя неравенствами:

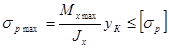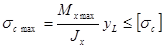, . (2.6.7.)

Если 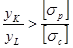, опасными являются точки растянутой зоны, максимально удалённые от нейтральной оси, и для расчёта на прочность достаточно использовать только первую из формул (2.6.7.). Аналогично, при 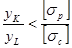достаточно выполнить расчёт по второй из формул (2.6.7.).

Всё сказанное о расчёте чугунной балки относилось в основном к случаю, когда эпюра изгибающих моментов на всём протяжении однозначна. В случае если эпюра 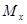имеет участки разных знаков (например, рис. 2.6.14.), следует расположить сечение таким образом, чтобы там, где изгибающий момент по абсолютному значению максимален (сечение 1-1), большая часть материала (например, полка таврового сечения) находилась в растянутой зоне. При этом помимо расчёта на прочность для указанного сечения, необходимо произвести расчёт по максимальным растягивающим напряжениям для сечения с наибольшим моментом противоположного знака (сечение 2-2). Здесь хотя изгибающий момент и меньше, но большая часть материала находится в сжатой зоне и может оказаться, что именно это сечение является опасным.

2.6.6. В ряде случаев работающие на изгиб элементы машино­строительных и строительных конструкций должны быть рас­считаны не только на прочность, но и на жесткость. К деталям, рассчитываемым на жесткость, относятся, в частности, валы зубчатых и червячных передач и многие части металлорежущих станков.

Как известно из предыдущего, расчет на жесткость элемен­та конструкции, имеющего форму бруса, заключается в опреде­лении наибольших перемещений его поперечных сечений и со­поставлении их с допускаемыми, зависящими от назначения иусловий эксплуатации данного элемента. Например, рас­считывая вал на жесткость при кручении, ограничивают углы поворота поперечных сечений вокруг его продольной оси.

Расчет на жесткость при изгибе, очевидно, требует предва­рительного изучения вопроса о перемещениях поперечных сече­ний балок.

Рассмотрим простую консоль, нагруженную на свободном конце силой F, линия действия которой совпадает с одной из главных осей поперечного сечения балки (рис. 2.6.15.).

При деформации балки центры тяжести ее поперечных сече­ний получают линейные перемещения, а сами сечения повора­чиваются вокруг своих нейтральных осей. Допущение о мало­сти перемещений позволяет считать, что направления линейных перемещений перпендикулярны продольной оси недеформированного бруса. Эти перемещения принято называть прогибами. Прогиб произвольного сечения обозначим 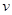, а наибольший прогиб — стрелу прогиба — 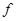. Геометрическое место центров тяжести поперечных сечений деформированного бруса, т. е. ось изогнутого бруса, условно называют изогнутой осью или чаще упругой линией. Эта линия — плоская кривая, лежащая в сило­вой плоскости. Совпадение плоскости деформации с плоскостью действия нагрузки является характерной особенностью прямого изгиба. Более того, можно сказать, что именно по этой причине рассматриваемый случай изгиба называют прямым.

При повороте поперечные сечения остаются перпендику­лярными изогнутой оси бруса, что следует из справедливости гипотезы Бернулли.

Следовательно, угол (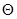) поворота поперечного сечения равен углу между касательной к упругой линии в данной точке и осью недеформированного бруса.

Для вычисления перемещения с помощью интеграла Мора нужно выполнить следующие операции:

1) составить уравнение изгибающих моментов 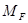от за­данной нагрузки;

2) освободив систему (балку) от заданной нагрузки, прило­жить к ней силу, равную единице в той точке, где определяется перемещение, и по направлению этого перемещения;

3) составить уравнение изгибающих моментов 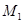от этой единичной силы;

4) вычислить сумму интегралов от произведения обо­их моментов, деленного на жесткость сечения:

.

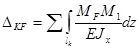Если определению подлежит не прогиб, а угол поворота ка­кого-либо поперечного сечения, то к разгруженной балке сле­дует приложить в этом сечении не силу, а пару сил с моментом, равным безразмерной единице (сокращенно — единичный мо­мент). В остальном техника определения перемещений не изменяется.

Так же как при определении прогибов, направления поворо­та сечения и приложенного единичного момента совпадают, ес­ли результат вычисления интеграла Мора получается со зна­ком плюс.

Расчёт бруса на жёсткость при изгибе заключается в определении наибольших перемещений его поперечных сечений и сравнении их с допускаемыми по условиям эксплуатации, так же как при растяжении и кручении. Зачастую оказывается, что требуемые размеры поперечного сечения бруса, определяемые из расчёта на жёсткость, получаются большими, чем требуемые по условию прочности.

В большинстве случаев условие жесткости выражается нера­венством

,

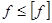т. е. максимальный прогиб (стрела прогиба 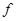) не должен пре­вышать допускаемого 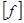. Значение допускаемого прогиба за­висит от назначения и условий работы рассчитываемой кон­струкции и колеблется в широких пределах.

Обычно допускае­мую стрелу прогиба указывают в долях пролета (межопорного расстояния 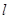) балки. Например, для ручных грузоподъемных кранов 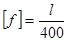, то же, электрических 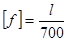; для валов и шпинделей металлорежущих станков 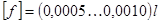. Для обеспечения нормальной работы подшипников сколь­жения и роликовых подшипников качения иногда ставится до­полнительное условие жесткости — ограничение угла поворота опорных сечений:

.

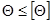При этом допускаемый угол поворота составляет в среднем 0,001 рад.

В тех случаях, когда конструктивные и технологические тре­бования не накладывают особых ограничений на форму попе­речных сечений проектируемого элемента конструкции, следует применять такие сечения, которые обеспечивали бы возможно большую жесткость при наименьшем расходе материала. Жесткость балки прямо пропорциональна моменту инерции 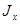ее поперечного сечения относительно нейтральной оси, а рас­ход материала (масса балки) прямо пропорционален площа­ди сечения А. Для оценки рациональности формы попереч­ного сечения балки, размеры которой определяются из расчета на жесткость, удобна безразмерная характеристика ^.

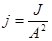Например, для двутавра № 20 (при изгибе в плоскости на­ибольшей жесткости) 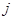= 2,56; для того же двутавра при изгибе в плоскости наименьшей жесткости 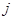= 0,161; для круга 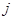= 0,0795; для квадрата 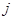= 0,0834; для кольца (при с = 0,7) 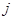= 0,232.

2.6.8. В поперечных сечениях балок, как было установлено выше, при чистом изгибе возникают только нормальные, а при попе­речном изгибе - как нормальные, так и касательные напря­жения.

Из закона парности касательных напряжений следует, что в продольных сечениях балки, параллельных нейтральному слою, также возникают каса­тельные напряжения (рис. 2.6.16.). Для данной точки балки каса­тельное напряжение 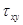, возни­кающее на площадке попереч­ного сечения, равно касатель­ному напряжению 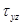, возни­кающему на площадке продольного сечения, проведенного через ту же точку.

Наличие касательных напряжений в продольных сечениях балок подтверждается также и результатами следующего про­стого опыта. Представим себе две одинаково нагруженные двухопорные балки (рис. 2.6.17.), одна из которых состоит из ря­да отдельных положенных друг на друга и ничем не скре­пленных брусьев. Каждый из этих брусьев деформируется неза­висимо от других (влияние сил трения между брусьями не учитываем), имея собственный нейтральный слой. В результате деформации отдельные брусья, составляющие балку, взаимно сдвинутся. В целой балке взаимного сдвига ее продольных слоев не происходит; это и указывает на наличие в продольных плоскостях касательных напряжений, препятствующих этим сдвигам. Попутно заметим, что прогибы целой балки будут значительно меньше, чем балки, состоящей из отдельных брусьев.

В балке прямоугольного сечения максимальные касатель­ные напряжения возникают в тех точках, где нормальные напряжения равны нулю (на нейтраль­ной оси), и, наоборот, в крайних точках сечения, где нормальные на­пряжения максимальны, касательные напряжения равны нулю. Сказанное справедливо также для балок круг­лого сечения.

В прокатной или сварной двутавровой балке, имеющей сравнительно большую высоту, касательные напряжения могут быть значительны при условии, что балка нагружена больши­ми сосредоточенными силами и длина ее невелика или эти силы приложены близко к опорам. В этом случае помимо ос­новного расчета на прочность по нормальным напряжениям следует проверить максимальные касательные напряжения в том сечении, где поперечная сила имеет наибольшее значение. Обычно принимают (для стальных балок) .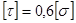

Дата добавления: 2015-06-30