Обслуживание потока от ограниченного числа источников нагрузки. Вывод формулы Энгсета

ПЕРВАЯ ФОРМУЛА ЭРЛАНГА.

1. Первая формула Эрланга

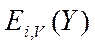- используется интенсивность поступающей нагрузки.

Если V→∞, то распределение Эрланга переходит в распределение Пуассона:

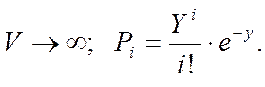
1-я ф-ла Эрланга справедлива при любом распределении длительности обслуживания, лишь бы поступивший на вход КС поток был простейшим.

Постановка задачи:

1. Определим 3 основных элемента математической модели:

а) структура коммутационной системы однозвенная в выходы включен полнодоступный пучок емкостью V.

б) входные/выходные потоки - на входы КС поступает случайный ординарный поток вызовов от N источников, вероятность поступления новых вызовов в систему зависит от числа обсуживаемых в рассматриваемый момент. Такой поток называется примитивным и параметр λ_i=α(N-i). α – параметр (интенсивность) потока вызовов от 1 свободного источника, функция распределения: , длительность обслуживания подчиняется экспоненциальному закону: 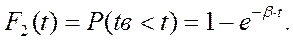tв – длительность обслуживания.

в) дисциплина обслуживания с явными потерями, т.е. если вызов получает отказ в обслуживании он теряется и не оказывает влияния на систему в дальнейшем.

Математическая модель:

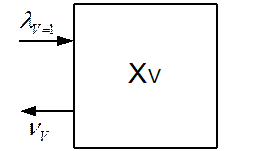Необходимо найти вероятность занятия любых i линий из V в фиксированные моменты времени.

Пусть α – параметр свободного источника, т.е. вероятность поступления хотя бы одного вызова на промежутке Δt→0. В состоянии Xi из N источников свободно N-i, тогда вероятность поступления вызовов, если система находится в состоянии Xi м.б. записана ,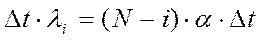

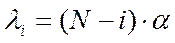. Вероятность того, что произойдет освобождение 1 линии и система перейдет в состояние Xi-1: 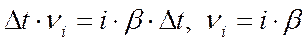. Подставляя в формулу для Pi, получим:

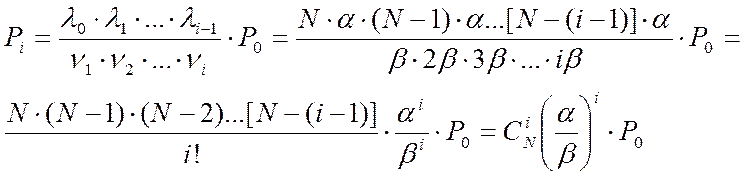
В теории массового обслуживания очень часто длительность занятия обслуживающего устройства выражается в единицах средней длительности одного занятия:

, тогда .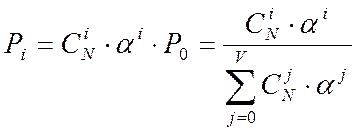

Распределение Энгсета – дает вероятность занятия одной линии из V при поступл. на вход однозв. полнодоступной КС ординарного стационарного потока от ограниченного числа источников нагрузки.

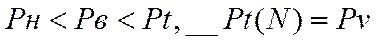- вер-ть того, что заняты все лини.

11. Сравнение пропускной способности полнодоступного пучка, об­служивающего вызовы примитивного и простейшего потоков.

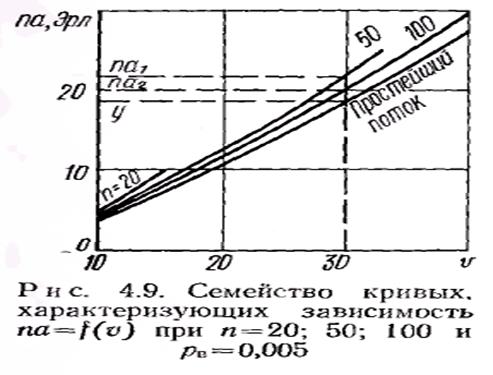
Полнодоступный пучок емкостью u(1£u<¥) линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, которые образуют примитивный поток с параметром l _i.. 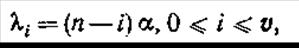Ха­рактер зависимости величины поступающей нагрузки па от емко­сти пучка линий v, который обслуживает вызовы примитивного по­тока, поступающие от фиксированного числа источников п, такой же, как и при обслуживании вызовов простейшего потока. Однако нa пропускную способность пучка вли-1ет число источников вызовов п: в области малых потерь с уменьшением п увеличивается пропускная способность пучка. Это иллюстрируется семейст­вом кривых У= na=f(u) при р_в = 0,005, приведенном на рис. 4.9. Эти кривые одновременно показывают, что при за­данном качестве обслуживания посту­пающая на v линий пучка нагрузка па, создаваемая вызовами примитивного потока от любого числа источников, имеет большую величину по сравнению с нагрузкой у, создаваемой вызовами простейшего потока. Так, при v = 30 нагрузки, поступающие от «i = 50 и n2 = 100, могут достигать соответствен­но значений na1 = 21,65 Эрл и na₂ = 20 Эрл, а нагрузка, которая соз­дается вызовами простейшего потока, у=18,7 Эрл, т. е. нагрузка от п=50 на 8,2% больше нагрузки, поступающей от n=100, и на 16% больше нагрузки, создаваемой вызовами простейшего потока. Заметим, что с увеличением потерь р_ъ: а) существенно умень­шается влияние п на пропускную способность пучка; б) сокраща­ется различие между пропускной способностью пучков, обслужи­вающих вызовы примитивного и простейшего потоков. В то же время нагрузка па₀, обслуживаемая полнодоступным пучком v в области любых потерь, выше при обслуживании вызовов прими­тивного потока (па₀=па(1 —р_н)), а р_н всегда меньше E_v(na). Так, например, обслуженная нагрузка, создаваемая примитивным пото­ком от n=50, при p_H=E_v(na)=0.01 на 12% и при р_н =E_v(na) = = 0,2 на 6% выше обслуженной нагрузки, создаваемой простей­шим потоком вызовов. Таким образом, с точки зрения величины обслуживаемой нагрузки примитивный поток всегда «лучше» про­стейшего потока вызовов.

Дата добавления: 2015-06-30