Системы с ожиданием при постоянной длительности занятия

Математическая модель таких систем записывается в следующем виде M|D|V|r=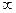

Пуассоновский поток (нагр.) на входе.

V-кол-во обслуживаемых приборов

R – время ожидания

D – дисциплина обслуживания. Длительность.

К таким системам (длит. занятия const) может быть отнесены управляющие устройства, координатные и квазиэлектронные АТС.

Существуют две математические модели для таких систем:

- модель Кроммелина

- модель Берке

Основное отличие этих моделей от модели Эрланга:

1) здесь рассматривается только постоянная длительность обслуживания (h)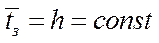

2) в модели Кроммелина рассматривается обслуживание вызовов в порядке из поступления, также предполагается, что все поступившие вызовы будут обслужены, т.е. Y=Y_О.

3) И были получены графические зависимости 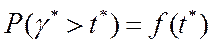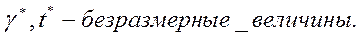для различных значений 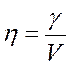нагрузка на один обслуживаемый прибор или на одну линию. ,

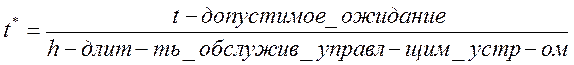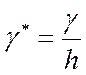
4) модель Кроммелина существует как для однолинейных систем V=1, так и для многолинейных V 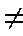1.

Модель Берке отличает от м. Кроммелина тем, что в м.Б. рассматривается случайный выбор вызовов из очереди.

Если сравнить кривые Кроммелина и Берке, то…

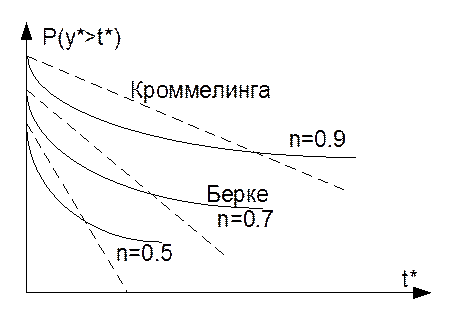
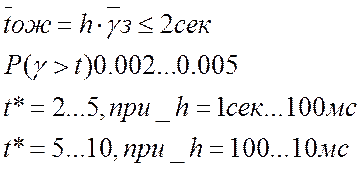Если рассмотреть механические АТС и механико-электрические АТС, то длительность занятия h для таких управляющих устройств находятся в диапазоне 10мс – 1с

Для цифровых систем коммутации в случае программного управления длительность занятия управляющих устройств составляет менее 5мс. Это позволяет допускать величину t^* до 100 и более единиц.

Управляющие устройства, как правило, обслуживают вызовы с ожиданием со случайным выбором из очереди. Если считать поступающий поток простейшим, длит-ть работы управл устройства – постоянной, то модель Берке наиболее близка к условиям работы одного управляющего устройства. Если обслуживание осуществляется несколькими управл устройствами, то использ-ся многолинейная модель Кроммелина.

15. Упрощенные методы расчета пропускной способности НПД схем (Эрланга, О’Делла, Пальма-Якобеуса)

Неполнодоступным (НПД) включением называется такое включение линий рассматриваемого пучка, при котором каждому входу коммутационной схемы доступна лишь часть линий пучка. Доступностью НПД пучка линий называется число линий, доступных каждому входу ступени искания. Обозначается D.

Необходимость образования НПД включений вызвана конструктивными ограничениями коммутационных приборов и, стремлением повысить использование линий в пучке.

Совокупность входов коммутационной схемы, каждый из которых доступен одним и тем же D линиям пучка, называется нагрузочной группой. Число нагрузочных групп обозначается через g.

Необходимым условием НПД включения является неравенство .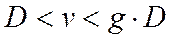

Отношение 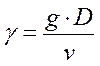, называется коэффициентом уплотнения и характеризует среднее число нагрузочных групп, доступных одной линии пучка.

Коэффициент уплотнения находится в пределах . В большинстве практических случаев оптимальное значение j находится в пределах от 2 до 4.

Число связей между выходами отдельных нагрузочных групп обычно записывается в виде матрицы связности. Диагональный элемент матрицы равен доступности схемы. Каждый элемент матрицы 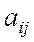показывает число связей между i и j нагрузочными группами.

НПД включение будет оптимальным, если элементы внутри матрицы не будут отличаться более чем на единицу, а сумма по строке должна быть одинаковой или отличаться не более, чем на единицу.

Для практических расчетов пропускной способности однозвенных неполнодоступных коммутационных схем используют приближенные методы.

Упрощенная формула Эрланга: 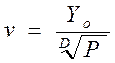, где Y₀ - интенсивность обслуженной пучком линий нагрузки; Р - вероятность потерь; D - доступность; 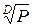- средняя пропускная способность одной линии пучка.

Формула 0`Делла: 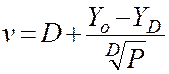, где 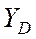- нагрузка, обслуженная полнодоступным пучком из D линий при потерях Р и приблизительно определяемая с помощью 1-й формулы Эрланга (по таблицам Пальма). При отсутствии таблиц можно использовать рекуррентные соотношения:

или

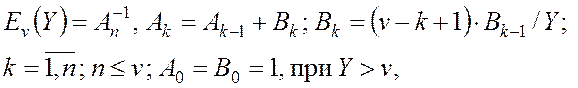
где Y – интенсивность поступающей нагрузки.

Формула Пальма-Якобеуса: 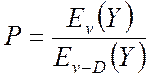, где Y - интенсивность поступающей на пучок линий нагрузки.

В модифицированной формуле Пальма-Якобеуса вместо поступающей нагрузки Y в формулу Пальма-Якобеуса подставляется значение фиктивной нагрузки Y_ф, определяемой из выражения

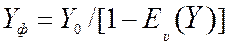, где .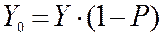

При малых значениях потерь Р можно считать Y=Y₀. Поэтому все эти формулы при фиксированных D и Р могут быть приведены к виду; 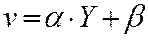, где значения a и b зависят от D и Р.

Для упрощенной формулы Эрланга: ;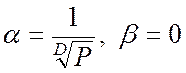

для формулы 0'Делла: ;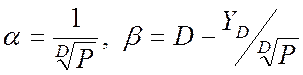

для формулы Пальма-Якобеуса эти коэффициенты можно подобрать. Значения a и b для формулы О'Делла табулированы и для некоторых значений Р и D приведены в табл. П2.

Дата добавления: 2015-06-30