Минимизация при помощи карт Карно

Минимизация на основе использования законов алгебры логики

Минимизация полностью заданных ФАЛ

При минимизации ФАЛ с использованием законов булевой алгебры, функция должна быть представлена в аналитическом виде.

Для получения минимальной ФАЛ пользуются аксиомами и законами АЛ, которые позволяют упростить исходное выражение (приложение В).

Например, для упрощения первой функции применяются распределительный закон, законы дополнительности и нулевого множества.

.

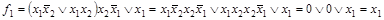Для упрощения второй функциииспользуют закон двойственности (правило де Моргана), распределительный закон, законы дополнительности и поглощения.

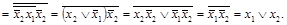
Функция представляется при помощи карты Карно. При этом для любой клетки карты существует соседняя по строке и столбцу, такая что координаты этой клетки отличаются от координат рассматриваемой клетки значением лишь одной переменной. Это свойство позволяет выполнять на карте минимизацию функций, отображая процесс склеивания соседних конституентов и минтермов, соответствующих клеткам карты, путем построения различных объединений клеток.

Минимальные выражения могут быть получены как на основе ДНФ, так и на основе КНФ. Если требуется получить выражение на базе ДНФ, то в карте учитываются клетки с единицами, а если на основе КНФ, то – с нулями.

Правила объединения в контуры при минимизации для ДНФ:

1) все единицы должны быть заключены в прямоугольные контуры;

2) во всех клетках контура должны быть только единицы;

3) число клеток в контуре должно быть кратным степени числа два (1, 2, 4, 8, 16, 32);

4) контуры могут накладываться друг на друга;

5) контуры, все клетки которых уже вошли в другие контуры, являются лишними;

6) для получения наиболее простой формулы надо выбирать контуры с максимально возможным числом клеток;

7) каждому контуру соответствует конъюнкция, составленная из переменных, значения которых не изменяются во всех клетках контура, т.е. конъюнкций будет столько, сколько в карте контуров.

При составлении конъюнкций контуров для каждого контура рассматривается вхождение всех аргументов.

Если контур пересекает (захватывает) как прямое, так и инверсное значение аргумента, то этот аргумент в конъюнкцию не входит.

Если же контур захватывает только прямое или только инверсное значение аргумента, то аргумент или его инверсия входит в конъюнкцию (значение, которое захватывается контуром и входит в конъюнкцию).

После получения конъюнкций для всех контуров эти конъюнкции объединяются друг с другом знаком дизъюнкции. В результате получается выражение минимизированной ФАЛ.

Рассмотрим некоторые примеры.

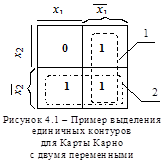На карте, показанной на рисунке 4.1, удалось выделить два контура. Это значит, что в упрощенном выражении должно быть две элементарные конъюнкции. Для контура, обозначенного цифрой 1, в конъюнкции будет отсутствовать переменная 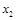, так как она входит в первый контур прямым и инверсным значением, и останется лишь переменная . Для контура, обозначенного цифрой 2, в конъюнкции будет отсутствовать переменная 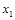по той же причине, а в конъюнкции останется 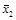, так как захватывается только инверсное значение переменной. Объединив полученные конъюнкции для обоих контуров знаками дизъюнкции, получим выражение упрощенной функции .

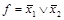На карте Карно, представленной на рисунке 4.2, получено три контура.

Клетки карты, которые при ее условном «сворачивании» могут образовывать прямоугольные контуры с числом клеток кратным степени числа два, также могут объединяться в контуры. Примером такого объединения является контур под номером 3.

Упрощенная функция будет иметь три конъюнкции, соответственно числу контуров. При этом в конъюнкции для 1-го контура будет отсутствовать переменная х ₃, в конъюнкции для 2-го контура – переменная х ₂, а в конъюнкции для 3-го контура – переменная х ₁. Получим упрощенную функцию
.

На карте, представленной на рисунке 4.3, выделено четыре контура. При этом контур 3 образован при условном «сворачивании» карты Карно в «цилиндр» в горизонтальной плоскости, а контур 4 – при «сворачивании» карты в «шар». Функция состоит из суммы четырех элементарных конъюнкций .

Наиболее часто карты Карно используются для упрощения ФАЛ от двух, трех и четырех переменных. Однако существует возможность использовать карты Карно для упрощения функций от пяти и шести переменных.

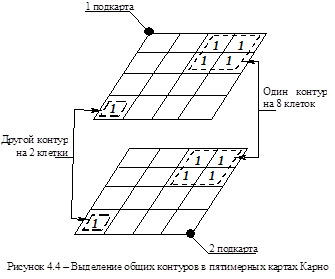
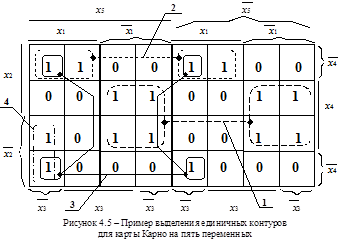
Правила минимизации такие же, как и для 2 – 4-х переменных. Однако правила объединения в контуры имеют дополнение для того случая, когда контуры выделяются в обеих подкартах. В один и тот же контур в разных подкартах могут объединяться только те клетки или их группы, которые располагаются точно друг над другом, если подкарты мысленно расположить одну над другой (рисунок 4.4). Так, для карты, представленной на рисунке 4.5, получаем четыре контура и следующую формулу упрощенной функции алгебры логики .

Правила объединения в контуры при минимизации для КНФ:

1) все нули должны быть заключены в прямоугольные контуры;

2) во всех клетках контура должны быть нули;

3) число клеток в контуре должно быть кратным степени числа два (1, 2, 4, 8, 16, 32);

4) контуры могут накладываться друг на друга;

5) контуры, все клетки которых уже вошли в другие контуры, являются лишними;

6) для получения наиболее простой формулы надо выбирать контуры с максимально возможным числом клеток;

7) каждому контуру соответствует скобочное выражение (скобка), состоящее из дизъюнкции переменных, значения которых не изменяются во всех клетках контура, т.е. скобок будет столько, сколько в карте контуров.

При составлении внутрискобочных дизъюнкций для каждого контура последовательно рассматривается вхождение всех переменных.

Если контур захватывает как прямое, так и инверсное значение аргумента, то этот аргумент в скобочную дизъюнкцию не входит. В том случае, если контур захватывает только инверсное или только прямое значение аргумента, то аргумент или его инверсия входит в дизъюнкцию.

Все полученные скобки объединяются между собой знаками конъюнкции. Это и будет минимальная ФАЛ. Причем, в отличие от случая с единицами, если аргумент входит в контур без инверсии, то в скобке он должен ставиться с инверсией и наоборот.

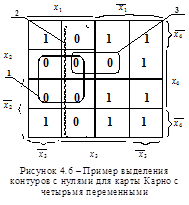Рассмотрим пример на карте Карно для четырех переменных для той же функции, которая была представлена на рисунке 4.3. Выделение контуров с нулями представлено на рисунке 4.6. Для рассматриваемого рисунка получаем три контура с нулями, которым соответствуют три скобочные дизъюнкци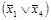и , и 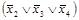. Объединив полученные скобки знаками конъюнкции, получаем формулу упрощенной ФАЛ на основе КНФ .

Проверка правильности полученных при минимизации функций осуществляется путем подстановки в полученную функцию всех наборов аргументов и сравнения ТИ для неупрощенной и упрощенной ФАЛ.

Наиболее часто карты Карно используются для упрощения ФАЛ от двух, трех и четырех переменных. Однако существует возможность использовать каты Карно для минимизации ФАЛ от пяти и шести аргументов.

Метод карт Карно при минимизации неудобен тем, что его трудно запрограммировать на ЭВМ, так как отсутствует четкий алгоритм его реализации и необходим нестандартный подход.

В результате упрощения методом карт Карно может быть получена ТДНФ (трудно поддающаяся дальнейшему упрощению) либо окончательно минимальная форма ФАЛ.

Дата добавления: 2015-07-02