Минимизация методом существенных переменных

Метод существенных переменных основан на сопоставлении разрешенных наборов значений переменных, на которых ФАЛ принимает единичное значение, с запрещенными наборами, на которых ФАЛ принимает нулевое значение. В том случае, если хотя бы на одном наборе переменных выполняется неравенство , переменная x _i является существенной. При минимизации неполностью заданных функций методом существенных переменных необходимо пройти следующие пять этапов [1].

1-й этап. Построение таблицы существенных переменных. Таблица должна содержать n строк – по числу разрешенных наборов функции, m столбцов – по числу запрещенных наборов и столбец остатков, в который записываются существенные переменные по результатам сравнения разрешенных наборов строк с запрещенными наборами столбцов.

2-й этап. Заполнение таблицы существенных переменных. Для этого попарно сравнивают разрешенный набор строки с каждым запрещенным набором столбца. В клетку таблицы заносятся те переменные, по которым рассматриваемая пара наборов различается между собой, и с теми значениями, которые переменные имеют в разрешенном наборе.

3-й этап. Обработка таблицы существенных переменных. Она проводится построчно в следующем порядке:

а) определяются те клетки, которые содержат по одной переменной. Эти переменные обводятся кружком и записываются в столбец остатков в виде конъюнкции. Все члены строки, которые содержат переменные, записанные в столбец остатков, отмечаются знаком дизъюнкции «Ú» и исключаются из рассмотрения;

б) среди членов строки, не отмеченных знаком «Ú», выделяется переменная, встречающаяся наиболее часто. Она обводится кружком и приписывается со знаком конъюнкции в столбец остатков к имеющимся там переменным. Члены строки, содержащие данную переменную, отмечаются знаком «Ú» и исключаются из рассмотрения. Этот процесс продолжается до тех пор, пока в строке останутся неотмеченными только клетки, содержащие неповторяющиеся переменные или переменные, повторяющиеся одинаковое число раз;

в) оставшиеся неотмеченными неповторяющиеся переменные или повторяющиеся одинаковое число раз соединяются знаком дизъюнкции, заключаются в скобки и через знак конъюнкции приписываются в столбец остатков к имеющимся там существенным переменным.

4-й этап. Построение таблицы покрытий существенных переменных. Эта таблица аналогична импликантной таблице в методе Квайна. Ее столбцы соответствуют разрешенным наборам, а строки – конъюнкциям существенных переменных, полученных для каждой строки таблицы существенных переменных. Если одним из членов конъюнкции в столбце остатков является дизъюнкция переменных, то осуществляется преобразование по распределительному закону (раскрываются скобки).

5-й этап. Обработка таблицы покрытий. Обработка выполняется, как и обработка импликантной таблицы: проставляются отметки в тех столбцах таблицы, наборы которых покрываются данной комбинацией существенных переменных, т.е. эта комбинация образована в результате сравнения соответствующего разрешенного набора с запрещенными наборами.

Этот метод минимизации следует использовать при большом числе переменных.

Рассмотрим реализацию данного метода на конкретном примере. Пусть неполностью определенная функция задана таблицей 4.9.

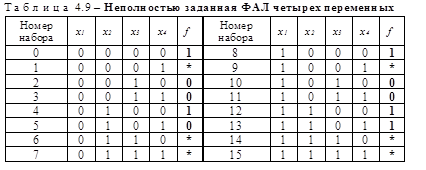
Анализируя данные таблицы, определяем, что в ней имеется 5 разрешенных (0, 4, 8, 12 и 13) наборов и 5 запрещенных (2, 3, 5, 10 и 11). Остальные наборы являются неиспользуемыми.

1-й этап. Составим таблицу существенных переменных (таблица 4.10).

Т а б л и ц а 4.10 – Таблица существенных переменных

Разрешенные наборы	Запрещенные наборы	Остатки

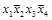
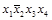
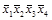
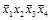
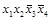
2-й этап. Заполним таблицу существенных переменных (таблица 4.11). Для этого поочередно сравним разрешенный набор каждой строки со всеми запрещенными наборами. В клетках на пересечении разрешенного и запрещенного наборов записываем несовпадающие элементы в таком виде, как они представлены в разрешенном наборе.

Т а б л и ц а 4.11 – Заполненная таблица существенных переменных

Разрешенные наборы	Запрещенные наборы	Остатки

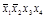
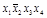
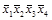
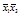
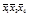
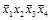
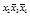
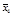
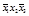
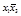
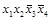
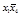
3-й этап. Обрабатываем таблицу существенных переменных (таблица 4.12). Определяем клетки, содержащие по одной переменной, обводим их кружком и записываем в столбец остатков. Отмечаем знаком «Ú» те члены строки, в которые входят обведенные кружком переменные, и исключаем их из дальнейшего рассмотрения.

Т а б л и ц а 4.12 – Заполненная таблица существенных переменных

Разрешенные наборы	Запрещенные наборы	Остатки
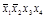
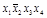
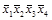
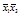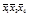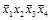
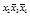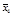
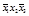
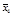
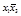		Ú		Ú	Ú
		Ú			Ú
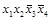
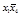
	Ú	Ú			Ú
	Ú	Ú

Среди членов строк, не отмеченных знаком «Ú», выделяем наиболее часто встречающуюся переменную, обводим ее кружком и дописываем со знаком конъюнкции в столбец остатков (таблица 4.13). Члены строки с выделенной переменной отмечаем знаком «Ú» и исключаем из рассмотрения.

Т а б л и ц а 4.13 – Заполненная таблица существенных переменных

Разрешенные наборы	Запрещенные наборы	Остатки
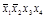
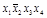
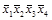
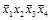
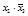
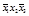				Ú
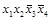
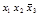
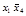
		Ú		Ú	Ú
				Ú

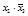
Оставшиеся неотмеченными неповторяющиеся переменные объединяем знаками дизъюнкции, заключаем в скобки и через знак конъюнкции дописываем в столбец остатков (таблица 4.14).

Т а б л и ц а 4.14 – Обработанная таблица существенных переменных

Разрешенные наборы	Запрещенные наборы	Остатки

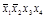
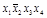
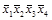
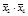
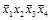
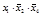
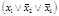
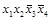
4-й этап. Строим таблицу покрытий существенных переменных (таблица 4.15), не забыв раскрыть скобки для тех остатков, где скобки имеются.

Т а б л и ц а 4.15 – Таблица покрытий существенных переменных

Остатки	Существенные переменные
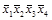
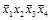
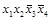
	Ú		Ú
	Ú	Ú	Ú	Ú
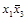
			Ú	Ú	Ú
				Ú	Ú

5-й этап. Обработаем таблицу покрытий. В качестве ядра минимальной функции выбираем конъюнкцию , так как она единолично перекрывает столбец 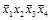. Из таблицы видно, что существует два варианта дополнений – конъюнкци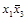и и . Первую конъюнкцию следует выбрать в качестве дополнения в том случае, если упрощенная функция будет реализовываться в базисе «ИЛИ-НЕ», а вторую – если упрощенная функция будет реализовываться в базисах «И-ИЛИ-НЕ» либо «И-НЕ». Такое применение дополнений позволит избежать лишних инверсий при реализации упрощенной функции.

Таким образом, упрощенный вариант функции, заданной таблицей 4.9, для базисов реализации «И-ИЛИ-НЕ» и «И-НЕ» имеет вид 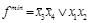, а для базиса «ИЛИ-НЕ» – . Кроме того необходимо помнить и о скобочных формах функций, которые позволяют сокращать количество используемых логических элементов. Так, функцию можно еще больше упростить, если вынести за скобки переменную . В результате получится функция .

Дата добавления: 2015-07-02