Решение. Теоретические вопросы

Пример 1.

ВЫПОЛНЕНИЯ ЗАДАНИЙ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ

Теоретические вопросы

ТЕМА 7. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

1. Перечислите основные задачи математической статистики.

2. Что такое статистическая гипотеза и какие вы знаете этапы её проверки?

3. Дайте понятие генеральная совокупности, выборки, статистики.

4. Какие точечные оценки вы знаете?

5. Выборочные оценки математического ожидания и дисперсии, выборочная оценка вероятности, выборочная оценка «доли», выборочная оценка линейного коэффициента корреляции Пирсона

5. В чем заключаются свойства несмещенности, состоятельности, эффективности точечных оценок?

6. Интервальные оценки. Построение доверительных интервалов для параметров. Приведите примеры (построение доверительного интервала для «доли»).

7. Что называется статистическим критерием?

8.Расшифруйте понятия: выборка, уровень значимости, критическая область гипотезы.

9. Приведите примеры (проверка гипотез о виде закона распределения, о параметрах закона распределения).

Дана выборка значений некоторого непрерывного распределенного количественного признака Х, объем выборки n = 50:

-2,25	0,38	-1,31	-1,05	-0,07	-4,17	3,69	-1,47	2,34	-1,22
0,42	-3,24	0,95	-0,68	0,15	1,75	0,71	-3,37	0,95	0,99
-3,1	-2,79	-1,15	2,26	0,21	1,37	-1,62	1,41	3,95	-1,05
-0,03	-2,49	-0,52	2,91	-5,71	0,91	-3,78	-0,14	-0,82	-2,4
3,78	1,17	-1,79	0,16	2,02	-3,88	0,64	-1,08	3,18	-0,84

Требуется:

1) Построить интервальный ряд, определив количество интервалов по формуле Стерджеса, рассчитать частоты, относительные частоты (частости), накопленные частоты, накопленные частости.

2) Построить гистограмму, кумуляту.

3) Найти средние величины: выборочное среднее, медиану, моду.

4) Найти показатели вариации: размах, среднее линейное отклонение, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение, коэффициент вариации.

1) Построим интервальный ряд: .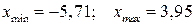

Согласно формуле Стерджеса рекомендуемое число интервалов:

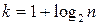
Т.к. n =50, то 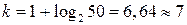. Начало первого интервала 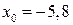Конец последнего, седьмого интервала (минимальное и максимальное значение признака округлили в соответствующую сторону с точностью до десятых: для нижней границы – до десятых вниз, для верхней границы – до десятых вверх).

Длина каждого интервала будет равна .

Подсчитаем число вариант, попадающих в каждый интервал, получим вариационный ряд:

	[-5.8; -4.4)	[-4.4; -3)	[-3; -1.6)	[-1.6; -0.2)	[-0.2; 1.2)	[1.2; 2.6)	[2.6; 4)

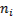
Разделив частоты на объем выборки найдем относительные частоты (частости): 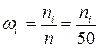и запишем вариационный ряд с частостями и накопленными частотами и частостями (накопленные частоты подсчитывали как количество вариант, значения которых меньше правой границы каждого интервала).

Получаем:

	[-5.8; -4.4)	[-4.4; -3)	[-3; -1.6)	[-1.6; -0.2)	[-0.2; 1.2)	[1.2; 2.6)	[2.6; 4)
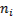
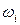
	0,02	0,12	0,12	0,22	0,3	0,12	0,1
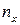
	0,02	0,14	0,26	0,48	0,78	0,9

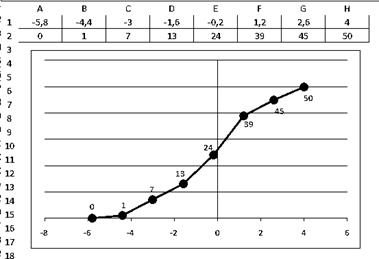
2) Построим гистограмму частот в MS Excel:

Построим кумуляту для интервального ряда – ломанную, которая начинается с точки, абсцисса которой равна началу первого интервала, а ордината – нулю; другие точки этой ломанной соответствуют концам интервалов и накопленным частотам. Воспользуемся средствами MS Excel:

3) Найдем средние величины.

Среднее выборочное:

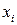, где - середины интервалов.

Найдем медиану интервального ряда – значение признака, приходящегося на середину ранжированного ряда наблюдений. Сначала определяем интервал медианы – первый интервал, в котором накопленная частота окажется больше половины объема выборки, т.е. больше 25.

Таким интервалом в нашем случае является [-0,2; 1,2].

Найдем моду интервального ряда – значение признака, которому соответствует наибольшая частота. Сначала определяем интервал моды – интервал с наибольшей частотой: [-0.2; 1.2].

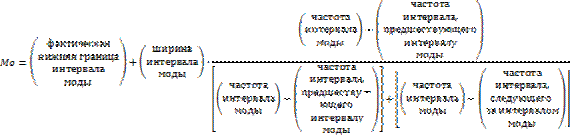
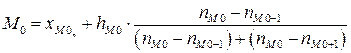
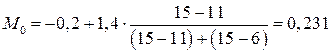
4) Найдем показатели вариации.

Размах: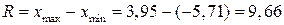

Среднее линейное отклонение:

, где - середины интервалов,

Выборочная дисперсия:

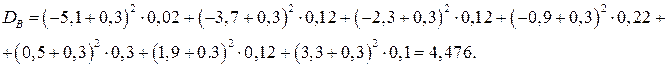
Выборочное среднее квадратическое отклонение:

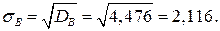
Коэффициент вариации:

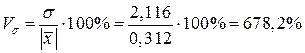
Рассчитанная величина свидетельствует о неоднородности совокупности, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному). Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

Исправленные выборочная дисперсия и среднее квадратическое отклонение:

Пример 2. Имеются выборочные данные социологических опросов о динамике предвыборных рейтингов некоторой политической партии (в процентах) в выбранном регионе страны за предыдущие 10 недель:

А

Найти доверительные интервалы для выборочных оценок «истинных» рейтингов данной политической партии в указанном регионе (среднего значения 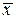, дисперсии 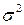и стандартного отклонения 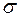генеральной совокупности) при доверительной вероятности .

Решение. Составим ряд распределения и найдем среднее значение 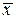, дисперсию и стандартное отклонение S.

xi
ni

;

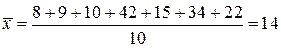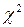Из таблицы распределения Стьюдента найдем , а из таблицы - распределения пару и 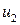, такую что 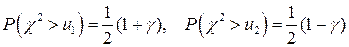, т. е , .

,

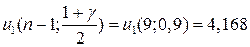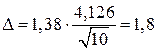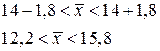- доверительный интервал для среднего значения.

Доверительный интервал для дисперсии:

;

.

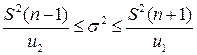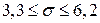Дата добавления: 2015-07-02