Решение. 1 страница

Пример 3. Исходные данные

По 10 странам Западной Европы имеются следующие данные:

Х – доля расходов домашних хозяйств на конечное потребление, % к ВВП;

У – индекс развития человеческого потенциала, %.

Признаки Х и У имеют нормальный закон распределения.

Х
У	0,71	0,80	0,95	0,77	0,95	0,89	0,99	0,80	0,86	0,95

1. Рассчитайте оценки a, b параметров уравнения парной линейной регрессии.

2. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции (α = 0,05).

4. Рассчитайте выборочный коэффициент детерминации. Сделайте вывод.

1. Рассчитаем оценки параметров линейной модели методом наименьших квадратов

y = a + bx

№	хi	уi	хi^2	хi уi	уi^2	ŷi	(уi - ŷi)^2	(ус - ŷi)^2	(уi - ус)^2	(хi – хс)^2
		0,71		40,47	0,5041	0,728	0,000324	0,01932	0,025	243,36
		0,80		53,6	0,64	0,817	0,000289	0,0025	0,004	31,36
		0,95		74,1	0,9025	0,9151	0,00122	0,0023	0,007	29,16
		0,77		49,28	0,5929	0,79	0,0004	0,00593	0,009	73,96
		0,95		78,85	0,9025	0,96	0,0001	0,00865	0,007	108,16
		0,89		66,75	0,7921	0,888	0,000004	0,00044	0,001	5,76
		0,99		87,12	0,9801	1,00	0,0001	0,01769	0,015	237,16
		0,80		48,8	0,64	0,763	0,00137	0,01082	0,004	134,56
		0,86		61,06	0,7396	0,852	0,000064	0,00023	0,00	2,56
		0,95		77,9	0,9025	0,949	0,000001	0,00672	0,007	88,36
∑		8,67		637,93	7,5963	8,66	0,0039	0,0746	0,079	954,4

Найдем оценки a и b, используя систему уравнений для линейной зависимости.

Система нормальных уравнений:

;

.

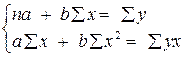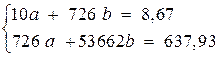Решая систему, получим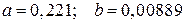

Линейная модель имеет вид: ŷ = 0, 221 + 0,00889х

2. Оценим тесноту взаимосвязи между признаками с помощью линейного коэффициента корреляции:

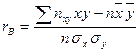
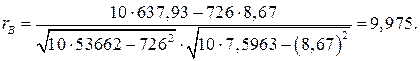
Коэффициент показывает высокую тесноту связи (прямолинейная зависимость).

Проверим значимость выборочного коэффициента корреляции.

Выдвигаем нулевую гипотезу (Н₀) об отсутствии линейной зависимости.

Конкурирующая гипотеза (Н₁) определяет двустороннюю критическую область.

Распределение Стьюдента с k = n – 2 = 10 – 2 = 8.

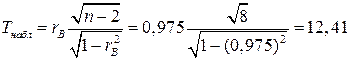
T_табл (0,05; 8) = 2,31.

Так как, 12,41 > 2,31, то отклоняем гипотезу об отсутствии линейной зависимости. Другими словами, коэффициент корреляции статистически значим.

Коэффициент показывает высокую тесноту связи - прямолинейная зависимость между долей расходов домашних хозяйств на конечное потребление и индексом развития человеческого потенциала, что подтверждается экономической теорией.

4. Рассчитаем выборочный коэффициент детерминации. Для этого возведем коэффициент корреляции в квадрат.

R_в² = (r_в)² = 0,975² = 0,951

Коэффициент детерминации характеризует долю вариации признака У (индекс развития человеческого потенциала), объясненную линейным уравнением регрессии.

Таким образом, в среднем 95,1% вариации индекса развития человеческого потенциала объясняется вариацией доли расходов домашних хозяйств на конечное потребление в ВВП, а 4,9% зависит от вариации неучтенных в модели факторов.

Пример 4. Приведем необходимые формулы.

Выборочное уравнение прямой линии регрессии Y на X имеет вид

,

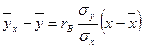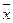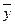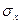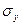где и – выборочные средние признаков X и Y, и – выборочные средние квадратические отклонения, 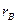– выборочный коэффициент корреляции:

.

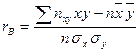Если данные наблюдений над признаками X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам

, ,

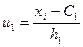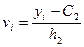где C₁ – ложный нуль вариант X, h₁ – шаг, т.е. разность между двумя соседними вариантами; С₂ – ложный нуль вариант Y, h₂ – шаг вариант Y. В этом случае выборочный коэффициент корреляции имеет вид:

.

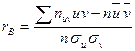Величины 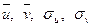могут быть найдены либо методом произведений (при большом числе данных), либо непосредственно по формулам:

, , , .

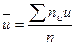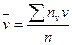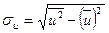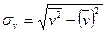Тогда величины, входящие в уравнение регрессии, можно пересчитать по формулам:

, , , .

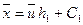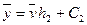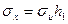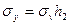Решение. Найти выборочное уравнение прямой линии регрессии Y на X по данным, приведенным в корреляционной таблице:

y x
			–	–	–
	–			–	–
	–	–
	–	–
	–	–	–
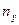
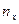
						n=100

Составим корреляционную таблицу в условных вариантах, выбрав в качестве ложных нулей С₁ = 30, С₂ = 36, так как 32 – максимальная частота, встречающаяся в таблице.:

v u	-2	-1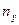
-2			–	–	–
-1	–			–	–
	–	–
	–	–
	–	–	–
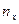
						n=100

Найдем 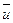и :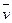

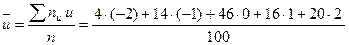= 0,34;

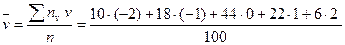=– 0,04.

Найдем 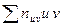, для чего составим расчетную таблицу:

u v	-2	-1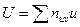
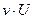
-2	-8 -8	-6 -12	–	–	–	-14
-1	–	-8 -8	-10	–	–	-8
	–	–
	–	–
	–	–	–
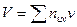
	-8	-20	-6			–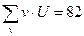

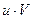
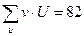
Найдем вспомогательные величины 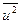и :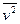

;

.

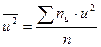
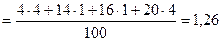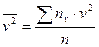
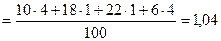Найдем :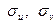

= ;

.

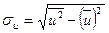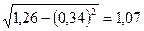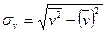
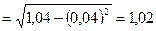Найдем искомый выборочный коэффициент корреляции:

= .

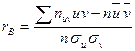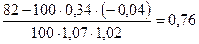Найдем шаги

h₁ = 25 – 20 = 5; h₂ = 26 – 16 = 10.

Найдем 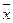и :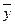

;

.

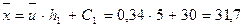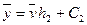
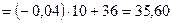Найдем 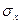и :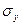

= ;

= .

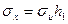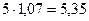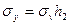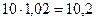Искомое уравнение прямой линии регрессии Y на X:

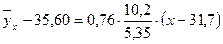
или окончательно

.

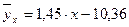Коэффициент детерминации для линейной регрессии равен квадрату коэффициента корреляции: 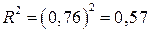. Коэффициент детерминации характеризует долю вариации признака y, объясненную линейным уравнением регрессии. Таким образом, в среднем 57,76 % случаев изменения х приводят к изменению y, а 42,24% зависит от вариации неучтенных в модели факторов.

Значимость коэффициента корреляции

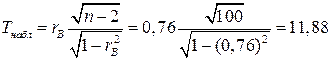
По таблице критических точек распределения Стьюдента находим T_табл при k=n-2

T_табл (k; 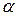) = (98;0.1) = 1,66

Поскольку T_набл > T_табл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически значим. Интервальная оценка для коэффициента корреляции (доверительный интервал)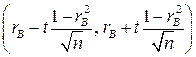

Доверительный интервал для коэффициента корреляции .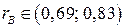

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Задача 1. Дана выборка значений некоторого непрерывного количественного признака Х, объем выборки n=50.

Требуется:

1) Построить интервальный ряд, определив количество интервалов по формуле Стерджеса, рассчитать частоты, относительные частоты (частости), накопленные частоты, накопленные частости.

2) Построить гистограмму, кумуляту.

3) Найти средние величины: выборочное среднее, медиану, моду.

4) Найти показатели вариации: размах, среднее линейное отклонение, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение, коэффициент вариации.

Вар 1	Вар 2	Вар 3	Вар 4	Вар 5	Вар 6	Вар 7	Вар 8	Вар 9	Вар 10
3,92	2,84	-1,09	4,38	1,76	10,53	5,65	9,72	6,08	12,47
3,32	0,69	2,81	1,52	1,68	1,77	6,81	11,68	7,02	12,13
-0,22	2,72	5,66	7,06	7,66	8,36	11,91	7,57	12,82	13,52
1,70	0,54	3,56	3,70	7,49	7,18	4,42	6,28	7,73	13,74
1,37	6,54	4,78	4,69	4,63	6,20	7,50	6,41	11,11	10,12
-1,19	1,06	2,76	3,43	4,06	6,75	6,68	7,50	7,95	14,09
0,54	1,77	4,43	2,63	6,51	5,59	3,56	8,91	12,89	8,09
4,56	1,49	4,31	3,62	5,92	2,35	10,46	5,69	8,47	10,90
3,41	3,69	4,60	5,71	5,89	4,55	5,49	5,43	11,08	8,27
2,50	2,05	-0,26	6,66	5,18	5,77	5,71	7,08	9,73	8,79
0,61	0,83	3,00	3,66	1,51	10,96	7,15	7,28	8,18	9,68
-0,92	4,43	3,76	2,06	6,85	4,92	6,81	5,98	11,63	8,92
0,74	-3,05	3,45	1,33	4,04	6,37	6,05	7,75	6,44	10,10
2,47	0,60	3,15	3,08	5,73	8,39	7,73	9,84	10,37	9,56
2,08	6,43	1,15	7,80	6,60	9,10	11,38	8,35	11,16	10,54
1,41	0,58	-1,15	3,52	7,23	0,75	7,05	7,40	8,96	7,86
-0,28	6,20	-0,99	2,62	7,43	1,73	5,51	7,03	10,58	9,98
2,01	4,13	1,79	7,37	2,65	4,07	9,28	6,72	10,07	7,73
0,02	2,55	4,14	4,94	7,09	4,57	2,91	5,89	12,53	12,47
-0,60	3,02	2,39	5,74	8,19	7,14	6,37	11,49	8,74	12,76
-0,23	2,12	1,17	3,55	5,37	9,23	5,85	8,96	10,73	10,19
-0,24	4,99	3,27	3,71	2,94	6,27	2,99	9,66	13,11	8,05
3,96	-1,67	1,21	6,76	9,25	5,67	8,59	9,42	6,56	10,35
4,24	0,30	2,19	9,13	4,56	5,36	11,27	11,54	6,22	11,16
0,62	1,70	1,76	1,99	8,41	4,67	4,47	8,27	9,53	6,07
-0,17	2,48	0,75	2,94	5,02	7,01	7,42	6,90	9,72	11,59
2,30	3,14	3,78	-0,03	6,75	3,89	5,50	9,61	8,89	7,71
-1,26	1,62	1,25	5,85	2,51	9,38	8,39	10,63	8,25	11,37
1,43	-0,37	2,87	5,41	7,45	2,89	4,81	11,79	8,48	12,28
-2,44	5,94	4,74	4,80	1,91	6,28	7,08	6,93	7,62	8,26
1,83	4,51	0,54	2,21	7,18	8,60	3,33	11,83	7,78	10,68
3,88	0,47	1,41	3,68	4,35	2,15	6,41	10,14	8,93	9,03
6,06	3,63	3,53	2,07	-0,40	6,78	7,14	7,21	8,86	8,02
-2,27	2,01	3,66	-0,29	4,53	7,79	5,80	6,70	9,43	11,40
-3,20	1,40	3,17	3,27	4,80	6,74	8,14	7,68	9,83	10,69
0,59	1,48	3,92	1,73	5,25	5,63	5,56	8,13	10,91	8,72
1,88	4,04	4,73	4,25	7,64	3,33	11,08	9,68	10,04	9,19
4,62	-0,12	5,08	2,55	4,29	3,20	8,78	8,53	10,42	10,10
-0,63	1,63	3,41	3,50	6,21	6,57	7,98	5,07	9,93	9,07
2,70	0,48	4,95	4,19	1,41	6,86	8,17	6,62	10,51	10,58
0,69	4,41	0,78	5,84	5,46	6,48	8,62	9,84	12,01	7,21
1,57	0,91	2,24	4,28	7,25	8,80	4,75	10,11	9,64	11,71
0,06	3,09	6,96	1,44	5,13	9,49	8,54	9,75	4,97	8,80
1,41	2,50	5,66	2,48	5,59	4,75	6,46	6,70	13,37	9,71
3,93	4,58	1,66	0,96	2,34	4,23	8,04	4,93	8,71	8,52
-1,17	1,62	3,79	8,06	3,17	2,11	6,29	7,61	6,70	9,48
0,00	5,89	0,50	2,48	5,44	7,84	4,10	9,94	6,85	10,38
-0,56	0,68	2,57	1,65	3,24	6,73	3,59	6,40	10,25	10,88
-0,09	0,78	-0,04	2,69	7,67	6,73	7,97	7,89	4,43	3,92
5,10	0,29	1,08	5,10	5,87	5,96	10,40	6,77	9,36	8,19
Вар 11	Вар 12	Вар 13	Вар 14	Вар 15	Вар	Вар 17	Вар 18	Вар 19	Вар 20
10,17	10,23	13,49	12,25	14,04	1,35	3,73	4,89	4,44	6,49
9,95	12,25	12,01	14,41	19,12	-2,43	3,37	-0,41	3,01	7,61
9,22	12,10	13,62	12,13	14,04	4,61	5,10	1,89	9,32	12,68
10,40	10,40	14,12	13,34	14,93	2,08	2,25	5,45	4,59	8,85
9,70	12,22	14,35	14,21	14,70	-1,45	0,69	3,75	5,01	-1,15
11,76	9,89	9,90	12,27	15,94	2,91	1,95	6,59	-0,98	10,10
12,16	12,24	11,94	16,92	15,64	3,28	2,11	1,02	5,60	3,86
10,45	10,48	11,66	14,52	14,30	-0,67	5,69	7,99	4,68	7,46
10,31	12,24	12,28	14,47	13,56	3,73	-2,86	2,79	1,40	3,90
6,96	8,39	14,14	11,81	14,75	2,36	0,95	2,75	5,19	1,77
9,05	9,93	12,09	15,68	15,19	-0,50	2,43	-0,18	6,37	4,66
10,28	13,01	14,91	16,86	17,99	2,46	2,38	4,05	3,02	7,31
11,24	8,67	14,35	15,02	16,40	1,46	1,87	3,39	4,77	6,76
9,52	12,49	15,51	8,29	16,67	4,42	2,29	0,82	5,15	4,99
9,41	14,66	13,54	14,35	18,76	3,08	2,32	3,83	5,44	7,59
10,19	10,38	16,04	15,99	15,35	-0,77	0,78	3,97	3,26	1,52
12,23	13,52	12,07	12,99	18,45	3,79	-3,26	2,34	1,46	4,78
12,13	12,83	11,68	18,42	12,66	0,90	2,40	0,70	1,33	10,70
10,46	13,35	10,10	13,79	14,87	-1,72	-5,55	4,85	7,93	-0,93
12,16	10,55	13,48	15,35	17,55	3,37	3,86	3,64	6,22	1,74
10,53	9,25	10,12	14,16	15,75	-1,83	2,83	5,83	3,25	6,38
11,48	11,66	10,11	13,37	14,69	-2,53	1,13	1,74	3,65	7,67
7,60	13,63	13,21	12,95	12,98	0,00	2,81	4,17	-0,25	4,68
13,23	13,14	15,48	14,38	15,65	1,62	1,83	-4,04	4,06	9,87
12,31	13,49	13,76	16,09	12,59	4,13	-0,36	-2,37	7,02	10,46
14,87	9,59	11,75	13,96	12,84	0,58	2,59	-0,35	7,34	6,38
11,15	9,57	12,00	13,15	15,19	1,71	1,03	1,96	4,01	-0,01
9,10	14,29	12,06	13,94	15,53	0,71	-4,42	2,79	4,72	5,21
11,91	11,02	15,64	14,34	12,11	-2,70	1,82	0,15	3,82	4,95
9,89	11,31	14,16	13,95	16,73	-0,20	9,44	0,46	3,25	3,60
10,03	16,39	14,41	13,64	13,57	3,73	-2,43	4,20	2,17	3,68
10,50	12,61	10,24	13,43	14,48	-1,57	1,97	2,43	1,28	3,74
13,44	10,61	13,65	18,03	11,94	-2,40	-1,37	7,59	-1,82	2,50
15,33	10,74	12,33	17,04	15,55	-1,04	0,87	4,71	6,91	4,78
8,17	12,62	14,41	18,11	17,44	-0,47	-0,44	3,67	5,30	11,10
16,94	11,94	9,87	12,96	12,96	3,67	5,21	2,00	-0,72	3,36
8,49	16,81	11,99	16,07	19,11	4,03	1,44	0,99	5,78	-1,65
9,80	15,07	15,84	14,22	14,12	3,69	-0,39	0,23	1,43	8,23
11,15	14,72	10,68	13,05	13,38	-1,25	3,97	2,63	9,13	7,73
9,84	11,94	12,99	13,07	11,43	6,86	5,38	4,16	7,66	4,06
11,35	15,18	13,52	12,13	17,60	0,38	3,01	8,62	5,58	1,44
10,02	11,94	13,66	9,11	15,18	1,87	2,22	5,90	1,31	10,86
7,54	10,71	15,90	16,01	15,54	-1,83	9,21	3,37	1,86	6,42
8,67	13,59	11,34	12,87	10,61	0,05	2,21	4,39	2,14	6,33
8,95	7,62	12,89	15,55	17,05	2,33	1,82	1,97	9,97	-1,18
11,04	11,56	18,01	12,99	17,84	6,65	1,94	6,39	7,14	5,48
12,80	15,52	16,96	15,23	13,65	-0,36	4,22	5,40	4,27	0,09
8,66	12,69	11,87	15,92	13,85	1,49	3,69	5,88	0,15	0,76
14,67	12,05	13,20	15,70	15,60	-1,14	4,27	3,15	3,42	4,91
9,98	9,72	15,28	13,58	14,45	1,87	4,03	6,49	2,64	4,26
Вар 21	Вар 22	Вар 23	Вар 24	Вар 25	Вар 26	Вар 27	Вар 28	Вар 29	Вар 30
2,88	3,09	2,12	15,30	5,95	13,01	12,75	14,08	16,80	14,73
6,83	7,28	5,59	12,76	6,12	13,26	11,23	11,02	15,16	13,65
9,24	6,55	9,74	10,70	10,13	10,65	12,06	16,74	16,34	15,72
1,74	4,89	13,34	6,32	10,78	11,90	10,38	9,14	13,48	11,29
5,45	4,77	8,21	10,29	12,07	11,71	9,16	16,93	11,91	14,63
2,68	9,77	9,13	15,66	8,02	11,20	12,58	11,84	12,99	17,16
11,05	8,76	6,03	12,94	13,00	14,07	12,10	13,34	12,43	13,55
6,46	6,57	10,53	9,09	9,82	15,58	16,73	13,20	10,16	11,74
5,09	3,55	9,90	5,03	14,58	13,51	10,93	16,97	17,10	19,09
11,82	8,75	9,24	6,28	8,34	10,67	9,76	10,37	16,82	13,69
6,84	13,08	11,43	11,85	4,50	9,82	7,20	11,94	15,68	18,74
3,84	8,45	5,75	8,41	13,45	13,42	11,36	12,23	15,16	11,66
9,84	9,27	10,94	10,68	7,32	10,90	16,66	11,29	13,39	8,96
4,85	6,17	8,42	5,52	6,13	12,56	13,18	10,38	15,93	18,67
12,52	10,03	8,64	4,65	8,06	11,22	15,05	13,95	11,94	11,49
7,36	4,67	12,80	5,09	8,27	5,39	9,48	15,70	16,16	11,20
7,19	6,89	-0,06	9,98	10,88	14,53	7,21	12,33	12,25	11,12
6,70	4,88	7,68	4,37	6,98	13,13	7,70	14,48	13,94	18,64
6,62	8,07	8,51	10,48	6,90	14,08	13,76	12,59	11,19	18,90
5,32	13,40	6,09	8,81	6,11	14,00	14,22	13,55	17,61	10,29
5,32	4,68	6,39	7,13	10,99	9,21	15,06	4,44	16,89	14,39
8,66	7,09	10,02	8,87	14,73	12,71	16,04	15,10	11,29	10,62
4,68	8,56	7,81	8,54	11,52	12,64	11,66	12,58	16,19	17,20
4,70	5,11	6,26	5,28	10,85	12,25	10,12	15,23	19,56	15,96
11,49	9,14	9,61	13,92	6,47	14,74	5,98	12,12	13,40	21,74
7,70	6,63	3,52	0,60	16,41	13,24	8,81	6,45	15,23	13,46
4,48	0,87	4,21	6,83	7,49	9,85	9,86	12,82	12,93	9,41
2,89	5,92	2,49	8,88	11,57	12,13	9,17	10,90	17,77	16,27
9,56	9,91	7,04	3,54	10,13	7,64	11,57	11,91	11,53	13,38
0,99	7,37	9,86	9,53	8,61	12,24	13,84	14,30	14,10	14,18
5,98	8,24	9,48	10,15	4,93	9,83	8,24	13,69	13,62	19,08
7,73	1,47	9,65	5,48	8,02	9,57	9,14	11,53	17,06	10,06
7,09	10,15	8,42	11,30	10,87	8,85	9,64	7,59	11,33	15,79
7,85	10,90	3,29	9,10	11,34	12,63	11,40	13,90	15,04	13,95
6,22	9,11	8,92	13,12	8,40	16,88	8,04	16,24	11,35	14,09
5,90	2,04	9,03	6,30	13,79	11,36	14,37	17,33	13,13	13,14
5,30	6,78	6,23	9,56	10,42	16,23	10,86	13,60	9,15	17,57
3,59	4,86	7,42	8,59	5,64	5,64	16,05	16,52	12,43	9,74
7,99	7,95	11,17	7,55	14,33	9,06	11,31	10,95	11,90	7,27
9,50	7,40	5,04	14,05	17,09	11,53	5,42	14,42	14,55	20,80
0,78	7,34	6,54	10,75	14,22	8,28	12,11	10,81	21,39	13,71
0,90	7,73	8,12	9,60	8,21	13,31	13,89	9,21	12,85	14,07
6,54	9,18	10,61	8,00	11,80	16,49	11,09	10,01	12,87	15,75
9,13	7,68	4,51	12,34	10,01	7,45	12,63	15,47	17,16	12,33
6,10	8,71	7,60	8,12	8,21	6,98	15,61	13,46	10,71	12,87
4,17	4,98	9,20	8,81	11,49	12,63	14,47	12,86	13,99	14,47
6,16	5,40	-1,16	10,91	10,87	9,61	11,96	16,06	14,51	19,73
5,61	7,25	16,75	8,72	11,72	10,28	18,13	13,11	8,15	13,11
5,20	4,74	8,60	12,96	6,67	14,58	13,34	11,44	16,31	18,40
6,61	10,21	8,81	10,88	6,92	8,41	16,56	15,85	12,29	13,96

Дата добавления: 2015-07-02