Решение. Функцию распределения находим по формуле

Функцию распределения находим по формуле .

Математическое ожидание вычислим по формуле:

.

Для нахождения дисперсии воспользуемся формулами:

.

Дисперсия случайной величины:

,

откуда легко определить среднеквадратическое отклонение:

.

Моду найдём по максимальной вероятности .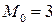

Пример 10. Задана плотность распределения вероятностей непрерывной случайной величины . Требуется:

1). Определить коэффициент ;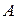

2). Найти функцию распределения ;

3). Найти математическое ожидание и дисперсию ;

4).Найти вероятность того, что примет значение из интервала .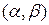

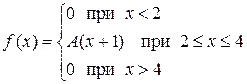
Решение. 1). Для определения коэффициента 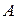воспользуемся свойством нормированности плотности распределения:

,

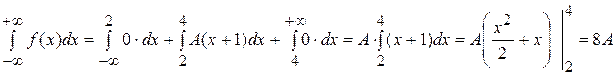т.е. 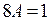, отсюда . Таким образом,

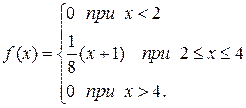
2). Для нахождения функции распределения используем формулу

При 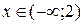, имеем: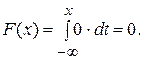

При ,

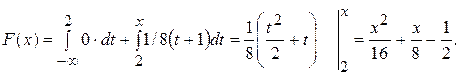
Если ,

Таким образом,

3). Найдем математическое ожидание и дисперсию :

Теперь найдём дисперсию:

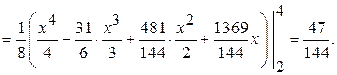
4). Вероятность того, что примет значение из интервала :

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

а) Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта (V – номер варианта);

б) Определить испытания и элементарные события;

в) Определить исследуемое событие А и другие события;

г) Установить, какие формулы следует использовать и выполнить вычисления.

1. Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность, что буквы вынимаются в порядке заданного слова, в качестве заданного слова используется ваша фамилия.

2. В урне содержится К черных и Н белых шаров. Случайным образом вынимают М шаров. Найти вероятность того, что среди них имеется:

а) Р белых шаров;

б) меньше, чем Р белых шаров;

в) хотя бы один белый шар.

Вариант

К

Н

М

Р

Вариант

К

Н

М

Р

3. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями р₁, р₂, и р₃. Найти вероятность того, что за время Т выйдет из строя:

а) только один элемент;

б) хотя бы один элемент.

Значения параметров вычислить по следующим формулам:

.

4. Вероятность того, что новый товар фирмы будет «пользоваться спросом» на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна р₁. Вероятность того, что товар будет «пользоваться спросом» при наличии на рынке конкурирующего товара равна р₂. Вероятность появления на рынке конкурирующего товара равна . Найдите вероятность того, что новый товар фирмы будет «пользоваться спросом» на рынке.

Значения параметров вычислить по следующим формулам:

.

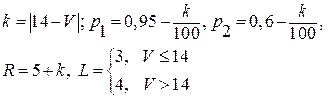5. В магазин поступают партии товаров трех заводов-изготовителей в количестве М₁, М₂, М₃ штук. Вероятности того, что в соответствующей партии товаров нет бракованных изделий соответственно равны р₁, р₂, и р₃. Покупатель выбирает товар случайным образом. Найти вероятность того, что купленный товар хорошего качества был поставлен соответственно первым, вторым или третьим заводом. Значения параметров вычислить по следующим формулам:

.

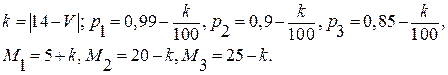6. В каждом из n независимых испытаний событие А происходит с постоянной вероятностью p. Вычислить все вероятности 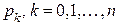, где k – частота события А. Построить график найти наивероятнейшую частоту. Значения параметров n и p вычислить по формулам:

.

7. В каждом из n независимых испытаний событие А происходит с постоянной вероятностью p. Найти вероятность того, что событие происходит:

а) точно М раз;

б) меньше чем М и больше чем L раз;

в) больше чем М раз.

Значения параметров n, М, L и p вычислить по формулам:

.

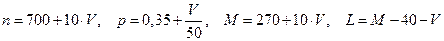8. На телефонной станции неправильное соединение происходит с вероятностью р. Найти вероятность того, что среди n соединений:

а) точно G неправильных соединений;

б) меньше чем L неправильных соединений;

в) больше чем М неправильных соединений.

Значения параметров p, n, М, L и G вычислить по формулам:

.

9. Случайная величина X задана рядом распределения.

X
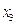
p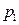

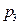
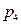
Найти функцию распределения случайной величины, построить ее график. Вычислить для X математическое ожидание, дисперсию и моду. Значения параметров вычислить по формулам:

.

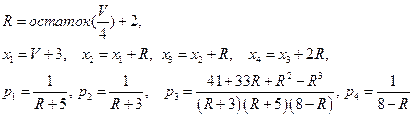10. Случайная величина X задана функцией распределения

Найти коэффициент , функцию распределения F(x) случайной величины, её математическое ожидание, дисперсию и вероятность попадания в интервал 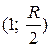. Построить графики функций f(x) и F(x). Значения параметров K и R вычислить по формулам K=2+V, R=2K.

Дата добавления: 2015-07-02