
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выполнения заданий. Теоретические вопросы
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ
Теоретические вопросы
ТЕМА 5. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
1. Сформулируйте постановку следующих экономико-математических моделей: задача о ресурсах, задача и диете, транспортная задача.
2. Запишите стандартную форму записи задачи линейного программирования.
3. Приведите алгоритм графического метода решения задач линейного программирования, для какого вида задач он применим?
4. Какие переменные называются базисными в задаче линейного программирования?
6. Что такое допустимое и оптимальное решение задачи линейного программирования?
7. Сформулируйте основную идею симплекс-метода.
8. Сформулируйте признак неограниченности решения в симплекс-методе.
9. Как составить опорный план транспортной задачи?
10. Сформулируйте экономический смысл целевой функции, ограничений и переменных транспортной задачи.
Пример 1.. Пусть бригада имеет: 300 кг металла, 100 м2 стекла, 160 чел. / час. рабочего времени. Надо изготовить: изделия А и В. Прибыль от реализации изделий: А — 10 у.е., В — 12 у.е. Для изготовления изделия А расходуется: 4 кг металла, 2 м2 стекла и 2 чел./час. рабочего времени. Для изготовления изделия В расходуется: 5 кг металла, 1 м2 стекла и 3 чел./час. рабочего времени. Требуется спланировать выпуск продукции так, чтобы прибыль была максимальной. Решить задачу симплекс-методом.
Решение. Математическая постановка задачи.
Пусть 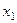 и
и 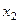 — количество изделий А и В, тогда ресурсы сырья и рабочего времени запишем в виде ограничений—неравенств:
— количество изделий А и В, тогда ресурсы сырья и рабочего времени запишем в виде ограничений—неравенств:
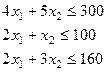
Прибыль от реализации всей продукции составит

Это типичная задача линейного программирования (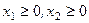 ). Вид данной задачи не канонический, поскольку условия имеют вид неравенств, а не уравнений. Сведем ее к каноническому виду, добавив дополнительные переменные
). Вид данной задачи не канонический, поскольку условия имеют вид неравенств, а не уравнений. Сведем ее к каноническому виду, добавив дополнительные переменные 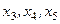 по числу ограничений - неравенств:
по числу ограничений - неравенств:
 (1)
(1)
При этом 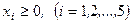 . Выделение новых переменных не влияет на вид целевой функции. Они будут указывать на остатки ресурсов, не использованные в производстве.
. Выделение новых переменных не влияет на вид целевой функции. Они будут указывать на остатки ресурсов, не использованные в производстве.
Перепишем систему (1) в более удобном виде, выразив дополнительные переменные
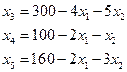 (2)
(2)
Чтобы свести данную задачу к задаче минимизации целевой функции, функцию 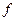 нужно взять со знаком минус:
нужно взять со знаком минус:
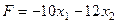
Запишем условие задачи в виде таблицы
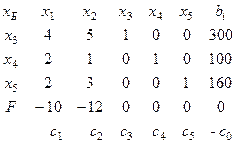 (3)
(3)
Так как все 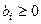 , то в качестве начального опорного решения можно взять следующее решение:
, то в качестве начального опорного решения можно взять следующее решение:
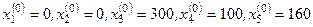
Этому решению соответствует значение целевой функции
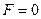
Оно не оптимально, так как эта величина может быть уменьшена за счет свободных параметров (коэффициенты 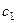 и
и 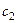 при неизвестных
при неизвестных 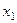 и
и 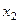 в целевой функции отрицательны). Наибольшим среди всех отрицательных
в целевой функции отрицательны). Наибольшим среди всех отрицательных 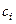 является коэффициент
является коэффициент 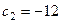 , которому соответствует переменная
, которому соответствует переменная 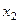 . Определим базисную переменную, которая первой станет равной 0 при увеличении значения
. Определим базисную переменную, которая первой станет равной 0 при увеличении значения 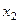 . Для этого вычислим следующие величины:
. Для этого вычислим следующие величины:

Наименьшей является величина 53,3, которая соответствует переменной  . Определим новое опорное решение из системы (2):
. Определим новое опорное решение из системы (2):
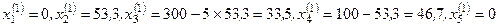
Значение целевой функции
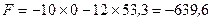
Это решение уже лучше.
Следующий шаг начнем с выбора нового базиса. Примем переменные 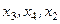 в качестве базисных и перейдем к этому базису. Результаты представлены в следующей таблице:
в качестве базисных и перейдем к этому базису. Результаты представлены в следующей таблице:
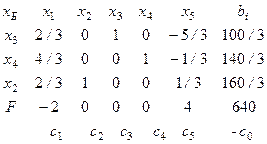 (4)
(4)
Этому решению соответствует значение целевой функции
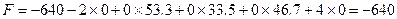
Оно не оптимально, так как эта величина может быть уменьшена за счет свободного параметра 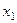 (коэффициент
(коэффициент 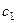 при неизвестном
при неизвестном 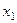 в целевой функции отрицателен). Определим базисную переменную, которая первой станет равной 0 при увеличении значения
в целевой функции отрицателен). Определим базисную переменную, которая первой станет равной 0 при увеличении значения 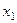 . Для этого вычислим следующие величины:
. Для этого вычислим следующие величины:
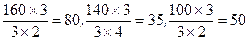
Наименьшей является величина 35, которая соответствует переменной 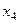 . Определим новое опорное решение:
. Определим новое опорное решение:
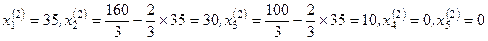
Значение целевой функции
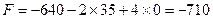
Это решение еще лучше предыдущего.
Следующий шаг начнем с выбора нового базиса. Примем переменные  в качестве базисных и перейдем к этому базису. Результаты представлены в следующей таблице:
в качестве базисных и перейдем к этому базису. Результаты представлены в следующей таблице:
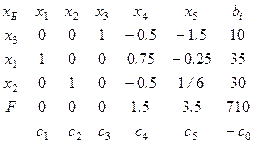 (5)
(5)
Коэффициенты при свободных неизвестных в целевой функции положительны, поэтому, при их увеличении целевая функция может лишь увеличиваться. Следовательно, решение, полученное на предыдущем шаге, является оптимальным, а значение целевой функции равно
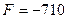
Ответ: Для получение максимума прибыли в 710 у.е. необходимо изготовить 35 изделий А и 30 изделий В. При этом все ресурсы стекла и рабочего времени будут использованы полностью, а металла останется 10 кг.
Пример 2. Найти опорное решение задачи методом северо-западного угла.
На три базы А1, А2, А3 поступил однородный груз в количествах, приведенных в таблице 3. Требуется перевезти этот груз в пять пунктов назначения В1, В2, B3, В4, В5, данные приведены в таблице 1. Составить опорный план методом северо-западного угла, и найти такой план закрепления потребителей и поставщиков, чтобы общие затраты на перевозки были минимальны (метод потенциалов).
Таблица 1
| Пункт отправления | Пункты назначения | Запасы | ||||
| 
| 
| 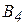
| 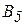
| ||
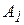
| ||||||

| ||||||
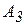
| ||||||
| Потребности |
Стоимость перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения известны. Найти план перевозок методом северо-западного угла.
Решение. Здесь число пунктов отправления m=3, а число пунктов назначения n=5. Заполнение таблицы начинаем с верхней левой клетки (1,1), т.е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Так как запасы пункта А1 больше, чем потребности пункта В1, то полагаем 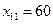 , записываем это значение в клетке (1,1) и временно исключаем из рассмотрения столбец В1, считая при этом запасы А1=80. Рассматриваем далее первые из оставшихся пунктов отправления А1 и назначения В2. Запасы пункта А1 больше потребностей пункта В2. Положим
, записываем это значение в клетке (1,1) и временно исключаем из рассмотрения столбец В1, считая при этом запасы А1=80. Рассматриваем далее первые из оставшихся пунктов отправления А1 и назначения В2. Запасы пункта А1 больше потребностей пункта В2. Положим 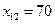 , запишем это значение в клетку (1,2) и временно исключим из рассмотрения столбец В2. В пункте А1 осталось 10 единиц груза. Снова рассмотрим первые из оставшихся пунктов отправления А1 и пунктов назначения В3. Потребности В3 больше оставшихся запасов пункта А1. Положим
, запишем это значение в клетку (1,2) и временно исключим из рассмотрения столбец В2. В пункте А1 осталось 10 единиц груза. Снова рассмотрим первые из оставшихся пунктов отправления А1 и пунктов назначения В3. Потребности В3 больше оставшихся запасов пункта А1. Положим 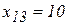 и исключим из рассмотрения строку А1. Значение
и исключим из рассмотрения строку А1. Значение 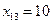 записываем в клетку (1,3) и считаем потребности пункта В3 равными 110 единиц.
записываем в клетку (1,3) и считаем потребности пункта В3 равными 110 единиц.
Переходим к заполнению клетки (2,3) и т.д. Через шесть шагов остается один пункт отправления А3 с запасом груза 100 единиц и один пункт назначения В5 с потребностью 100 единиц. Имеется одна клетка (3,5), которую и заполняем 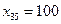 . В результате получили опорный план
. В результате получили опорный план
| Пункт отправления | Пункты назначения | Запасы | ||||
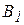
| 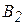
| 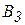
| 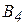
| 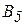
| ||
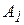
| ||||||

| ||||||
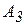
| ||||||
| Потребности |
Клетки таблицы, в которых стоят ненулевые переменные, являются базисными, их число равно 7. Остальные клетки - свободные (пустые), в них стоят нулевые переменные, их число равно 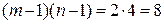 . Условия для опорного плана выполнены.
. Условия для опорного плана выполнены.
Согласно данному плану перевозок, общая стоимость перевозок всего груза составляет
F =2•60+ 3•70 + 4•10 + 1•110 + 4•70 + 7•60 + 2•100 = 1380
Для проверки оптимальности полученного плана воспользуемся методом потенциалов. Введем строку потенциалов 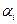 и столбец
и столбец 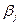 . Полагаем
. Полагаем 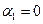 , а остальные
, а остальные 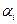 и
и 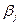 найдем так, чтобы для заполненных клеток выполнялось равенства
найдем так, чтобы для заполненных клеток выполнялось равенства
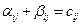 .
.
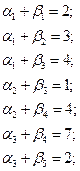
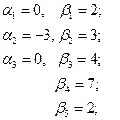
Запишем оценки для пустых клеток и проследим выполнение неравенства 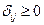 :
:
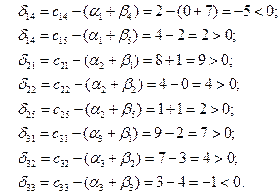
Так как 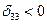 , то составим цикл для клетки (3,3).
, то составим цикл для клетки (3,3).
| Пункт отправления | Пункты назначения | Запасы | ||||
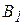
| 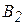
| 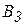
| 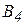
| 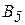
| ||
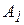
| 10 | |||||
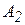
|
  - 110 - 110
|
 + 70 + 70
| ||||
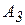
|
 + +
| - 60 | ||||
| Потребности |
Цена цикла составляет 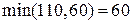 . Составим потенциальный план, перемещая по циклу 60 единиц.
. Составим потенциальный план, перемещая по циклу 60 единиц.
| Пункт отправления | Пункты назначения | Запасы | ||||
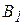
| 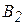
| 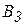
| 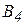
| 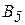
| ||
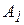
| ||||||
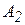
| ||||||
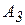
| ||||||
| Потребности |
Согласно новому плану перевозок, общая стоимость перевозок всего груза составляет
F =2•60+ 3•70 + 4•10 + 1•50 + 4•130 + 3•60 + 2•100 = 1320
Проверим оптимален ли полученный план.
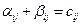 .
.
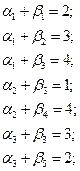
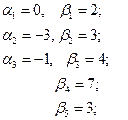
Запишем оценки для пустых клеток и проследим выполнение неравенства 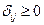 :
:
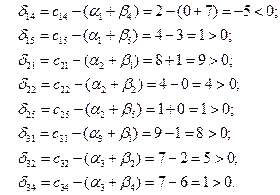
Так как 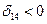 , то составим цикл для клетки (1,4).
, то составим цикл для клетки (1,4).
| Пункт отправления | Пункты назначения | Запасы | ||||
| 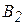
| 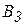
| 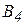
| 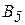
| ||
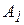
|
  - 10 - 10
|
 + +
| ||||
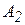
|
 +50 +50
| - 130 | ||||
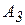
| ||||||
| Потребности |
| Пункт отправления | Пункты назначения | Запасы | ||||
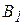
| 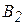
| 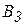
| 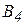
| 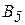
| ||
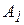
| ||||||
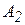
| ||||||
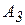
| ||||||
| Потребности |
Согласно новому плану перевозок, общая стоимость перевозок всего груза составляет
F =2•60+ 3•70 + 2•10 + 1•60 + 4•120 + 3•60 + 2•100 = 1270
Проверим оптимален ли полученный план.
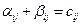 .
.
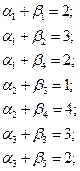
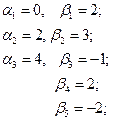
Запишем оценки для пустых клеток и проследим выполнение неравенства  :
:
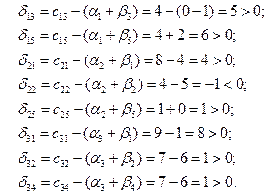
Так как 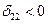 , то составим цикл для клетки (2,2).
, то составим цикл для клетки (2,2).
| Пункт отправления | Пункты назначения | Запасы | ||||
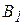
| 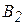
| 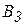
| 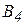
| 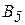
| ||
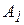
|
  - 70 - 70
|
 + 10 + 10
| ||||
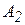
|
 + +
| - 120 | ||||
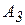
| ||||||
| Потребности |
| Пункт отправления | Пункты назначения | Запасы | ||||
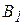
| 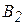
| 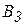
| 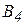
| 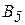
| ||
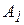
| ||||||
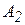
| ||||||
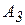
| ||||||
| Потребности |
Согласно новому плану перевозок, общая стоимость перевозок всего груза составляет
F =2•60+ 2•80 + 4•70 + 1•60 + 4•50 + 3•60 + 2•100 = 1200
Проверим оптимален ли полученный план.
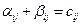 .
.
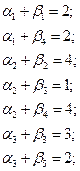
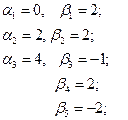
Запишем оценки для пустых клеток и проследим выполнение неравенства 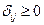 :
:
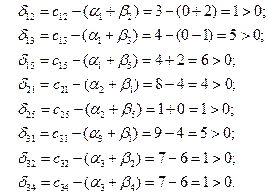
Получили все 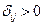 , следовательно, полученный план оптимален и так как
, следовательно, полученный план оптимален и так как 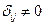 , то он улучшен быть не может.
, то он улучшен быть не может.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 636; Нарушение авторских прав?; Мы поможем в написании вашей работы!