Решение. Этот ряд удовлетворяет условиям теоремы Лейбница, поэтому допускаемая погрешно

Решение

Представим 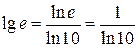Вычислим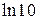

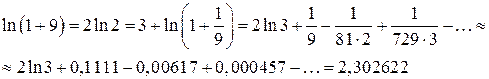
Этот ряд удовлетворяет условиям теоремы Лейбница, поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда, нетрудно видеть, что следующее за 0,000457 значение .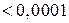

Получим .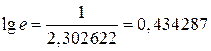

Точное значение функции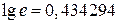

Ответ: .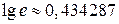

Пример 8. Вычислить приближенно с указанной степенью точности .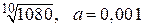

Так как 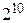ближайшее к 1080 число в десятой степени, то представим

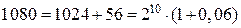или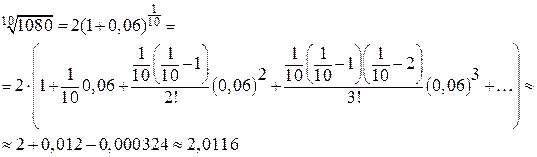

Этот ряд удовлетворяет условиям теоремы Лейбница, поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда, нетрудно видеть, что .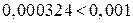

При получении этого разложения воспользовались разложением в ряд Маклорена для функции:

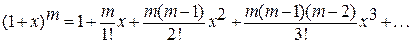при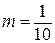

Точное значение выражения .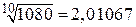

Пример 9. Вычислить определенный интеграл 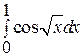с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.

Дата добавления: 2015-07-02