Собственные числа и векторы матрицы, функции матриц

Ортогонализация Грамма-Шмидта

Собственные числа и собственные вектора

Лабораторная работа №10

Цели работы:

· знакомство с функциями нахождения собственных чисел и собственных векторов матрицы;

· разработка алгоритмического и программного обеспечения ортогонализации Грамма-Шмидта.

Необходимое оборудование и материалы.

· ОС Windows XP, Vista, 7;

· Matlab 6.5, 7.x;

· ПК класса не ниже Pentium II, RAM 128Mb.

Трудоемкость: 4 академических часа.

Собственные числа 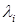и собственные векторы квадратной матрицы 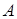удовлетворяют равенствам . Функция eig, вызванная с входным аргументом матрицей, находит все собственные числа матрицы и записывает их в выходной аргумент – вектор:

>> > A=[2 3; 3 5];

lam=eig(A)

lam =

0.1459

6.8541

Для одновременного вычисления всех собственных векторов и чисел следует

вызвать eig с двумя выходными аргументами.

>> [U, Lam]=eig(A)

U =

-0.8507 0.5257

0.5257 0.8507

Lam =

0.1459 0

0 6.8541

Первый выходной аргумент и представляет собой матрицу, столбцы которой являются собственными векторами. Для доступа, например, к первому собственному вектору следует использовать индексацию при помощи двоеточия

>> u1=U(:,1)

u1 =

-0.8507

0.5257

Вторым выходным аргументом Lam возвращается диагональная матрица, содержащая собственные числа исходной матрицы.

Проверьте, правильно ли найдены, например, второе собственное число и соответствующий ему собственный вектор. Воспользуйтесь определением:

>> A*U(:, 2) - Lam(2, 2)*U(:, 2)

ans =

1.0e-015 *

0.4441

-0.8882

Дата добавления: 2015-07-02