Базовый случай фильтра Гаусса

Импульсная характеристика одномерного фильтра Гаусса может быть представлена в виде:

.

А со среднеквадратичным отклонением:

.

Для двумерного случая мы представляем фильтр как произведение двух одномерных случаев, поэтому получим:

.

где x - расстояние от центра по горизонтальной оси, y - расстояние от центра по вертикальной оси, σ - среднеквадратичное отклонение распределения гаусса.

Рассмотрим более общий случай. Результирующая формула будет иметь следующий вид для n-мерного случая:

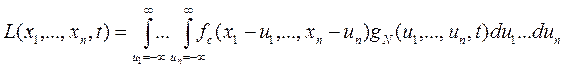
Однако для реализации данное определение может быть нецелесообразным в виду непрерывности. Поэтому в дальнейшем можем сделать некоторые упрощения.

Так как гауссовское ядро обладает свойствами отделимости

,

то n-мерная операция свёртки может быть разбита на множество одномерных применений гауссова ядра для каждого измерения:

, где

.

и где t является корнем дисперсии и равно σ ². Свойство отделимости на практике имеет большое значение, так как позволяет упростить вычисления и привести их к одномерному случаю. Далее будем рассматривать именно его.

Для реализации одномерного шага сглаживания наиболее простым способом является операция свёртки дискретного сигнала и гауссового ядра:

,

где

.

что в свою очередь может быть ограничено для сигнала с конечной импульсной характеристикой:

,

для M выбрано достаточно большим, что:

.

Общий выбор выбора M заключается в создании зависимости её от дисперсии, к примеру:

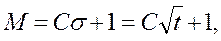
где С зачастую выбирается где-то между 3 и 6.

Использование заданного гауссова ядра может привести к проблемам точности в случаях, когда важны точность и надёжность. При незначительной роли погрешности при вычислениях (10 ^{- 6} до 10 ^{- 8}), ошибки вносимые ограничением ядра незначительны. Однако если точность важна, то есть более лучшие альтернативы гауссову ядру как оконной функции, к примеру, оконные функции Хэмминга, Блэкмана, Кайзера (см. [5]) будут меньше изменять спектр, чем это сделает ядро гаусса. А так как функция Гаусса быстро убывает на концах, то рассматривание значений на 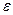больше 10 ^{- 8} не является целесообразным.

Дата добавления: 2015-07-02