
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рекурсивный фильтр Гаусса
|
|
|
|
Существует также ещё один метод фильтрации, основанный на аппроксимации преобразования Фурье гауссового ядра, который широко изложен в [1]. Покажем основную идею данного метода. Для этого представим экспоненту в виде ряда Тэйлора, тогда ядро запишется в виде:
 ,
,
где
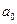 = 2.490895,
= 2.490895,  = 1.466003,
= 1.466003, 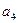 = -0.024393,
= -0.024393,  = 0.178257.
= 0.178257.
Далее мы будем аппроксимировать не само гауссово ядро, а его преобразование Фурье, которое хорошо известно:
 .
.
Тогда, подставляя вместо σ2 - q, мы получим выражение вида:
 .
.
И при s = jw:
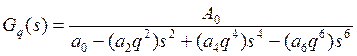 .
.
Тогда выражение (выше), может быть разложено на множители  =
=  *
*  :
:
 .
.
И
 .
.
После этого для представления G (s) в H(z), моно было бы воспользоваться стандартным билинейным преобразованием:
 .
.
Но это бы привело к тому что в передаточной функции появились бы нули, которых нам лучше избежать. Поэтому мы применим технику, описанную в [6] и представим  для
для 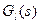 и
и  для
для 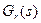 . Принимая T = 1, получим:
. Принимая T = 1, получим:
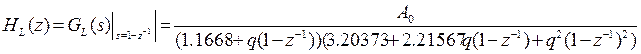 , и
, и
 .
.
Оба выражения могут быть переписаны как стандартные полиномы степени z и  :
:
 ,
,
 , где
, где
 .
.
Тогда реализация [1] советует следующую фильтрующую стратегию. Входные данные сначала фильтруются в прямом направлении согласно выражению для  . Тогда результат этой фильтрации, назовём его w[n], фильтруется в обратном направлении согласно выражению для
. Тогда результат этой фильтрации, назовём его w[n], фильтруется в обратном направлении согласно выражению для  , и разностные выражения принимают следующий вид:
, и разностные выражения принимают следующий вид:
· Прямое:
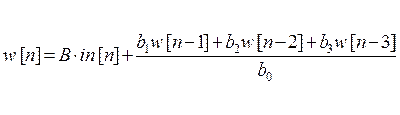 ,
,
· обратное:
 .
.
Оба выражения используют нормализационную константу, которая имеет вид:
 .
.
Стандартные рекомендации по выбору константы q представляют собой:
 .
.
Итого сам фильтр сначала применяется по вертикали, а затем по горизонтали. Средняя погрешность не превышает  , что составляет не более 0.68% согласно [1].
, что составляет не более 0.68% согласно [1].
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 938; Нарушение авторских прав?; Мы поможем в написании вашей работы!