Дискретное преобразование Фурье

Применение фильтра Гаусса с помощью преобразования Фурье

Итак, вспомним, что же такое преобразование Фурье – это интегральное преобразование, которое ставит функцию вещественной переменой другую функцию вещественной переменной и может быть записано в виде:

.

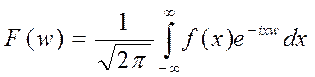Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Не будем перечислять все свойства преобразования, а отметим только важные для нас.

1. Формула обращения позволяет получить искомую функцию

.

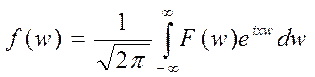2. Теорема о свёртке. Свёртка функций — операция, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. Пусть — две функции вещественной переменной, интегрируемые относительно меры Лебега. Тогда их свёрткой называется функция:

.

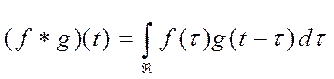Тогда теорема о свёртке гласит: если 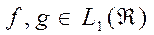, тогда

.

Так как мы работаем с изображениями, то представим перечисленные выше высказывания в дискретном виде. Прямое преобразование примет вид:

.

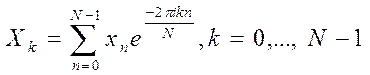Обратное преобразование:

.

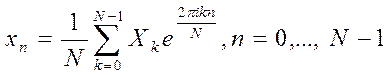Теорема о свёртке:

.

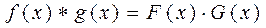Таким образом, мы можем выполнить частотную фильтрацию изображения в частотной области. Это означает, что при частотной фильтрации выполняются прямое и обратное пространственно-частотное преобразование, в нашем случае двумерное дискретное преобразование Фурье (ДПФ) преобразует изображение, заданное в пространственной координатной системе (x, y), в двумерное дискретное преобразование изображения, заданное в частотной координатной системе (u, v). В соответствии с теоремой о свертке, свертка двух функций в пространственной области может быть получена ОДПФ произведения их ДПФ.

Таким образом, алгоритм фильтрации по Гауссу в частотной области будет выглядеть следующим образом:

· выполнить двумерное ДПФ входного изображения f (x,y) (подвергаемого фильтрации) размером (N * M), получить F(u,v);

· вычислить передаточную характеристику фильтра Гаусса в частотной области

,

размер матрицы (N*M); выполнить децентрирование характеристики

H (u,v);

· выполнить поточечное умножение

,

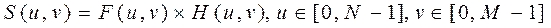· выполнить ОДФП

На практике ДПФ крайне не эффективно, так как имеет сложность O (N ²), поэтому обычно применяют быстрое преобразование Фурье (БПФ).

Дата добавления: 2015-07-02