Примеры ортогональных систем функций

Ортогональная система функций.

Среди функциональных рядов

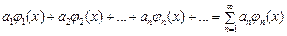(51)

особое место занимают ряды, где в качестве функций используют ортогональные функции.

О1. Функции j(х) и y(х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если

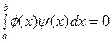(52)

О2. Последовательность функций j₁(x), j₂(x), …, j_n(x),... непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если любые две функции системы попарно ортогональны, т.е., если

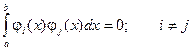(53)

и

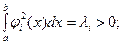(54)

О3. Система функций называется нормальной (ортонормированной), если 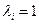, т.е., если

(55)

Замечание. От ортогональной системы всегда можно перейти к ортонормированной .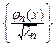

1) Тригонометрическая система функций

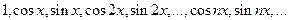(56)

ортогональна на промежутке [-π, π], так как

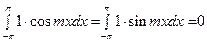; (57)

(58)

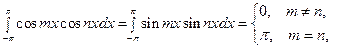; (59)

Ввиду (59) данная система не является нормальной, но умножая функции (56) на соответствующие множители можно получить нормальную систему:

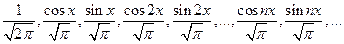(60)

2) Тригонометрические системы функций, состоящие только из косинусов

(61)

либо только из синусов

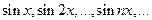(62)

ортогональны на промежутке [0, π].

3) Система функций

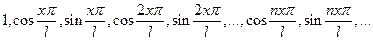(63)

ортогональна на промежутке [-l, l].

4) Системы функций

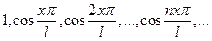(64)

(65)

ортогональны на промежутке [0, l].

Замечание. Системы (56), 61), (62) можно рассматривать как частные случаи систем (63), (64) и (65) соответственно при l=π.

5) Многочлены Лежандра

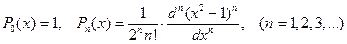(66)

ортогональны на промежутке [-1, 1].

Так как

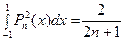, (67)

то для получения нормальной системы полиномы нужно умножить на

(68)

8.16 Разложение функции по ортогональной системе функций. Обобщённый ряд Фурье.

Предположим, что определённая на промежутке [a,b] функция f(x) может быть представлена в виде ряда по системе функций ортогональных на [a,b]:

, (69)

c_i - числовые коэффициенты.

Умножая левую и правую части (69) на 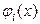, интегрируя полученное равенство по промежутку [a,b] и учитывая свойство ортогональности функций (53), для c_i получаем:

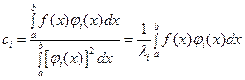(70)

О1. Ряд (69) называется обобщённым рядом Фурье, а коэффициенты, вычисленные по (70) коэффициентами обобщённого ряда Фурье по системе ортогональных на промежутке [a,b] функций .

Дата добавления: 2015-07-02