Смешение идеальных газов при постоянных температуре и давлении

Изотермическое сжатие или расширение идеального газа.

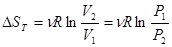(30)

Если n₁ молей одного газа, занимающего объем V ₁, смешиваются с n₂ молями другого газа, занимающего объем V ₂, то общий объем газовой смеси будет равен (V ₁ + V ₂ ). Изменение энтропии в рассматриваемом процессе равно сумме изменений энтропии каждого газа при изменении его объема от первоначального значения до(V ₁ + V ₂ ):

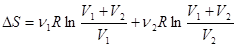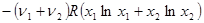= (31)

- мольная доля i -го газа в полученной газовой смеси. Изменение энтропии при смешении газов всегда положительно, так как все ln x_i < 0, поэтому идеальные газы всегда смешиваются необратимо. Если при тех же условиях смешиваются два разных объема одного и того же газа, то уравнение (48) уже неприменимо. Никаких изменений в системе при таком смешении не происходит, и S = 0. Тем не менее, формула (48) не содержит никаких индивидуальных параметров газов, поэтому, казалось бы, должна быть применима и к смешению одинаковых газов. Это противоречие называют парадоксом Гиббса.

5) Постулат Планка. Абсолютные значения энтропии.

Для энтропии характерна шкала абсолютных значений, в основе которой лежит тепловая теорема Нернста и постулат Планка (третий закон термодинамики). Тепловая теорема Нернста: вблизи абсолютного нуля температур все процессы протекают без изменения энтропии.

Постулат Планка: энтропия идеального кристаллического вещества равна нулю при абсолютном нуле температур .

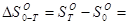
(32)

- абсолютная энтропия некоторого вещества при температуре Т (стандартное значение).

Для расчета абсолютной энтропии веществ в стандартном состоянии надо знать зависимости теплоемкости C_p от температуры для каждой из фаз, а также температуры и энтальпии фазовых переходов. Так, например, абсолютная энтропия газообразного вещества в стандартном состоянии при температуре T складывается из следующих составляющих:

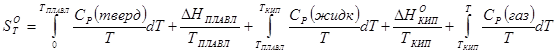(33)

В термодинамических таблицах приводят значения абсолютных энтропий веществ в стандартном состоянии при температуре 298 К.

6) Изменения энтропии при химических реакциях.

Значения абсолютной энтропии веществ используют для расчета изменения энтропии в химических реакциях. Изменение энтропии при химической реакции равно разности абсолютных значений энтропий продуктов реакции (i) и исходных веществ (j) с учетом стехиоетрических коэффициентов.

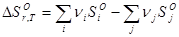(34)

Пример 4. Вычислить изменение энтропии для реакции С₂Н₂ + 2 Н₂ = С₂Н₆ в стандарт

ных условиях при температуре 298 К.

Решение: В справочнике находим значения абсолютных энтропий участников реакции при температуре 298 К:

С₂Н₂ Н₂ С₂Н₆

кал/моль К 48,00 31,21 54,85

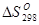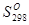= (С₂Н₆) - 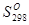(С₂Н₂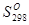) - 2 (Н₂)

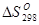= 4,85 – 48,00 - 2×31,21 = - 5,7 кал/моль К

Физический смысл энтропии.

Вариант 1 (термодинамический). Из термодинамического определения энтропии следует равенство 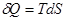. Выражение 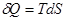позволяет сделать вывод, что процесс выравнивания температуры системы (фактора интенсивности) должен сопровождаться изменением фактора емкости, роль которого выполняет энтропия.

Вариант 2 (молекулярно-кинетический). Энтропия – мера беспорядочности движения молекул. Энтропия возрастает при увеличении «беспорядочности», хаотичности движения молекул (при нагревании, плавлении, испарении вещества, увеличении объема газов).

Вариант 3 (статистический). Статистическое определение энтропии основано на идее о том, что необратимые процессы в термодинамике вызваны переходом в более вероятное состояние, поэтому энтропию можно связать с термодинамической вероятностью состояния систем. Термодинамическая вероятность состояния систем W определяет число микросостояний, которыми может быть реализовано данное макросостояние системы. Если, например, система объема V состоит из двух равных по объему частей, содержит в целом N молекул, которые так распределены в системе, что в одной половине сосуда находится N₁ молекул, в другой половине сосуда находится N₂ = N – N₁ молекул, то число микросостояний (возможных распределений «разных» молекул), которыми реализуется такое распределение – макросостояние, определяется по формуле:

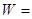N!/ N₁! × (N – N₁)! (35)

Наибольшим числом способов реализуется равномерное распределение молекул в системе, которое соответствует равновесному состоянию. Этот вывод справедлив для систем, состоящих из большого числа частиц. Максимум энтропии также соответствует равновесному состоянию системы. Связь между энтропией и термодинамической вероятностью состояния систем была установлена Больцаном:

Формула Больцмана: 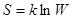(36)

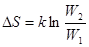(37)

где k = 1.38 10^-23 Дж/К - постоянная Больцмана (k = R / N _A), W - термодинамическая вероятность состояния системы, т.е. число микросостояний, которые соответствуют данному макросостоянию системы.

Наибольшее значение W соответствует равновесному состоянию системы. Соотношение (54) показывает, что возрастание энтропии соответствует переходу системы к состоянию с большей термодинамической вероятностью.

В реальных макросистемах небольшие отклонения от равномерного распределения частиц имеют место и происходят очень часто. Такие отклонения называют флуктуациями. Флуктуации - самопроизвольные процессы, отдаляющие систему от равновесия. С позиции второго начала термодинамики процессы, отдаляющие систему от равновесия, не могут протекать самопроизвольно. Следовательно, второе начало термодинамики не является всеобщим законом природы. Оно выполняется с высокой точностью только для систем, состоящих из большого числа частиц, т.е. является законом статистическим.

Дата добавления: 2015-07-02