Критерии подобия. Требования к проведению эксперимента

Для обеспечения возможности пересчета полученных данных с модели на натуру, необходимо выполнить три вида подобия: геометрическое, кинематическое и динамическое.

Геометрическое подобие определяет пропорциональность линейных раз-меров модели и натуры, т.е. модель должна быть выполнена строго в определенном масштабе по отношению к натуре:

. (6.1)

Кинематическое подобие характеризуется пропорциональностью значений скоростей в сходственных точках потока.

Динамическое подобие подразумевает пропорциональность сил различной физической природы у модели и натуры. Для обеспечения полного динамического подобия необходимо выполнить одновременное равенство следующих критериев подобия, определенных для модели и натуры:

· числа Струхаля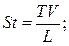

· числа Фруда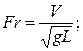

· числа Эйлера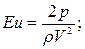

· числа Рейнольдса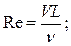

· числа Вебера .

В этих выражениях L – характерная длина; Т – характерное время; V – характерная скорость; p – давление в жидкости; g – ускорение свободного падения; r - плотность жидкости; s_П – коэффициент сил поверхностного натяжения.

Рассмотрим эти критерии применительно к модельным испытаниям качки.

Число Струхаля St связано с неустановившимся или периодическим движением жидкости, поэтому при моделировании качки оно должно обязательно учитываться. Условие моделирования по числу Струхаля будет иметь вид:

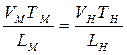, (6.2)

где за характерный период времени обычно принимают период собственных колебаний на тихой воде.

Число Эйлера Eu связано с силами гидродинамического давления. Этот критерий подобия имеет самостоятельное значения только при моделиро-вании кавитации. А так как в процессе качки кавитация может возникнуть лишь в весьма частном случае перекладки бортовых управляемых рулей, то моделирование по этому критерию не производят.

Важнейшим динамическим критерием подобия в модельных экспериментах по качке является число Фруда, которое характеризует отношение инер-ционных сил в жидкости к силе тяжести. Число Fr определяет, в первую очередь, моделирование процесса волнообразования при движении судна по поверхности воды. Равенство чисел Фруда модели и натуры обеспечивает пропорциональность волновых гидродинамических сил. Для этого необхо-димо, чтобы:

. (6.3)

Отсюда скорость модели будет равна

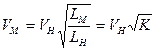. (6.4)

Используя число St, получим период волны или период качки для модели

, (6.5)

т.е. при соблюдении условий подобия одновременно по St и по Fr период качки модели, замеренный в процессе испытаний, должен быть меньше периода качки натурного корабля в число раз, равное корню квадратному из масштабного коэффициента.

Моделирование по числу Рейнольдса характеризует отношение сил инерции к силам вязкости. При моделировании качки это прежде всего силы трения воды о наружную обшивку корпуса и сопротивление формы при отрывном обтекании и вихреобразовании (например, на скуловых килях). Равенство чисел Рейнольдса модели и натуры подразумевает пропорциональность гидродинамических сил, обусловленных вязкостью жидкости, у модели и натуры:

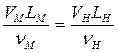. (6.6)

При испытаниях в воде кинематические коэффициенты вязкости модели и натуры принимают равными . Тогда

. (6.7)

В условиях модельных испытаний качки последнее соотношение выпол-нить невозможно, поэтому подобие по числу Рейнольдса не выполняется и силы вязкостной природы не моделируются. Однако известно, что при движении тел в жидкости существует так называемая зона автомодельности, в которой безразмерные коэффициенты гидродинамических сил и моментов практически не зависят от числа Рейнольдса. Многочисленными опытами установлено, что автомодельность при испытаниях качки обеспечивается, если число будет порядка Re = 10⁶, во всяком случае, оно должно быть не меньше . Чтобы достичь таких чисел Re при бортовой качке моделей, иногда приходится значительно увеличивать размеры моделей.

Число Вебера We характеризует отношение сил поверхностного натяжения к силам инерции жидкости. Равенство чисел Вебера модели и натуры приводит к условию

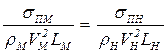. (6.8)

Принимая 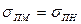и 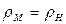, получим

. (6.9)

Это условие в процессе модельных испытаний на качку выполнить также невозможно. В суммарном гидродинамическом моменте, действующем на натурный корабль, роль момента сил поверхностного натяжения всегда ничтожна, в то время как для моделей она может быть значительной (от 40% на малой модели и до 16% на сравнительно большой). Для уменьшения погрешности рекомендуется при испытаниях на бортовую качку ширину моделей принимать не меньше 0,5 метров.

Таким образом, при моделировании процесса качки необходимо осуществ-лять подобие по числам Струхаля и Фруда, добиваться 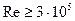и использовать модели, ширина которых B > 0,5 м. При модельных испытаниях на продольную качку последние два ограничения не нужны, так как влияние вязкостных сил и сил поверхностного натяжения незначительны. Однако длину моделей рекомендуется принимать не меньше 1,5 метров.

Дата добавления: 2015-07-02