
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример расчета бортовой качки судна на регулярном волнении
|
|
|
|
Исходные размеры и параметры судна: L = 90 м; B = 12,85 м; T = 3,88 м; H = 7,44 м; d = 0,65; a = 0,747; zс = 2,07 м; r = 3,6 м; h0 =1,44 м; zg = 3,994 м.
Момент инерции массы корпуса, рассчитанный по формуле Шиманского, Jх =50970 тм2.
Собственная частота бортовой качки, рассчитанная по формуле (6.29), 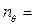 =0,823 1/c.
=0,823 1/c.
Коэффициенты демпфирования и момента инерции присоединенных масс, определенные по номограммам, 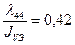 ;
; 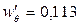 . По формулам (6.37) и (6.40) рассчитываем
. По формулам (6.37) и (6.40) рассчитываем 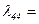 11400 тм2;
11400 тм2; 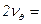 0,096 1/c.
0,096 1/c.
Таблица 6.3. Расчет бортовой качки на регулярном волнении
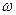
| 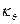
| 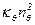
| 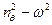
|
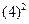
| 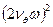
| 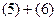
| 
| 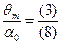
| 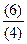
| 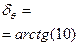 гго((град гго((град
|
| 0,1 | 0,995 | 0,674 | 0,667 | 0,445 | 0,445 | 0,667 | 1,009 | 0,014 | 0,82 | |
| 0,2 | 0,979 | 0,663 | 0,637 | 0,406 | 0,406 | 0,638 | 1,04 | 0,03 | 1,72 | |
| 0,3 | 0,953 | 0,645 | 0,587 | 0,345 | 0,001 | 0,346 | 0,588 | 1,098 | 0,049 | 2,8 |
| 0,4 | 0,918 | 0,621 | 0,517 | 0,268 | 0,001 | 0,269 | 0,519 | 1,198 | 0,074 | 4,24 |
| 0,5 | 0,874 | 0,592 | 0,427 | 0,183 | 0,002 | 0,185 | 0,43 | 1,377 | 0,112 | 6,4 |
| 0,6 | 0,824 | 0,558 | 0,317 | 0,101 | 0,003 | 0,104 | 0,322 | 1,731 | 0,181 | 10,28 |
| 0,7 | 0,769 | 0,52 | 0,187 | 0,035 | 0,005 | 0,04 | 0,199 | 2,617 | 0,358 | 19,72 |
| 0,8 | 0,709 | 0,48 | 0,037 | 0,001 | 0,006 | 0,007 | 0,085 | 5,632 | 2,06 | 64,11 |
| 0,9 | 0,647 | 0,438 | -0,133 | 0,018 | 0,007 | 0,025 | 0,158 | 2,768 | -0,65 | 146,98 |
| 0,584 | 0,396 | -0,323 | 0,104 | 0,009 | 0,113 | 0,337 | 1,175 | -0,297 | 163,46 | |
| 1,1 | 0,522 | 0,353 | -0,533 | 0,284 | 0,011 | 0,295 | 0,543 | 0,651 | -0,198 | 168,8 |
| 1,2 | 0,461 | 0,312 | -0,763 | 0,582 | 0,013 | 0,595 | 0,771 | 0,405 | -0,151 | 171,42 |
| 1,3 | 0,403 | 0,273 | -1,013 | 1,026 | 0,016 | 1,041 | 1,02 | 0,268 | -0,123 | 172,98 |
| 1,4 | 0,349 | 0,236 | -1,283 | 1,646 | 0,018 | 1,664 | 1,29 | 0,183 | -0,105 | 174,03 |
| 1,5 | 0,299 | 0,202 | -1,573 | 2,474 | 0,021 | 2,494 | 1,579 | 0,128 | -0,091 | 174,78 |
| 1,6 | 0,253 | 0,171 | -1,883 | 3,545 | 0,024 | 3,568 | 1,889 | 0,091 | -0,081 | 175,34 |
| 1,7 | 0,212 | 0,143 | -2,213 | 4,896 | 0,027 | 4,923 | 2,219 | 0,065 | -0,074 | 175,79 |
| 1,8 | 0,175 | 0,119 | -2,563 | 6,568 | 0,03 | 6,598 | 2,569 | 0,046 | -0,067 | 176,15 |
| 1,9 | 0,144 | 0,097 | -2,933 | 8,601 | 0,033 | 8,634 | 2,938 | 0,033 | -0,062 | 176,45 |
| 0,117 | 0,079 | -3,323 | 11,04 | 0,037 | 11,078 | 3,328 | 0,024 | -0,058 | 176,7 |

Рис. 6.19 Амплитудно-частотная характеристика бортовой качки

Рис. 6.20 Фазово - частотная характеристика бортовой качки
6.3.2. РАСЧЕТ БОРТОВОЙ КАЧКИ КОРАБЛЯ НА НЕРЕГУЛЯРНОМ ВОЛНЕНИИ
Расчет любого вида качки, в том числе и бортовой, на нерегулярном волнении основан на применении формулы Хинчина, устанавливающей связь между спектральной плотностью входного процесса (волнения) и спектральной плотностью выходного процесса (качки):
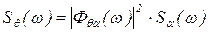 , (6.47)
, (6.47)
где
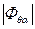 -модуль передаточной функции, равный коэффициенту динамичности качки на регулярном волнении
-модуль передаточной функции, равный коэффициенту динамичности качки на регулярном волнении
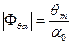 ; (6.48)
; (6.48)
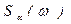 - спектральная плотность уклонов волнения.
- спектральная плотность уклонов волнения.
Расчет спектральной плотности бортовой качки на нерегулярном волнении проводится в следующей последовательности.
1) Для расчета спектра волнения используется формула Вознесенского - Нецветаева:
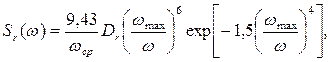 (6.49)
(6.49)
где
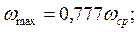
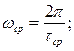
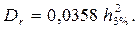
Здесь 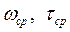 - средние частота и период морского нерегулярного волнения;
- средние частота и период морского нерегулярного волнения;
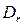 - дисперсия ординат волнового профиля.
- дисперсия ординат волнового профиля.
Высоту волны трехпроцентной обеспеченности 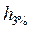 определяем по шкале балльности волнения Главного управления гидрометеорологической службы (ГУГМС), выбирая для заданной балльности ее максимальное значение из таблицы 6.4.
определяем по шкале балльности волнения Главного управления гидрометеорологической службы (ГУГМС), выбирая для заданной балльности ее максимальное значение из таблицы 6.4.
Таблица 6.4
| Балл | I | II | III | IY | Y | YI | YII | YIII | IX |
Высота волны 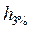 , (м) , (м)
| До 0,25 | 0,25-0,75 | 0,75-1,25 | 1,25-2 | 2-3,5 | 3,5-6 | 6-8,5 | 8,5-11 | >11 |
Для выбора расчетных значений средних периодов 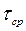 используем таблицу 6.5.
используем таблицу 6.5.
Таблица 6.5
| Балл | I | II | III | IY | Y | YI | YII | YIII | IX |
Средний период 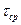 (сек) (сек)
| 1-2 | 2-3 | 3-4 | 4-5 | 5-7 | 7-9 | 9-11 | 11-12 | >12 |
Спектральная плотность уклонов волнения 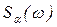 связана со спек-тральной плотностью ординат волнения
связана со спек-тральной плотностью ординат волнения 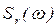 следующей зависимостью:
следующей зависимостью:
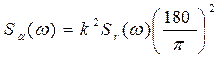 , (6.50)
, (6.50)
где 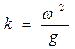 - волновое число.
- волновое число.
2) Используя значения коэффициентов динамичности, вычисленных по формулам (6.34) в качестве передаточных функций и подставляя их в (6.46), найдем спектральную плотность угловых перемещений при бортовой качке 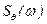 .
.
Спектральные плотности скоростей и ускорений вычисляются по следующим формулам:
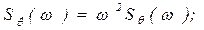 (6.51)
(6.51)
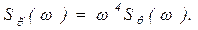 (6.52)
(6.52)
3) Для определения дисперсий угловых перемещений, скоростей и ускорений используем известные формулы связи между дисперсиями и спектрами:
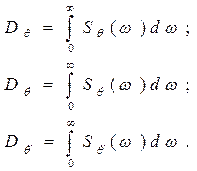 (6.53)
(6.53)
Применяя правило трапеций для определения интегралов, входящих в (6.53) и учитывая, что при w ® 0 и при w ® ¥ 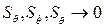 , получим
, получим
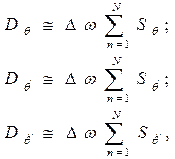 (6.54)
(6.54)
где N –количество расчетных частот.
4) Зная значения дисперсий можно определяем все статистические характе-ристики бортовой качки по следующим формулам:
· средние амплитуды качки (обеспеченность 45,6%)
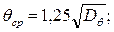 (6.55)
(6.55)
· амплитуды 3% обеспеченности
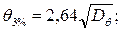 (6.56)
(6.56)
· максимальные амплитуды (обеспеченность 0,5%)
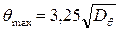 ; (6.57)
; (6.57)
· амплитудные значения скоростей
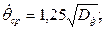
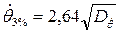 ; (6.58)
; (6.58)
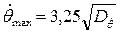 ;
;
· амплитудные значения ускорений определяются соответственно через дисперсии 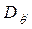 по аналогичным формулам:
по аналогичным формулам:
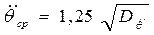 ;
;
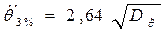 ; (6.59)
; (6.59)
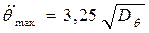 .
.
Расчет бортовой качки корабля проводится для двух балльностей (6 и 8 баллов) в табличной форме (табл. 6.6). По результатам расчетов строятся графики спектральных плотностей волнения и качки для каждого значения балльности (рис. 6.21, 6.22) и приводится таблица статистических характе-ристик (табл. 6.7).
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1587; Нарушение авторских прав?; Мы поможем в написании вашей работы!