
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение характеристик бортовой качки корабля при обработке записей свободных затухающих колебаний
|
|
|
|
КАЧКИ
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
При модельных испытаниях качки корабля применяются два метода – метод свободных колебаний и метод вынужденных колебаний.
Метод свободных колебанийиспользуется при изучении качки на спокой-ной воде с целью определения периода свободных затухающих бортовых колебаний, коэффициента демпфирования бортовой качки и присоединенного момента инерции. Для обеспечения подобия модели и натуры, модель предварительно подвергается тарировке.
Тарировка – это определение параметров модели (вес, положение центра тяжести и т.д.) и приведение их к значениям, обеспечивающим подобие мо-дели и натуры. Тарировка бывает двух видов - статическая и динамическая.
Статическая тарировка модели состоит в установлении веса и положения центра ее тяжести. Вес модели определяется взвешиванием. Положение центра тяжести может быть определено на плаву с помощью «опыта кренования» или в процессе динамической тарировки.
Динамическую тарировку проводят для определения момента инерции. Модель раскачивают в воздухе на специальных ножах и измеряют период свободных колебаний. Затем, используя известную формулу для периода маятника и соотношение между центральным и нецентральным моментами инерции масс, находят:
 (6.10)
(6.10)
где
 - момент инерции массы модели относительно продольной оси Gx;
- момент инерции массы модели относительно продольной оси Gx;
D - весовое водоизмещение;
d = zH - zg;
zH - отстояние оси качания от основной плоскости;
zg – отстояние центра тяжести модели от основной плоскости.
После тарировки приступают непосредственно к испытаниям по методу свободных колебаний. Для определения периода качки, коэффициента демпфирования и присоединенного момента инерции спущенная на воду модель наклоняется экспериментатором на 15-250, затем отпускается и начи-нает совершать свободные затухающие колебания, которые записываются с помощью гирокренографа. Типичная запись для модели транспортного судна изображена на рис. 6.10. При дальнейшей обработке осциллограммы опреде-ляются все необходимые величины.
При большом демпфировании свободные колебания быстро затухают и их обработка сопровождается большими погрешностями. Поэтому при моделировании вертикальной и килевой качки, а также бортовой качки моделей, имеющих развитые выступающие части единственно возможным экспериментальным методом является метод вынужденных колебаний. Суть данного метода заключается в следующем: на модели устанавливают раскачивающее устройство, создающее момент, изменяющийся по гармо-ническому закону
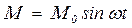 . (6.11)
. (6.11)
Здесь  - частота возмущения.
- частота возмущения.
Во время испытаний синхронно регистрируются возмущающий момент и качка модели, что позволяет при любой частоте определить коэффициенты сопротивления и присоединенной массы. Типичный вид осциллограммы вынужденной качки модели на тихой воде с раскачивающим устройством изображен на рис. 6.4.

Рис. 6.4. Осциллограмма вынужденной качки модели на тихой воде с раскачивающим устройством
В настоящее время применяются следующие типы раскачивающих устройств: гироскопические и вращающиеся твердые грузы.
Прецессионное вращение гирораскачивателя приводит к возникновению гироскопического момента. Возмущающий момент, равный гироско-пическому кренящему моменту, определяется следующей приближенной зависимостью:
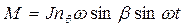 , (6.12)
, (6.12)
где
J - аксиальный момент инерции ротора;
b - установочный угол;
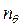 -собственная частота качки модели.
-собственная частота качки модели.
Гирораскачиватели требуют стабилизации напряжения подаваемого тока, так как даже незначительные его колебания приводят к заметным изменениям амплитуды кренящего момента. В последнее время эти раскачиватели не применяются.
Механическая качалка с вращающимися грузами (рис. 6.5) на режимах больших частот работает неустойчиво, что значительно ограничивает сферу применения этого способа раскачивания.

Рис. 6.5. Механическая качалка с вращающимися грузами
Метод вынужденных колебаний применяется не только при испытаниях на тихой воде, но и на волнении. В этом случае раскачивающим устройством служит само регулярное волнение, создаваемое волнопродуктором. Основной целью таких испытаний является определение амплитудно - частотных характеристик различных видов качки.
Построение амплитудного графика является сравнительно простым, но трудоемким экспериментом. Модель многократно испытывается при различных параметрах волнения. Частоты волнения следует изменять с таким расчетом, чтобы охватить во время испытания зону резонансной качки модели.
Во время испытаний регистрируются параметры изучаемых видов качки и создаваемых волнопродуктором волн заданной частоты. Образец записи качки модели на волнении представлен на рис. 6.6. В результате дальнейшей ее обработки строят соответствующую амплитудно - частотную характеристику (рис. 6.7).

Рис. 6.6. Осциллограмма качки модели и характеристик волнения
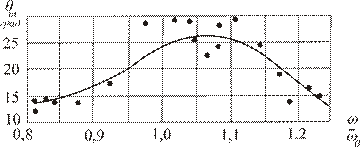
Рис. 6.7. Амплитудно-частотная характеристика модели судна на регулярном волнении
В результате исследования бортовой качки моделей кораблей на тихой воде методом свободных затухающих колебаний можно определить период и частоту собственных колебаний 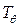 и
и  , безразмерный коэффициент затухания
, безразмерный коэффициент затухания 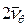 и коэффициент присоединенной массы
и коэффициент присоединенной массы 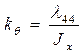 .
.
Перед обработкой осциллограммы свободных затухающих колебаний необходимо определить тарировочный (градуировочный) коэффициент 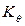 , устанавливающий зависимость между углами наклонения и их размером в миллиметрах на ленте регистрирующего осциллографа. Определение коэф-фициента
, устанавливающий зависимость между углами наклонения и их размером в миллиметрах на ленте регистрирующего осциллографа. Определение коэф-фициента 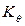 производится на основании тарировочного графика, построен-ного по характерной тарировочной записи (рис. 6.8).
производится на основании тарировочного графика, построен-ного по характерной тарировочной записи (рис. 6.8).
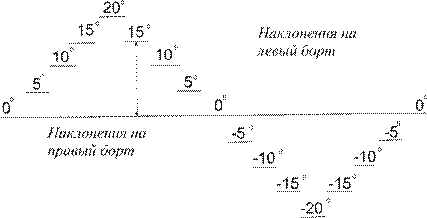
Рис. 6.8 Запись тарировки гировертикали
Для построения тарировочного графика необходимо назаписи измерить отклонения lосц. в миллиметрах от нулевой линии (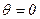 ) при соответствую-щих значениях угла крена q. Затем по полученным значениям надо построить зависимость lосц = f(q). Получаемая зависимость всегда близка к линейной, поэтому ее можно аппроксимировать прямой линией, проходящей через начало координат (рис. 6.9). Уравнение этой прямой имеет вид:
) при соответствую-щих значениях угла крена q. Затем по полученным значениям надо построить зависимость lосц = f(q). Получаемая зависимость всегда близка к линейной, поэтому ее можно аппроксимировать прямой линией, проходящей через начало координат (рис. 6.9). Уравнение этой прямой имеет вид:
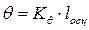 . (6.13)
. (6.13)
 |
Рис. 6.9. Определение тарировочного коэффициента 
Чтобы рассчитать 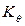 , надо при фиксированном значении q на графике измерить соответствующее значение lосц и взять отношение
, надо при фиксированном значении q на графике измерить соответствующее значение lосц и взять отношение
 . (6.14)
. (6.14)
В приведенном на рис. 6.9 примере при q = 200 lосц = 48,8 мм. Тогда 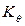 = 0,41 град / мм.
= 0,41 град / мм.
Для определения периода 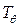 по осциллограмме выполняют следующее:
по осциллограмме выполняют следующее:
1) тщательно проводят огибающие кривые затухающих колебаний;
2) нумеруют через полпериода все амплитудные значения колебаний, кроме начального (рис. 6.10);
3) выделяют n полных колебаний и с помощью вертикальных линий, дающих отсечки времени (тонкие через 0,2 с, жирные – через 2 с) измеряют время Tn этих колебаний (рис.6.10). В рассматриваемом примере количество полных колебаний равно 9;
4) определяют собственный период бортовой качки и собственную частоту как
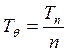 ; (6.15)
; (6.15)
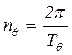 . (6.16)
. (6.16)
Для определения безразмерного коэффициента демпфирования  может быть использована одна из следующих формул:
может быть использована одна из следующих формул:
· формула С.Н. Благовещенского
 , (6.17)
, (6.17)
где
 - разность двух соседних амплитуд;
- разность двух соседних амплитуд;
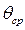 - среднее арифметическое этих же амплитуд;
- среднее арифметическое этих же амплитуд;
· логарифмическая формула
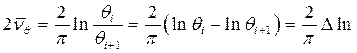 . (6.18)
. (6.18)
Расчет по формуле (6.17) проводится в табличной форме (табл. 6.1) в следующей последовательности:
1) на каждом размахе, начиная с первого снимаются в мм значения размаха liосц как расстояние по вертикали между огибающими (рис. 6.10) и заносятся во II столбец таблицы;
2) вычисляются qi, 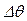 и
и 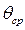
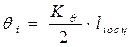 ; (6.19)
; (6.19)
 ; (6.20)
; (6.20)
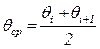 ; (6.21)
; (6.21)
3) по результатам вычислений  строится график
строится график 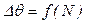 (N -номер размаха). Из-за некоторых погрешностей, имеющих место при проведении эксперимента и снятии liосц, значения
(N -номер размаха). Из-за некоторых погрешностей, имеющих место при проведении эксперимента и снятии liосц, значения  не ложатся на плавную кривую, в связи с чем необходимо провести графическую аппроксимацию зависимости
не ложатся на плавную кривую, в связи с чем необходимо провести графическую аппроксимацию зависимости 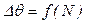 с помощью осредняющей плавной кривой. При этом осредняющая кривая должна убывать при увеличении N (рис. 6.11);
с помощью осредняющей плавной кривой. При этом осредняющая кривая должна убывать при увеличении N (рис. 6.11);
4) в Y столбец заносятся значения 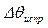 , снятые с аппроксимирующей
, снятые с аппроксимирующей
кривой для каждого размаха (рис. 6.11);
4) в YI столбце вычисляются значения безразмерного коэффициента
демпфирования.
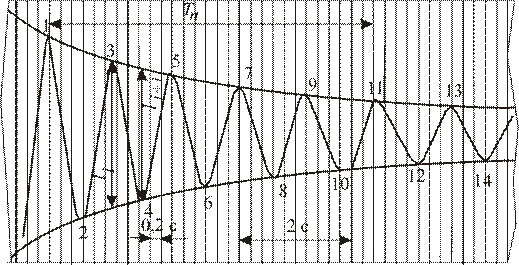
Рис. 6.10. Осциллограмма свободных затухающих колебаний

Рис. 6.11. Аппроксимация зависимости 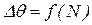
Таблица 6.1. Расчет безразмерного коэффициента затухания по формуле (6.17)
 N N
|  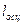
| 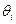
| 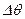
| 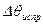
| 
| 
|
| I | II | III | IY | Y | YI | YII |
| 15,58 | - | - | - | - | ||
| 14,76 | 0,82 | 0,94 | 15,17 | 0,0394 | ||
| 13,94 | 0,82 | 0,86 | 14,35 | 0,038 | ||
| 13,12 | 0,82 | 0,8 | 13,53 | 0,0376 | ||
| 12,505 | 0,615 | 0,76 | 12,8125 | 0,0377 | ||
| 11,685 | 0,82 | 0,68 | 12,095 | 0,0357 | ||
| 11,07 | 0,615 | 0,62 | 11,3775 | 0,03469 | ||
| 10,455 | 0,615 | 0,56 | 10,7625 | 0,03312 | ||
| 48,5 | 9,9425 | 0,5125 | 0,52 | 10,198 | 0,03246 | |
| 45,5 | 9,3275 | 0,615 | 0,48 | 9,635 | 0,0317 | |
| 42,5 | 8,7125 | 0,615 | 0,44 | 9,02 | 0,03105 | |
| 8,2 | 0,5125 | 0,41 | 8,456 | 0,0308 | ||
| 37,5 | 7,6875 | 0,5125 | 0,35 | 7,944 | 0,028 | |
| 35,5 | 7,2775 | 0,41 | 0,32 | 7,4825 | 0,0272 | |
| 6,97 | 0,3075 | 0,28 | 7,124 | 0,025 | ||
| 31,5 | 6,4575 | 0,5125 | 0,25 | 6,713 | 0,0237 | |
| 6,15 | 0,3075 | 0,22 | 6,303 | 0,022 | ||
| 5,945 | 0,205 | 0,19 | 6,047 | 0,02 | ||
| 28,5 | 5,8425 | 0,1025 | 0,18 | 5,89 | 0,0194 |
Расчет по коэффициента демпфирования по формуле (6.18) проводится следующим образом (табл. 6.2):
1) вычисляют 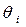 по формуле (6.19),
по формуле (6.19), 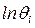 и
и 
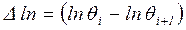 ; (6.23)
; (6.23)
2) строят графическую зависимость 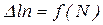 и проводят аппрокси-мирующую кривую (рис. 6.12);
и проводят аппрокси-мирующую кривую (рис. 6.12);
3) в YI столбец заносят значения  , снятые с аппроксимирующей кривой (рис. 6.12);
, снятые с аппроксимирующей кривой (рис. 6.12);
4) вычисляют значения безразмерного коэффициента демпфирования.

Рис. 6.12. Аппроксимация зависимости 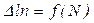
Таблица 6.2. Расчет безразмерного коэффициента затухания по формуле (6.18)

| 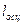 с с
| 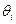
| 
| 
| 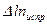
| 
| 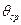
|
| I | II | III | IY | Y | YI | YII | YIII |
| 15,58 | 2,746 | - | - | - | - | ||
| 14,76 | 2,692 | 0,054 | 0,068 | 0,0433 | 15,17 | ||
| 13,94 | 2,635 | 0,057 | 0,066 | 0,042 | 14,35 | ||
| 13,12 | 2,574 | 0,061 | 0,06 | 0,038 | 13,53 | ||
| 12,505 | 2,526 | 0,048 | 0,058 | 0,0369 | 12,8125 | ||
| 11,685 | 2,458 | 0,068 | 0,056 | 0,0356 | 12,095 | ||
| 11,07 | 2,404 | 0,054 | 0,054 | 0,0343 | 11,3775 | ||
| 10,455 | 2,347 | 0,057 | 0,052 | 0,033 | 10,7625 | ||
| 48,5 | 9,9425 | 2,297 | 0,05 | 0,05 | 0,0318 | 10,198 | |
| 45,5 | 9,3275 | 2,233 | 0,064 | 0,048 | 0,0305 | 9,635 | |
| 42,5 | 8,7125 | 2,165 | 0,068 | 0,046 | 0,0292 | 9,02 | |
| 8,2 | 2,104 | 0,061 | 0,044 | 0,028 | 8,456 | ||
| 37,5 | 7,6875 | 2,0396 | 0,0644 | 0,042 | 0,0267 | 7,944 | |
| 35,5 | 7,2775 | 1,9847 | 0,0549 | 0,04 | 0,0254 | 7,4825 | |
| 6,97 | 1,9416 | 0,0431 | 0,038 | 0,024 | 7,124 | ||
| 31,5 | 6,4575 | 1,865 | 0,0766 | 0,036 | 0,0229 | 6,713 | |
| 6,15 | 1,816 | 0,049 | 0,034 | 0,0216 | 6,303 | ||
| 5,945 | 1,7825 | 0,0335 | 0,032 | 0,0203 | 6,047 | ||
| 28,5 | 5,8425 | 1,765 | 0,0175 | 0,03 | 0,019 | 5,89 |
Результаты вычисления безразмерного коэффициента демпфирования по каждой из формул представляются графически в виде зависимости 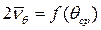 (рис. 6.13). Обычно результаты обработки по обеим формулам очень близки.
(рис. 6.13). Обычно результаты обработки по обеим формулам очень близки.
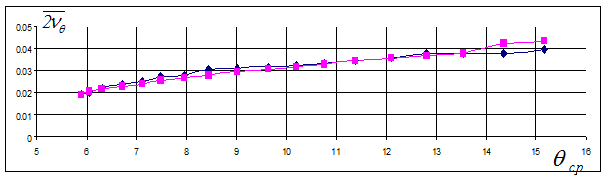
Рис. 6.13 Значения коэффициента затухания, полученные по формулам (6.17) и (6.18)
В практических расчетах качки иногда требуется знать коэффициент квадратичного сопротивления 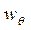 . Для его определения используется сле-дующая формула:
. Для его определения используется сле-дующая формула:
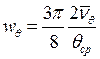 , (6.25)
, (6.25)
полученная из условия равенства работ линейного и квадратичного моментов сопротивления качке за четверть периода.
Для вычисления коэффициента присоединенной массы используется формула:
 . (6.26)
. (6.26)
Напоминаем, что
Jx - момент инерции массы корпуса;
D - весовое водоизмещение модели;
h0 - начальная метацентрическая высота модели;
 - замеренный по осциллограмме период.
- замеренный по осциллограмме период.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 2193; Нарушение авторских прав?; Мы поможем в написании вашей работы!