Оптимальные коды Рида – Соломона

Из (2.8) для следует, что выбор не является принципиальным в рассматриваемой постановке задачи, поэтому полагаем 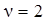. В этом случае символы кодовой последовательности принимают значения из поля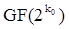

(2.13)

и выбор объема алфавита ШПС однозначно задает длину кода. Подставляя (2.13) в (2.12), получаем

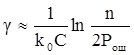. (2.14)

Вычислив значения , при которых эквивалентная вероятность ошибки двоичный информационный символ не превышает значения , по точной формуле (2.6); подставив его в (2.14), находим зависимости от С для всех РС-кодов длиной n=7, 15, 31 и некоторых РС- кодов длиной n=63. значения при рассчитанных кодов представлены в табл. 2.1 и на рис. 2.3. Из кривых на рисунке видно, что для всех n существует оптимальный код, позволяющий реализовать минимальную полосу частот приемника при заданных скоростях передачи информации W и отношении 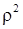на его входе. Оптимальные коды являются высокоскоростными. При скоростях кодов зависимость от С слабо выражена, поэтому можно воспользоваться любым кодом, если увеличение , которое в этом случае незначительно, не играет существенной роли. При низкоскоростных кодах 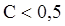параметр резко возрастает, поскольку возрастает избыточность кода.

Таблица 2.1. Параметры корректирующих кодов и ШПС

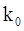
	(n,k,r) - код
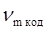
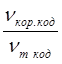
	(7,5,1) (7,3,2) (7,1,3)   (15,13,1) (15,11,2) (15,9,3) (15,7,4) (15,5,5) (15,3,6) (15,1,7)   (31,29,1) (31,27,2) (31,25,3) (31,23,4) (31,21,5) (31,19,6) (31,17,7) (31,15,8) (31,13,9) (31,11,10) (31,9,11) (31,7,12) (31,5,13) (31,3,14) (31,1,15)   (63,61,1) (63,59,2) (63,57,3) (63,55,4) (63,53,5) (63,51,6) (63,49,7) (63,47,8) (63,45,9) (63,43,10) (63,31,16) (63,15,24) (63,1,31)	2,837 3,702 9,910   2,002 1,976 2,138 2,504 3,253 5,128 14,929   1,676 1,568 1,545 1,563 1,616 1,719 1,849 2,027 2,262 2,596 3,089 3,853 5,248 8,702 25,979   1,516 1,410 1,363 1,338 1,331 1,335 1,349 1,371 1,394 1,428 1,789 3,385 48,522	3,301   2,649   2,258   1,997	0,849 1,121 3,002   0,765 0,746 0,807 0,945 1,228 1,936 5,636   0,742 0,694 0,684 0,692 0,716 0,761 0,819 0,898 1,002 1,150 1,368 1,597 2,324 3,854 11,505   0,759 0,706 0,683 0,670 0,666 0,669 0,676 0,687 0,698 0,715 0,856 1,695 24,297	1,305 3,493   1,013 1,082 1,267 1,646 2,595 7,555   1,085 1,015 1,012 1,046 1,113 1,197 1,312 1,464 1,680 1,999 2,494 3,397 5,632 16,815   1,139 1,059 1,024 1,005 1,003 1,014 1,030 1,047 1,073 1,344 2,543 36,455

Чтобы показать, что применение корректирующего кодирования дает выигрыш в полосе частот, сравним рассматриваемую систему связи с аналогичной системой без кодирования. В случае системы связи без кодирования каждый m – ичный символ непосредственно модулируется ортогональным ШПС и передается по каналу связи. Из (2.7)

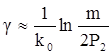. (2.15)

Значение 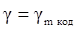, рассчитанные по (2.15) для ,также даны в таблице. Зависимость от 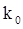(числа ШПС) представлена на рис. 2.4, кривой 2; кривая 1 – зависимость, в которой применены оптимальные коды (7, 5, 1), (15, 11, 2), (31, 25, 3), (63, 53, 5). Как видим, применение оптимальных кодов позволяет получить существенный выигрыш в полосе частот по сравнению с аналогичной системой без кодирования. Данные табл. 2.1 показывают, что не всякий код уменьшает полосу частот. Использование кодов с низкими скоростями передачи требует расширения полосы частот и поэтому нецелесообразно в системах связи с ШПС. Вместе с тем необходимо отметить существование оптимальных кодов минимизирующих полосу частот и обеспечивающих выигрыш в полосе частот по сравнению с m – ичным кодированием.

Дата добавления: 2015-07-02