Использование кодирования в помехоустойчивой аппаратуре

Используются два основных вида кодов, а именно, блочные и сверточные коды. В блочном коде В(n,k) из общего числа n битов только k битов являются информационными. Скорость кода R_к есть число информационных битов, отнесенных к общему числу битов в блоке:

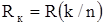(3.6)

В сверточном коде C(n,k) k информационных битов, поступающих на вход декодера, преобразуются в блок из n битов на выходе. В этом случае скорость кода

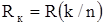(3.7)

Скорости кода, определяемые по (3.6) и (3.7), линейно-пропорциональны информационной скорости R_к. Другим важным параметром кодирования является энергетический выигрыш кодирования (ЭВК), который может быть определен так:

ЭВК=(E_b/h₀)_{без кодирования} - (E_b/h₀)_{с кодированием},

где ЭВК – в децибелах; E_b – средняя энергия на бит; h₀ – плотность мощности шума. Связь между E_b/h₀ и отношением сигнал-шум следующая:

с/ш = P_c / N₀ = E_bR / h₀B,

где P_c – мощность несущей; N₀ – мощность шума; R – скорость передачи информации; В – ширина полосы частот сигнала.

Сравнение величин E_b/h₀ с кодированием и без кодирования для заданной вероятности ошибки позволяет определить ЭВК, которая обычно составляет 4…5 дБ.

При организации связи между ПО в среде с замираниями ошибки возникают в результате смешивания полезного сигнала с гауссовским шумом. Следовательно, необходимо использовать корректирующие коды, такие как код БЧХ, код Рида-Соломона (двоичный и m-ичный), сверточный и перемежающийся блочные коды.

Перед определением вероятности ошибки в кодовом слове и ЭВК кодированного сигнала необходимо определить характеристики быстрых и медленных замираний. Любые два совместно передаваемых бита информации, разделенные в пространстве приблизительно на 0,75l или более, являются некоррелированными. Рассмотрим предельную ситуацию, когда ПО движется со скоростью 112,5 км/ч, и определим число битов S, располагающихся во временном интервале, соответствующем 0,75l, за пределами которого первый бит и S последующих битов некоррелированы. В случае медленных и быстрых замираний и при использовании кодирования можно определить размер кодового блока С сравнением с числом коррелированных битов S: С<<S – случай медленных замираний, первый и последующие кодовые блоки сильно коррелированы.

Рассмотрим корректирующий код Рида-Соломона [РС код (Nk)], используемый в системах с некогерентной ЧМ сигналом.

Двоичный РС код. В таком коде каждые три последующих бита образуют кодовый блок 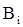(где i = 1,…,8), представляющий собой одну из восьми (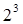) возможных кодовых комбинаций. Кодовое слово РС кода (7,3) формируется из трёх последовательно расположенных информационных блоков с прибавлением к ним четырех проверочных блоков. Одно кодовое слово РС кода состоит из 21 бита или семи кодовых блоков 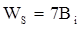, и в нем содержится девять информационных и 12 проверочных бит.

Случай медленных замираний. Допустим, что при медленных замираниях вероятность ошибки в кодовом слове для всех битов может быть принята такой же, как для отдельных битов. Тогда необходимо определить вероятность одной ошибки в каждой группе из трех битов в случае без замираний и таким образом вычислить вероятность ошибки для кодового блока:

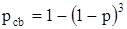, (3.8)

где p – вероятность ошибки в бите некогерентного ЧМ сигнала. Вероятность ошибки в кодовом слове, состоящем из N кодовых битов и исправляющем ошибки в t кодовых блоках:

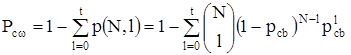, (3.9)

где p(N,l) – вероятность ошибки точно в t кодовых блоках в слове из N кодовых блоков. Тогда усредненная вероятность ошибки в кодовом слове из N кодовых блоков может быть получена из (3.8):

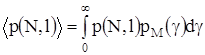, (3.10)

где p_M(g) – соответствует М-канальному устройству выбора максимального отношения сигнал-шум. Вероятность p(N,l) для t ошибок

В (3.11) только p является функцией g; поэтому, подставляя (3.11) в (3.10), получим:

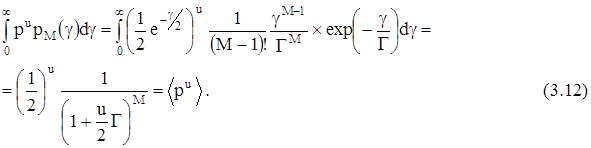
Усредненная вероятность ошибки в кодовом слове для среды с замираниями в системе с М разнесенными каналами может быть вычислена интегрированием выражения (3.9):

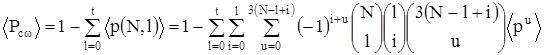, (3.13)

где N=7; t=2; M – число каналов разнесения; Г – элементарное отношение с/ш.

Поскольку код из 21 бита содержит девять информационных битов, то скорость кода равна (9/21)R. Обычно скорость передачи информации эквивалентна полосе передаваемых частот В; отсюда Г=E_b/h₀. Выражение (3.13) иллюстрируется рис. 3.2. Если слово состоит из девяти информационных битов и кодирование отсутствует, то вероятность ошибки в слове в случае медленных замираний

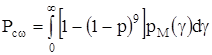, (3.14)

где p – вероятность ошибки в бите для некогерентного ЧМ сигнала; p_M(g) – ФПВ устройства выбора максимального отношения сигнал-шум.

Сравнение сигналов с кодированием и без кодирования для М=1 показывает наличие ЭВК, равного 3 дБ, при вероятности ошибки в кодовом слове, не превышающей 10^-1. Отсюда же следует, что использование разнесенного приема более эффективно, чем использование кодирования.

Если вероятность ошибки в бите определяется при действии К преднамеренных помех (К<m), помеховая обстановка определяется следующим образом:

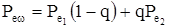. (3.15)

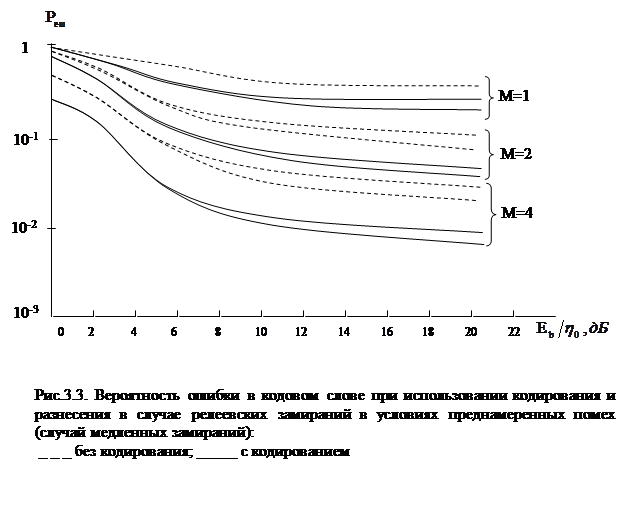
Результат усреднения выражения (3.9) при наличии замираний или при использовании (3.13) проиллюстрирован рис. 3.3. На рис. 3.3 использованы следующие значения параметров: К=50, m=2000, g_j=0 дБ и -5 дБ. В случае медленных замираний вероятность ошибки в слове медленно меняется при уменьшении отношения сигнала к сумме преднамеренной помехи и шума g_j от 0 дБ и -5 дБ. Лимитирующее условие, обусловленное действием преднамеренных помех, определяется как возрастание отношения E_b/h₀. Это означает, что использование разнесения более эффективно, чем кодирования.

Список литературы

1. Ли У. Техника подвижных систем связи: Пер. с англ. – М.:Радио и связь, 1985. – 392 с., ил.

2. Варакин Л.Е. Системы связи с шумоподобными сигналами. – М.: Радио и связь, 1985. – 384 с., ил.

Дата добавления: 2015-07-02