Влияние замираний на вероятность ошибки при приеме кодового слова в случае медленных замираний

Среднее значение вероятности ошибки при приеме кодового слова зависит от скорости замираний, которая в свою очередь, является функцией скорости движения объекта V. При изменении V изменяется скорость замираний и соответственно среднее значение вероятности ошибки при приеме кодового слова. Анализ, учитывающий зависимость среднего значения вероятности ошибки при приеме кодового слова от скорости, сложен и трудновыполним. Однако для двух предельных случаев: быстрых и медленных замираний – соответствующее решение может быть получено.

В случае медленных замираний полагают их скорость такой, при которой отношение мощности несущей к мощности шума не изменяется существенно за время, равное длительности кодового слова. Например, если несущая частота 850 МГц, а скорость движения объекта 96 км/ч, то среднее время, когда мощность несущей по крайней мере на 10 дБ ниже среднего уровня и более, составляет 2 мс. При скорости передачи информации 10 кбит/с примерно 20 символов приходится на длительность замирания. При меньших скоростях движения это число двоичных символов, приходящихся на интервал замирания, может быть больше.

(3.1)

В случае медленных замираний можно считать, что все символы кодового слова могут быть приняты с одной и той же вероятностью ошибки, определяемой выражением (3.1). Вероятность того, что в кодовом слове из N символов произойдет точно m ошибок:

(3.2)

Среднее значение вероятности ошибки при приеме кодового слова может быть найдено усреднением p(N,m) в (3.2). В результате вычислений получим:

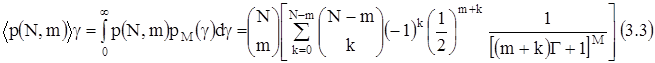
Если корректирующий код не используется, то вероятность ошибочного приема кодового слова

(3.4)

На рис. 3.1 показана зависимость вероятности ошибочного приема кодового слова, вычисленная с помощью выражения (3.4) при N=22 для однократной, двукратной и четырехкратной систем разнесения в условиях медленных замираний. При использовании корректирующего кодирования вероятность ошибочного приема кодового слова уменьшается с увеличением кратности исправляемых ошибок. Тогда выражение (3.4) примет вид:

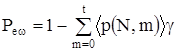(3.5)

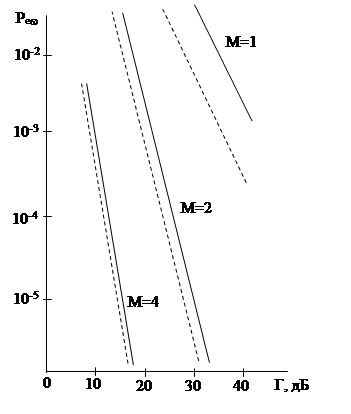Рис. 3.1

Вероятность ошибки при приеме кодового слова (N=22) в условиях быстрых (_____) и медленных (_ _ _) замираний при М-кратном комбинировании ОФМ сигналов, максимизирующем отношение сигнал-шум.

Дата добавления: 2015-07-02