Магнитное поле в веществе

DB

I r

A

Рис.4

Из (1) следует, что величина напряженности магнитного поля в точке, удаленной на расстояние r от элемента тока, равна:

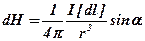, (2)

где 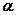- угол между dl и радиус-вектором r, проведенном от элемента тока в рассматриваемую точку А.

Направление вектора напряженности магнитного поля перпендикулярно к dl и r, т.е. перпендикулярно к плоскости, содержащей оба эти вектора. Это направление подчиняется правилу правого буравчика:

направление магнитного поля совпадает с направлением движения конца рукоятки буравчика с правой нарезкой, движущегося поступательно в направлении тока.

Так, например, если ток течет вертикально сверху вниз (Рис 5.), то правый буравчик нужно вращать по часовой стрелке (глядя сверху), а конец его рукоятки, находящийся в точке А, будет двигаться при этом от чертежа к читателю; так будет направлено и магнитное поле в точке B. Формулы (1) и (2), выражающие напряженность магнитного поля элемента тока, носят название закона Био-Савара-Лапласа.

Всякое вещество под действием магнитного поля приобретает магнитный момент - намагничивается. Поэтому всякое вещество является магнетиком. Намагниченное вещество создаёт свое поле , которое вместе с первичным полем образует результирующее поле:

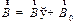
(27.1)

Для поля также как и для поля справедлива теорема Гаусса. Поэтому и результирующего поля справедлива теорема Гаусса:

.

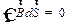(27.2)

Механизм намагничения

Молекулы многих веществ обладают собственным магнитным моментом. Каждому магнитному моменту соответствует элементарный круговой ток, создающий в окружающем пространстве магнитное поле. При отсутствии внешнего магнитного поля магнитные моменты молекул ориентированы беспорядочно, поэтому магнитное поле в среднем равно нулю.

Если вещество поместить во внешнее магнитное поле, то магнитные моменты молекул приобретают ориентацию преимущественно в одном направлении и вещество намагничивается.

Если молекулы вещества в отсутствии внешнего магнитного поля не имеют магнитных моментов, то при внесении во внешнее магнитное поле в молекулах индуцируются элементарные круговые токи (молекулярные токи) и молекулы вещества приобретают упорядоченный магнитный момент.

Большинство веществ намагничиваются слабо. Сильными магнитными свойствами обладают только ферромагнитные вещества: железо, никель, кобальт и их сплавы.

Степень намагничения магнетика характеризуется магнитным моментом единицы объёма. Эту величину называют намагниченностью и обозначают 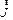. По определению

,

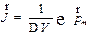(27.3)

где 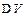– физически малый объём в окрестности данной точки, 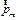–магнитный момент отдельной молекулы. Суммирование проводится по всем молекулам в объёме .

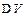Намагниченность можно определить и так:

,

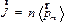(27.4)

где 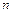- концентрация молекул, а 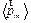- средний магнитный момент молекулы.

Токи намагничения.

Рассмотрим цилиндр из однородного магнетика, намагниченность 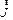которого однородна и направлена вдоль оси цилиндра. Принимая, что все молекулы обладают одинаковым магнитным моментом 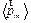, покажем на

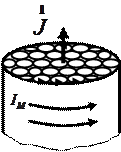
на рисунке 27.1 ориентацию молкулярных токов, изобразив их окружностями. У соседних молекул молекулярные токи в местах их соприкосновения текут в противоположных направлениях и взаимно компенсируют друг друга. Нескомпен­сированными остаются только те, которые выходят на боковую поверхность цилиндра. Эти токи и образуют макроско­пически повер­хностный ток намагни­чивания 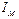,циркулирующий по боковой поверхности цилиндра.

Рисунок 27. 1.

Циркуляция вектора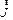

Вначале убедимся, что для стационарного случая и произвольной поверхности:

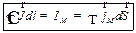
(27.5)

Для доказательства вычислим алгебраическую сумму токов охватываемых

контуром Г (см.рис. 27.2). Натянем на контур произвольную поверхность S Из рисунка 2 видно, что одни молекулярные токи пересекают поверхность дважды. Такие токи не вносят никакого вклада в результирующий ток намагни­чивания через поверхность S. Но те токи, которые обвиваются вокруг контура Г, пересекают поверхность только один раз. Такие молекулярные токи и создают макроскопический ток намагничивания 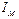, пронизы­вающий поверхность S.

Рисунок 27.2

Пусть каждый молекулярный ток равен 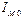, а площадь S_м. Тогда из рисунка 27.2 видно, что элемент dl контура Г обвивают те молекулярные токи, центры которых попадают внутрь косого цилиндрика с объёмом dV=S_мcosα dl. Их вклад в ток намагничивания

,

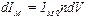(27.6)

где n - концентрация молекул. Подставив выражение для dV получим

.

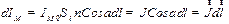(27.7)

Здесь учтено, что 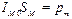– магнитный момент молекулярного тока, а 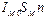– магнитный момент единицы объёма вещества. Проинтегрировав по всему контуру, получим выражение (27.). Теорема доказана.

Если магнетик неоднородный, то ток намагничивания пронизывает весь объем, а не только поверхность.

Дифференциальная форма уравнения получается с помощью теоремы Стокса:

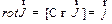
(27.8)

Магнитомеханические явления

Найдём величину магнитного момента создаваемого током электрона p_m в атоме. Пусть электрон движется со скоростью v по орбите радиуса r. Через площадку, расположенную в любом месте на пути электрона, переносится в единицу времени заряд eν, где е – заряд электрона, а ν – число оборотов в секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы 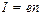. Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент равен:

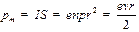
(27.9)

так как 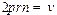– скорость электрона.

Момент обусловлен движением электрона по орбите, вследствие чего называется орбитальным магнитным моментом. Направление 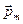образует с направлением тока правовинтовую систему, а с направлением движения электрона левовинтовую.

Движущийся по орбите электрон обладает так же моментом импульса

,

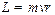(27.10)

где 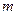– масса, 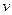- скорость электрона.

Вектор 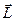называется орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему, следовательно, 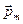и 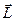противоположно направлены.

Отношение магнитного момента и механического для элементарной частицы называется магнитомеханическим ( или гиромагнитным) отношением. Для электрона оно равно

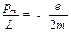
(27.11)

где знак минус указывает на то, что направления моментов противоположны.

Вследствие вращения электрона вокруг ядра атом оказывается подобным волчку. Это обстоятельство лежит в основе магнитомеханических явлений, заключающихся в том, что намагничение магнетика приводит к его вращению и, наоборот, вращение магнетика вызывает его намагничивание.

Теорема о циркуляции вектора (для магнитного поля постоянных токов).

В магнетиках, помещенных во внеш­нее магнитное поле, возникают токи намагничивания, поэтому циркуляция вектора 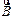теперь будет определяться не только токами проводимости, но и токами намагничивания, а именно:

,

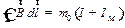(27.12

где 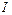и 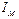— токи проводимости и намагничивания, охватываемые заданным контуром Г.

В общем случае определение токов 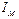задача сложная, формула () становится малопригод­ной в практическом отношении. Оказывается, однако, можно ввести некоторый вспомогательный вектор, цирку­ляция которого будет определяться только токами прово­димости, охватываемыми контуром Г. Действительно, из (ЖЖЖЖ) и (27.12) следует

.

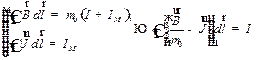(27.13)

Величину, стоящую под интегралом в скобках, обозна­чают буквой .

.

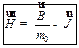(27.14)

Величину часто называют напряженностью маг­нитного поля

Итак, есть некоторый вспомогательный век­тор , циркуляция которого по произвольному контуру Г равна алгебраической сумме токов проводимости I, охватывае­мых этим контуром:

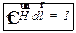
(27.15)

Эта формула выражает теорему о циркуляции вектора : циркуляция вектора по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром.

Правило знаков для токов то же, что и в случае цир­куляции вектора .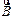

Единицей величины является ампер на метр (А/м).

Дифференциальная форма теоремы о циркуляции вектора :

,

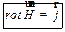(27.16)

т. е. ротор вектора равен плотности тока проводимости в той же точке вещества.

Заметим, что вектор :

1) представляет собой комбина­цию двух совершенно различных величин 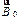и 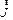. Поэто­му вектор — это вспомогательный вектор, не имеющий сколько-нибудь глубокого физического смысла;

2) за­висит, вообще говоря, от всех токов — и от токов проводимости, и от токов намагничивания

Однако важное свойство вектора , выраженное в теореме о его циркуляции, оправдывает введение этого вектора: во многих случаях он значительно упрощает изу­чение поля в магнетиках.

Дата добавления: 2015-07-02