Связь между векторами и . Магнитная восприимчивость

На­магниченность 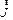принято связывать не с силовой характеристикой магнитного поля 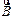, а с вектором . Рассмотрим такой магнетик, для которого зависимость между 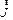и имеет линейный характер:

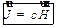
(27.17)

где 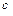— магнитная восприимчивость, без­размерная величина, характерная для каждого данного магнетика (безразмерность 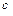следует из того, что согласно (27.14) размерности и ).

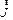Магнитная восприимчивость 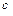бывает как положительной, так и отрицательной. Соответ­ственно магнетики, подчиняющиеся зависимости (27.17), подразделяют на парамагнетики ( 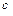> 0) и диамагнетики ( 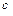< 0). У парамагнетиков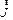 ­­ , у диамагнетиков ­¯ .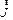

Связь между 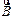и . Магнитная проницаемость.

Для магнетиков, которые подчи­няются зависимости (27.17), выражение (27.14) принимает вид 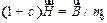. Отсюда

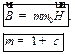
(27.18)

где 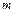- магнитная проницаемость среды.

У парамагнетиков 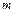> 1, у диамагнетиков 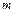<1, при­чем как у тех, так и у других 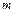, отличается от единицы весьма мало, т. е. магнитные свойства этих магнетиков вы­ражены очень слабо.

Можно показать, что вели­чина 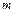показывает, во сколько раз увеличивается магнит­ная индукция 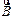при заполнении магнетиком всего про­странства, занимаемого полем.

Граничные условия для 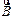и

Условие для вектора .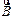

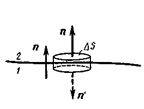
	Из теоремы Гаусса для вектора магнитной индукции 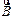следует равенство нормальных составляющих вектора магнитной индукции на границе раздела сред, т.е. 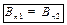. (27.19) Доказательство: см. рис.27.3.
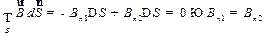
Рисунок 27.3

Дата добавления: 2015-07-02