
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условия для вектора
|
|
|
|
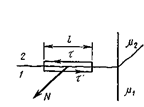
| Из теоремы о циркуляции для вектора  следует, что разность тангенциальных составляющих вектора следует, что разность тангенциальных составляющих вектора  на границе раздела сред равна поверхностной плотности тока на границе раздела сред равна поверхностной плотности тока 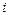 , т.е. , т.е.
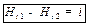 . (27.20)
Доказательство: см. рис.27.4.. . (27.20)
Доказательство: см. рис.27.4..
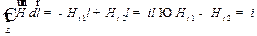
|
| Рисунок 27.4 |
Если на границе раздела магнетиков токов проводимости нет (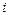 = 0), то тангенциальная составляющая вектора
= 0), то тангенциальная составляющая вектора  оказывается одинаковой по обе стороны границы раздела:
оказывается одинаковой по обе стороны границы раздела:
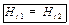
| (27.21) |
Заметим, что на границе раздела вектор 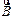 ведет себя аналогично вектору
ведет себя аналогично вектору 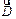 , а вектор
, а вектор  — аналогично вектору
— аналогично вектору 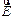 .
.
Магнитная защита. На границе раздела двух магнетиков линии вектора  испытывают преломление (рис. 27.5). На преломлении магнитных линий основана магнитная защита. При внесении, например, замкнутой железной оболочки (слоя) во внешнее магнитное поле линии этого поля будут концентрироваться (сгущаться) преимущественно в самой оболочке. Внутри
испытывают преломление (рис. 27.5). На преломлении магнитных линий основана магнитная защита. При внесении, например, замкнутой железной оболочки (слоя) во внешнее магнитное поле линии этого поля будут концентрироваться (сгущаться) преимущественно в самой оболочке. Внутри
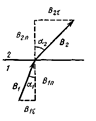
| же этой оболочки — в полости — магнитное поле оказывается сильно ослабленным по сравнению с внешним полем. Другими словами, железная оболочка обладает экранирующим действием. Это используют для предохранения чувствительных приборов от внешних магнитных полей. |
| Рисунок 27.5 |
Диамагнетизм
Электрону, вращающемуся по орбите (см. рис. 27.6), присущи все особенности поведения гироскопов под действием внешних сил. При соответствующих условиях должна возникать прецессия электронной орбиты. Условия, необходимые для прецессии, осуществляются, если атом находится во внешнем магнитном поле 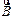 . В этом случае на орбиту действует вращательный момент
. В этом случае на орбиту действует вращательный момент
 , ,
| (27.22) |
стремящийся установить орбитальный магнитный момент электрона 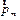 по направлению поля.
по направлению поля.
Под действием момента сил 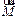 векторы
векторы 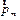 m и
m и 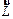 совершают прецессию вокруг направления вектора
совершают прецессию вокруг направления вектора 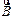 . Найдём скорость прецессии.
. Найдём скорость прецессии.
За время dt вектор 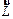 получает приращение
получает приращение 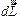 , равное
, равное
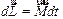 . .
| (27.23) |
Вектор 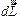 , как и вектор
, как и вектор 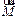 , перпендикулярен к плоскости, проходящей через векторы
, перпендикулярен к плоскости, проходящей через векторы 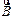 и
и 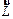 , а его модуль равен
, а его модуль равен
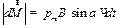 , ,
| (27.24) |
где α - угол между 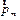 и
и 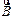 .
.
За время dt плоскость, в которой лежит вектор 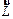 , повернётся на угол
, повернётся на угол
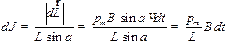 . .
| (27.25) |
Разделив этот угол на dt. Найдём угловую скорость прецессии:
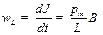 . .
| (27.26) |
Подставив в формулу гиромагнитное отношение (27.11), получим
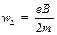
| (27.27) |
Частоту ωL – называют частотой ларморовой прецессии или просто

| ларморовой частотой. Она не зависит ни от угла наклона орбиты, ни от радиуса орбиты или скорости электрона и, следовательно, для всех электронов, входящих в состав атома, одинакова.
Прецессия орбиты обуславливает дополнительное движение электрона вокруг направления поля. Если бы расстояние r’ электрона от параллельной 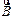 оси, проходящей через центр орбиты, не изменялось, то дополнительное движение происходило бы по окружности радиуса r’ (см. рис. 27.7.). оси, проходящей через центр орбиты, не изменялось, то дополнительное движение происходило бы по окружности радиуса r’ (см. рис. 27.7.).
|
| Рисунок 27.6 |
Этому соответствовал бы круговой ток
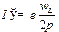 , ,
| (27.28) |
магнитный момент, которого
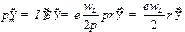 , ,
| (27.29) |
направлен в сторону, противоположную В. Этот момент называется индуцированным (наведённым) магнитным моментом.

| В действительности, вследствие движения электрона по орбите, расстояние r’ всё время меняется. Поэтому нужно брать <r’2> среднее по времени значение. Это среднее зависит от угла α, характеризующего ориентацию плоскости орбиты по отношению к 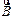 . В частности, для орбиты, перпендикулярной к вектору . В частности, для орбиты, перпендикулярной к вектору 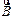 (α=0), r’ постоянно и (α=0), r’ постоянно и
|
| Рисунок 27.7 |
равно радиусу орбиты r.
Для орбиты, плоскость которой проходит через направление 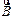 (α=π/2), r’ изменяется по закону r’=r sin ωt, где ω – угловая скорость вращения по орбите (Рис.3). Орбита лежит в плоскости рисунка.
(α=π/2), r’ изменяется по закону r’=r sin ωt, где ω – угловая скорость вращения по орбите (Рис.3). Орбита лежит в плоскости рисунка.

| Следовательно,
Если произвести усреднение по всем α, то есть учесть, что электрон вращается по всей поверхности сферы, то получим: Подставив в (27.29) значение ларморовой прецессии ωL получим для | ||
| Рисунок 27.8 |
среднего индуцированного магнитного момента одного электрона:
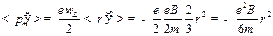
| (27.30) |
Знак минус отражает то обстоятельство, что 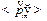 и
и 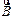 направлены в противоположные стороны.
направлены в противоположные стороны.
Просуммировав выражение по всем электронам, найдём индуцированный магнитный момент атома:
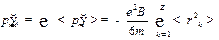 . .
| (27.31) |
Итак под действием внешнего магнитного поля происходит прецессия электронных орбит с одинаковой для всех электронов угловой скоростью. Это приводит к возникновению индуцированного магнитного момента направленного против поля. Ларморова прецессия возникает у всех без исключения веществ. Однако в тех случаях, когда атомы обладают сами по себе магнитным моментом, магнитное поле не только индуцирует момент, но и устанавливает (ориентирует) магнитный момент атома по направлению поля. Возникающий при этом положительный (направленный по полю) момент бывает значительно больше, чем отрицательный индуцированный момент. Поэтому результирующий момент оказывается положительным и вещество ведёт себя как парамагнетик.
Диамагнетизм обнаруживают только те вещества, у которых атомы не обладают магнитным моментом. Это бывает когда векторная сумма орбитальных и спиновых (собственных) моментов электронов атома равна нулю. Если для такого вещества умножить равенство (27.31) на число Авогадро NA, то получится магнитный момент моля вещества. Разделив его на напряжённость поля, найдём молярную магнитную восприимчивость χм. Магнитная проницаемость диамагнетиков практически равна единице. Таким образом,
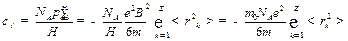 . .
| (27.32) |
Квантовая механика даёт тот же результат.
Подстановка значений даёт для χм=10-10-10-11, что хорошо согласуется с экспериментальными данными.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 821; Нарушение авторских прав?; Мы поможем в написании вашей работы!
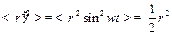 .
.
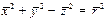 , следовательно
, следовательно 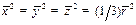 . Отсюда для вращения в плоскости орбиты будем иметь
. Отсюда для вращения в плоскости орбиты будем иметь 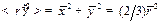 . (Здесь
. (Здесь 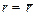 , так как он не меняется по модулю).
, так как он не меняется по модулю).