Коэффициент детерминации (D)

Парный линейный коэффициент корреляции Бравэ-Пирсона (r).

Парный линейный коэффициент корреляции Бравэ-Пирсона вычисляется в том случае, когда между показателями исследуемых выборок (Х _i и У _i) существует линейная связь.

Если Х и У независимые случайные величины, то коэффициент корреляции равен 0. Заметим, что обратное утверждение неверно. Если r = 0, то между изучаемыми признаками нет линейной корреляционной зависимости, но это условие не исключает существования какого-либо другого вида корреляционной зависимости (параболической, показательной и др.)

Одна из формул для расчета коэффициента корреляции Бравэ-Пирсона:

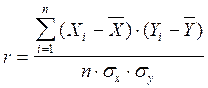
где X_i, Y_i - показатели первой и второй выборок соответственно;

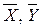- средние арифметические значения первой и второй выборок соответственно;

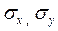- стандартные отклонения первой и второй выборок соответственно;

n - объем каждой выборки.

Абсолютная величина коэффициента корреляции не превосходит единицы: 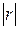< 1.

Коэффициент корреляции характеризует степень зависимости, или тесноту (силу) зависимости между Х и У, чем больше 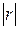, т. е. чем ближе он к 1, тем сильнее (теснее) связь между изучаемыми признаками, а чем ближе он к 0, тем слабее.

Принято считать, если:

· коэффициент корреляции равен 1, то между исследуемыми признаками наблюдается функциональная связь;

· изменяется от ±0,9 до ± 0,7 - сильная статистическая связь;

· изменяется от ±0,69 до ±0,5 - средняя статистическая связь;

· изменяется от ± 0,49 до ±0,2 - слабая статистическая связь;

· коэффициент корреляции равен нулю - то между изучаемыми признаками нет линейной корреляционной зависимости.

Таким образом, коэффициент корреляции Бравэ-Пирсона r используется только при наличии линейной взаимосвязи между исследуемыми признаками. Существует несколько видов коэффициентов корреляции: парный линейный коэффициент корреляции Бравэ - Пирсона r, ранговый коэффициент корреляции Спирмэна r, тетрахорический коэффициент сопряженности Т, коэффициент множественной корреляции r _xyz, коэффициент частной корреляции r _xyz.

После вычисления любого из перечисленных выше коэффициентов корреляции, необходимо рассчитать его достоверность с использованием критерия Стьюдента.

В некоторых случаях тесноту связи случайных величин характеризуют коэффициентом детерминации D, равным:

.

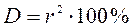Коэффициент детерминации показывает, какой процент взаимосвязи результатов двух выборок объясняется их взаимовлиянием.

Остальная часть (100 - D)% объясняется влиянием других неучтённых факторов.

Дата добавления: 2015-07-02