
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная регрессия
|
|
|
|
РЕГРЕССИОННЫЙ АНАЛИЗ
При изучении корреляционной связи было отмечено, что коэффициент корреляции показывает степень связи, направление связи, форму связи между двумя исследуемыми выборками, но он не дает возможности определить, как количественно меняется одна величина по мере изменения другой.
Регрессия - это зависимость среднего значения случайной величины У от величины Х и, наоборот, зависимость среднего значения случайной величины Х от величины У, описанная уравнением, полученная путем построения эмпирической или теоретической линии регрессии и с помощью вычисления коэффициентов регрессии. Существует линейная и нелинейная взаимосвязь между исследуемыми показателями, следовательно, можно составить уравнение линейной или нелинейной регрессии.
Существует зависимость между двумя показателями и несколькими. И уравнения регрессии могут быть множественными.
В выборе регрессионной модели помогает графическое представление экспериментальных данных в виде диаграммы рассеяния или корреляционного поля. По выборочным данным составляется корреляционное поле, на которое наносятся также средние значения У в каждом интервале изменения Х. Эти точки соединяются между собой ломаной линией, по виду которой можно судить, как в среднем меняется У в зависимости от изменения Х. Такая ломаная линия называется эмпирической линией регрессии. Затем ломаную линию аппроксимируют прямой линией. При линейной зависимости можно сделать проще: заменить корреляционный эллипс прямой линией.
Линейная регрессия, или линейная форма связи между случайными переменными занимает особое место в теории корреляции. При такой форме связи У есть линейная функция от Х, т. е.
У = а + b×Х,
где а и b – коэффициенты регрессии, Х – независимая случайная переменная. Линейная регрессия обусловливается двумерным нормальным законом распределения пары случайных величин (Х, У).
Параметры в уравнении регрессии, т. е. коэффициенты регрессии, определяются по способу наименьших квадратов. Суть его заключается в том, чтобы сумма квадратов отклонений измеренных величин от истинного значения была бы минимальной.
В случае линейной регрессии за теоретическое значение принимается значение У, получаемое по известной формуле, т. е. ищется такая прямая линия, сумма квадратов отклонений измеренных Уi от которой была бы минимальной.
Значения коэффициентов регрессии определяются решением системы нормальных уравнений.
Расчёт коэффициентов уравнений линейной регрессии
Как уже было сказано выше, в случае линейной зависимости уравнение регрессии является уравнением прямой линии.
Различают
У = ау/х +bу/х×Х - прямое уравнение регрессии;
Х = ах/у+bх/у ×Y - обратное уравнение регрессии.
Здесь а и b – коэффициенты, или параметры, которые определяются по формулам. Значение коэффициента b вычисляется
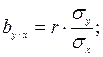
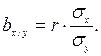
Из формул видно, что коэффициенты регрессии bу/х и bх/у имеют тот же знак, что и коэффициент корреляции, размерность, равную отношению размерностей изучаемых показателей Х и У, и связаны соотношением:
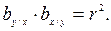
Для вычисления коэффициента а достаточно подставить в уравнения регрессии средние значения коррелируемых переменных

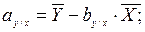
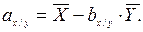
График теоретических линий регрессии (рис. 17) имеет вид:

Рис 17. Теоретические линии регрессии
Из приведённых выше формул легко доказать, что угловые коэффициенты прямых регрессии равны соответственно
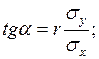
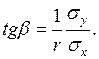
Так как 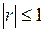 , то
, то 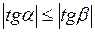 . Это означает, что прямая регрессии Y на Х имеет меньший наклон к оси абсцисс, чем прямая регрессии Х на Y.
. Это означает, что прямая регрессии Y на Х имеет меньший наклон к оси абсцисс, чем прямая регрессии Х на Y.
Чем ближе 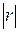 к единице, тем меньше угол между прямыми регрессии. Эти прямые сливаются только тогда, когда
к единице, тем меньше угол между прямыми регрессии. Эти прямые сливаются только тогда, когда 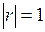 .
.
При 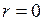 прямые регрессии описываются уравнениями
прямые регрессии описываются уравнениями 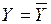 ,
, 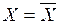 .
.
Таким образом, уравнения регрессии позволяют:
· определить, насколько изменяется одна величина относительно другой;
· прогнозировать результаты.
2. Методика выполнения расчётно-графической работы №2
Расчётно-графическая работа содержит 4 раздела.
В первом разделе:
3. Формулируется тема;
4. Формулируется цель работы.
Во втором разделе:
3. Формулируется условие задачи;
4. Заполняется таблица исходных данных выборки.
В третьем разделе:
4. Результаты измерений представляются в виде вариационного ряда;
5. Даётся графическое представление вариационного ряда.
6. Формулируется вывод.
В четвёртом разделе:
3. Рассчитываются основные статистические характеристики ряда измерений;
4. По итогам расчётов формулируется вывод.
Оформление работы:
3. Работа выполняется в отдельной тетради или на форматных листах.
4. Титульный лист заполняется по образцу.
Российский Государственный Университет
физической культуры, спорта, молодёжи и туризма
Кафедра естественнонаучных дисциплин
Корреляционный и регрессионный анализы
Расчётно-графическая работа №2
по курсу математики
Выполнил: студент 1 к. 1 пот. 1гр.
Иванов С.М.
Преподаватель:
доц. кафедры ЕНД и ИТ
(Ф.И.О.)
Москва – 2012
(Пример оформления титульного листа)
Пример выполнения расчётно-графической работы №2.
Тема работы: Корреляционный и регрессионный анализы.
Цель работы: Определить взаимосвязь показателей двух выборок.
Ход выполнения работы:
1. Придумать две выборки из своего вида спорта с одинаковым объемом n.
2. Нарисовать корреляционное поле, сделать предварительный вывод.
3. Рассчитать коэффициент корреляции Бравэ-Пирсона и сделать вывод.
4. Определить достоверность коэффициента корреляции и сделать окончательный вывод.
5. Рассчитать коэффициент детерминации и сделать вывод о степени взаимосвязи показателей двух выборок.
6. Рассчитать коэффициенты прямого и обратного уравнений регрессии.
7. Построить теоретические линии регрессии на корреляционном поле и показать точку их пересечения.
1. Условие задачи: У группы спортсменов определяли результаты в беге на 100 м с барьерами Xi (с) и прыжках в длину Yi (м) (табл.). Проверить, существует ли корреляционная связь между исследуемыми признаками и определить достоверность коэффициента корреляции.
Таблица исходных данных выборки: Результаты приведены в таблице исходных данных.
Таблица 6
Результаты бега и прыжка
| № п/п | |||||||||
| Xi, с | 13,68 | 13,34 | 13,75 | 13,51 | 13,53 | 13,7 | 13,45 | 13,72 | 13,61 |
| Yi, м | 6,35 | 6,83 | 6,25 | 6,38 | 6,42 | 6,35 | 6,51 | 6,06 | 6,22 |
| № п/п | |||||||||
| Xi, с | 13,84 | 13,91 | 13,46 | 13,5 | 13,6 | 13,35 | 13,42 | 13,8 | 13,5 |
| Yi, м | 6,20 | 6,00 | 6,50 | 6,65 | 6,55 | 6,75 | 6,60 | 6,18 | 6,55 |
Решение:
2. Построим корреляционное поле (диаграмму рассеяния) и сделаем предварительный вывод относительно связи между исследуемыми признаками.
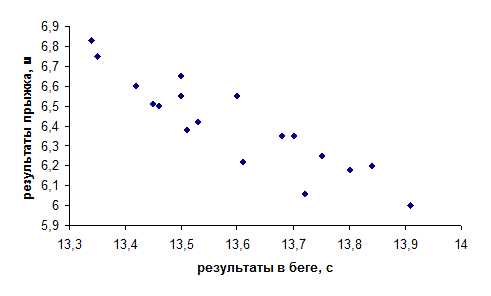
Рис 18. Корреляционное поле
Предварительный вывод:
Связь между показателями результатов в беге на 100 м с барьерами Xi (с) и прыжками в длину Yi (см):
· линейная;
· отрицательная;
· сильная.
3. Рассчитаем парный линейный коэффициент корреляции Бравэ – Пирсона, предварительно рассчитав основные статистические показатели двух выборок. Для их расчёта составим таблицу, в которой предпоследний и последний столбцы необходимы для расчёта стандартных отклонений, если они неизвестны. Для нашего примера эти значения рассчитаны в первой расчётно-графической работе, но для наглядности покажем расчёт дополнительно.
Таблица 7
Вспомогательная таблица для расчета коэффициента
корреляции Бравэ – Пирсона
| № | Xi, с | Yi, см | 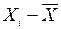
| 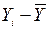
| 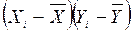
| 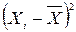
| 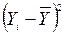
|
| 13,68 | 6,35 | 0,09 | -0,06 | -0,005 | 0,0081 | 0,0036 | |
| 13,34 | 6,83 | -0,25 | 0,42 | -0,105 | 0,0625 | 0,18 | |
| 13,75 | 6,25 | 0,16 | -0,16 | -0,03 | 0,0256 | 0,0256 | |
| 13,51 | 6,38 | -0,08 | -0,03 | 0,0024 | 0,0064 | 0,0009 | |
| 13,53 | 6,42 | -0,06 | 0,01 | -0,0006 | 0,0036 | 0,0001 | |
| 13,7 | 6,35 | 0,11 | -0,06 | -0,0066 | 0,0121 | 0,0036 | |
| 13,45 | 6,51 | -0,14 | 0,1 | -0,014 | 0,0196 | 0,01 | |
| 13,72 | 6,06 | 0,13 | -0,35 | -0,0455 | 0,0169 | 0,1225 | |
| 13,61 | 6,22 | 0,02 | -0,19 | -0,004 | 0,0004 | 0,0361 | |
| 13,84 | 6,20 | 0,25 | -0,21 | -0,0525 | 0,0625 | 0,0441 | |
| 13,91 | 6,00 | 0,32 | -0,41 | -0,1312 | 0,1024 | 0,1681 | |
| 13,46 | 6,50 | -0,13 | 0,09 | -0,0117 | 0,0169 | 0,0081 | |
| 13,5 | 6,65 | -0,09 | 0,24 | -0,0216 | 0,0081 | 0,0576 | |
| 13,6 | 6,55 | 0,01 | 0,14 | 0,0014 | 0,0001 | 0,0196 | |
| 13,35 | 6,75 | -0,24 | 0,34 | -0,0816 | 0,0576 | 0,1156 | |
| 13,42 | 6,60 | -0,17 | 0,19 | -0,0323 | 0,0289 | 0,0361 | |
| 13,8 | 6,18 | 0,21 | -0,23 | -0,0483 | 0,0441 | 0,0529 | |
| 13,5 | 6,55 | -0,09 | 0,14 | -0,0126 | 0,0081 | 0,0196 | |
| n= 18 | 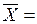 13,59 13,59
| 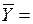 6,41
6,41
| ∑=-0,6015 | ∑=0,4839 | ∑=0,9041 |
sx = 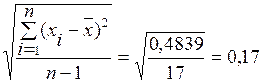 ,
,
sy = 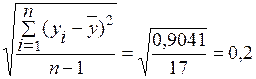 ,
,
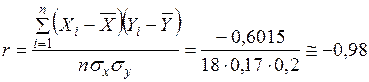 .
.
Полученное значение коэффициента корреляции позволяет подтвердить предварительный вывод и сделать окончательное заключение – связь между исследуемыми признаками:
· линейная;
· отрицательная;
· сильная.
4. Определим достоверность коэффициента корреляции.
Предположим, что связь между результатом в беге на 100 м и прыжком в длину отсутствует (Но: r= 0).
· 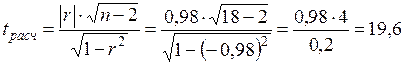 .
.
· Находим 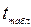 = 2,12 для α = 0,05 и n = n - 2 = 16.
= 2,12 для α = 0,05 и n = n - 2 = 16.
· tрасчет > tтабл (19,6 > 2,12).
Вывод: существует сильная, отрицательная статистически достоверная (р =0,95) связь между бегом с препятствиями на дистанцию 100 м и прыжком в длину. Это означает, что с улучшением результата в прыжке в длину уменьшается время пробега дистанции 100 м.
5. Вычислим коэффициент детерминации:
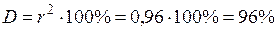 .
.
Следовательно, только 96% взаимосвязи результатов в беге на 100 м с барьерами и в прыжке в длину объясняется их взаимовлиянием, а остальная часть, т. е. 4% объясняется влиянием других неучтённых факторов.
6. Рассчитаем коэффициенты прямого и обратного уравнений регрессии, воспользовавшись формулами, подставим значения рассчитанных коэффициентов в соответствующую формулу и запишем прямое и обратное уравнения регрессии:
Y = а1 + b1×Х - прямое уравнение регрессии;
Х = а2 + b2 ×Y - обратное уравнение регрессии.
Воспользуемся результатами расчёта, приведёнными выше:
sx = 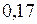 ; sy =
; sy = 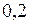 ;
; 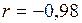 ;
; 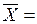 13,59;
13,59; 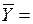 6,4,
6,4,
Рассчитаем коэффициент b1, воспользовавшись формулой:
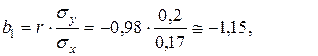
Для расчета коэффициента а1 подставим в прямое уравнение регрессии вместо b1 рассчитанное значение, а вместо Х и Y средние арифметические значения двух выборок из таблицы:
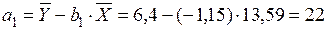
Подставим полученные значения коэффициентов а1 и b1 в прямое уравнение регрессии и запишем уравнение прямой линии:
Y = 22 - 1,15 ×Х
Рассчитаем коэффициент b2, воспользовавшись формулой:
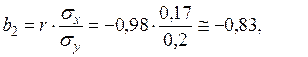
Для расчета коэффициента а2 подставим в прямое уравнение регрессии вместо b2 рассчитанное значение, а вместо Х и Y средние арифметические значения двух выборок из таблицы:
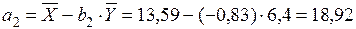
Подставим полученные значения коэффициентов а1 и b1 в прямое уравнение регрессии и запишем уравнение прямой линии:
Х = 18,92 - 0,83 ×Y
Таким образом, мы получили прямое и обратное уравнения регрессии:
Y = 22 - 1,15 ×Х - прямое уравнение регрессии;
Х = 18,92 - 0,83 ×Y - обратное уравнение регрессии.
Для проверки правильности расчётов достаточно подставить в прямое уравнение среднее значение 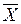 и определить значение Y. Полученное значение Y должно быть близким или равным среднему значению
и определить значение Y. Полученное значение Y должно быть близким или равным среднему значению 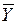 .
.
Y = 22 - 1,15 × 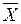 = 22 - 1,15 × 13,59 = 6,4 =
= 22 - 1,15 × 13,59 = 6,4 = 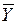 .
.
При подстановке в обратное уравнение регрессии среднего значения 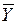 , полученное значение Х должно быть близким или равным среднему значению
, полученное значение Х должно быть близким или равным среднему значению 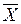 .
.
Х = 18,92 - 0,83 × 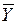 = 18,92 - 0,83 × 6,4 = 13,6 =
= 18,92 - 0,83 × 6,4 = 13,6 = 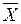 .
.
7. Построим линии регрессии на корреляционном поле.
Для графического построения теоретических линий регрессии, как и для построения любой прямой, необходимо иметь две точки из диапазона значений Х и Y.
Причём, в прямом уравнении регрессии независимая переменная Х, а зависимая Y, а в обратном – независимая переменная Y, а зависимая Х.
Y = 22 - 1,15 ×Х
| X | 13,42 | 13,8 |
| Y | 6,57 | 6,13 |
Х = 18,92 - 0,83 ×Y
| Y | 6,2 | 6,6 |
| X | 13,77 | 13,44 |
Координатами точки пересечения линий прямого и обратного уравнений регрессии являются значения средних арифметических двух выборок (с учётом погрешностей округлений при приближённых расчётах).
Вывод: зная результат бега с препятствиями на дистанцию 100 м, по прямому уравнению регрессии, можно теоретически определить результат прыжка в длину; и наоборот, зная результат прыжка в длину по обратному уравнению регрессии, можно определить результат бега с препятствиями.
ПРИЛОЖЕНИЕ
| Таблица 1 | |||||
| Критические значения t -критерия Стьюдента | |||||
| Число степеней свободы ν | Уровень значимости a для двусторонней критической области | ||||
| 0,1 | 0,05 | 0,01 | 0,005 | 0,001 | |
| ¥ | 2,9200 2,1318 1,9432 1,8595 1,8125 1,7823 1,7613 1,7459 1,7341 1,7247 1,7171 1,7109 1,7056 1,7011 1,6973 1,6939 1,6909 1,6883 1,6860 1,6839 1,6759 1,6706 1,6669 1,6641 1,6620 1,6602 1,6588 1,6576 1,6449 | 4,3027 2,7765 2,4469 2,3060 2,2281 2,1788 2,1448 2,1199 2,1009 2,0860 2,0739 2,0639 2,0555 2,0484 2,0423 2,0369 2,0322 2,0281 2,0244 2,0211 2,0086 2,0003 1,9944 1,9901 1,9867 1,9840 1,9818 1,9799 1,9600 | 9,9250 4,6041 3,7074 3,3554 3,1693 3,0545 2,9768 2,9208 2,8784 2,8453 2,8188 2,7970 2,7787 2,7633 2,7500 2,7385 2,7284 2,7195 2,7116 2,7045 2,6778 2,6603 2,6479 2,6387 2,6316 2,6259 2,6213 2,6174 2,5758 | 14,0892 5,5975 4,3168 3,8325 3,5814 3,4284 3,3257 3,2520 3,1966 3,1534 3,1188 3,0905 3,0669 3,0470 3,0298 3,0149 3,0020 2,9905 2,9803 2,9712 2,9370 2,9146 2,8987 2,8870 2,8779 2,8707 2,8648 2,8599 2,8070 | 31,5998 8,6101 5,9587 5,0414 4,5868 4,3178 4,1403 4,0149 3,9217 3,8496 3,7922 3,7454 3,7067 3,6739 3,6460 3,6218 3,6007 3,5821 3,5657 3,5510 3,4960 3,4602 3,4350 3,4164 3,4019 3,3905 3,3811 3,3734 3,2905 |
| Число степеней свободы ν | 0,05 | 0,025 | 0,005 | 0,0025 | 0,0005 |
| Уровень значимости a для односторонней критической области |
| Таблица 2 | ||||||||||||||||||
| Критические значения F -критерия Фишера-Снедекора (ν1 - число степеней свободы большей дисперсии; ν2 - число степеней свободы меньшей дисперсии) | ||||||||||||||||||
| Уровень значимости a = 0,05 | ||||||||||||||||||
| ν2 | ν1 | |||||||||||||||||
| 6,39 5,19 4,53 4,12 3,84 3,63 3,48 3,36 3,26 3,11 3,01 2,87 2,78 2,69 2,61 2,56 2,50 2,46 | 6,26 5,05 4,39 3,97 3,69 3,48 3,33 3,20 3,11 2,96 2,85 2,71 2,62 2,53 2,45 2,40 2,35 2,30 | 6,16 4,95 4,28 3,87 3,58 3,37 3,22 3,09 3,00 2,85 2,74 2,60 2,51 2,42 2,34 2,29 2,23 2,19 | 6,09 4,88 4,21 3,79 3,50 3,29 3,14 3,01 2,92 2,77 2,66 2,52 2,43 2,34 2,25 2,20 2,14 2,10 | 6,04 4,82 4,15 3,73 3,44 3,23 3,07 2,95 2,85 2,70 2,59 2,45 2,36 2,27 2,18 2,13 2,07 2,03 | 6,00 4,78 4,10 3,68 3,39 3,18 3,02 2,90 2,80 2,65 2,54 2,40 2,30 2,21 2,12 2,07 2,01 1,97 | 5,96 4,74 4,06 3,63 3,34 3,13 2,97 2,86 2,76 2,60 2,49 2,35 2,26 2,16 2,07 2,02 1,97 1,92 | 5,93 4,70 4,03 3,60 3,31 3,10 2,94 2,82 2,72 2,56 2,45 2,31 2,22 2,12 2,04 1,98 1,93 1,88 | 5,91 4,68 4,00 3,57 3,28 3,07 2,91 2,79 2,69 2,53 2,42 2,28 2,18 2,09 2,00 1,95 1,89 1,85 | 5,87 4,64 3,96 3,52 3,23 3,02 2,86 2,74 2,64 2,48 2,37 2,23 2,13 2,04 1,95 1,90 1,84 1,79 | 5,84 4,60 3,92 3,49 3,20 2,98 2,82 2,70 2,60 2,44 2,33 2,18 2,09 1,99 1,90 1,85 1,79 1,75 | 5,80 4,56 3,87 3,44 3,15 2,93 2,77 2,65 2,54 2,39 2,28 2,12 2,02 1,93 1,84 1,78 1,72 1,68 | 5,74 4,50 3,81 3,38 3,08 2,86 2,70 2,57 2,46 2,31 2,20 2,04 1,94 1,84 1,74 1,69 1,62 1,57 | 5,71 4,46 3,77 3,34 3,05 2,82 2,67 2,53 2,42 2,27 2,16 1,99 1,89 1,79 1,69 1,63 1,56 1,51 | 5,70 4,44 3,75 3,32 3,03 2,80 2,64 2,50 2,40 2,24 2,13 1,96 1,86 1,76 1,66 1,60 1,53 1,48 | 5,68 4,42 3,72 3,29 3,00 2,77 2,61 2,47 2,36 2,21 2,09 1,92 1,82 1,72 1,61 1,55 1,47 1,42 | 5,66 4,40 3,71 3,28 2,98 2,76 2,59 2,45 2,35 2,19 2,07 1,90 1,80 1,69 1,59 1,52 1,45 1,39 | ||
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 4316; Нарушение авторских прав?; Мы поможем в написании вашей работы!