Виды статистических гипотез

Статистические гипотезы

Гипотеза - научное предположение.

Статистическая гипотеза - предположение о характеристиках, которые доказываются методами математической статистики. Статистическую гипотезу обычно обозначают буквой Н (от греческого Hipotes).

Гипотеза называется нулевой (Но), если отсутствует различие между сравниваемыми выборками ().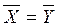

Противоположной (альтернативной или единичной) гипотезой (Н₁) будет предположение о том, что .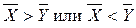

· Гипотеза о доверительном интервале.

· Гипотеза о достоверности различий средних арифметических:

-связанных выборок;

-несвязанных выборок.

· Гипотеза о достоверности различий дисперсий.

· Гипотеза о достоверности коэффициента корреляции.

При проверке статистических гипотез решение никогда не принимается с уверенностью, т.е. всегда есть вероятность принять неправильное решение.

Уровень значимости - вероятность появления ошибки при выборе гипотезы.

Следует отметить, что любая гипотеза должна формулироваться, а уровень значимости 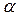задаётся исследователем всегда до получения экспериментальных данных, по которым эта гипотеза будет проверяться.

В таблице приведены значения вероятности события при различных значениях ошибки предположения.

Уровень значимости и вероятность события

Таблица 5

Вероятность ошибки уровень значимости (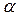)	Вероятность события (р) %	Доверительная вероятность q =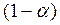
полная уверенность	100 %
0,05 (5 %)	95 %	0,95
0,01 (1 %)	99 %	0,99
0,001 (0,1 %)	99,9 %	0,999

Уровень значимости 0,05 означает, что ошибочное значение может встретиться, например, в 5 наблюдениях из 100.

Обычно в научных исследованиях в области физической культуры и спорта считается достаточной доверительная вероятность 0,95 (95%), тогда уровень значимости 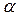составляет 0,05 (5%).

Только в тех случаях, когда выводы, сделанные в конкретном исследовании, связаны с большой ответственностью или же уточняются результаты предыдущих исследований, применяются высокие уровни доверительной вероятности: 99 или 99,9% (уровень значимости 0,01 (1 %) или 0,001 (0,1 %) соответственно).

Доверительная вероятность – вероятность, признанная достаточной для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик.

Основные этапы проверки статистической гипотезы.

1. Формулировка гипотезы, которую в дальнейшем необходимо принять или отклонить.

Но: 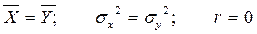(r-коэффициент корреляции)

H₁:

2. Определить расчетное значение критерия, то есть некоторой

величины по определенной заданной формуле.

Критерий – правило, с помощью которого подтверждается или отвергается та или иная гипотеза.

tрасч.	Fpacч.	tpacч. r (коэффициента корреляции)
критерий Стьюдента	критерий Фишера	критерий Стьюдента

3. Определить табличные критические значения (по таблице, см. приложение).

tтабл., Fтабл.

Для этого необходимо знать:

n - число степеней свободы и - уровень значимости.

4. Сравнить значения расчетного коэффициента с табличным:

tpacч.ó tтабл. Fpacч. ó Fтабл.

5. Сделать вывод. Статистическая гипотеза принимается или отвергается.

а) если tpacч. £ tтабл. (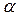,n), то нулевая гипотеза о том, что средние значения двух выборок равны (Но: ) принимается с вероятностью q =1- ;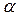

если tpacч.> tтабл. - нулевая гипотеза отвергается, тем самым утверждается, что средние арифметические двух выборок не равны.

б) если Fрасч.<Fтабл., то нулевая гипотеза о равенстве дисперсий двух выборок (Но: 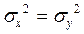) принимается с вероятностью q =1- , то есть дисперсии не различаются и выборки однородны;

если Fpacч ³ Fтабл., то нулевая гипотеза отклоняется с вероятностью q =1- , указывая на то, что показатели двух выборок имеют существенные отклонения от среднего значения и выборки неоднородны. (). Из двух выборок более однородна будет та, у которой значение дисперсии меньше.

Дата добавления: 2015-07-02