
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинетическая энергия твердого тела 1 страница
|
|
|
|
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис.21).

| Мысленно разобьем это тело на маленькие объемы с элементарными массами 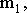  находящимися на расстоянии находящимися на расстоянии 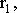  от оси вращения. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri с различными линейными скоростями от оси вращения. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri с различными линейными скоростями 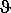
|
Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
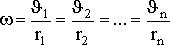 (4.2)
(4.2)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
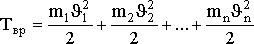 или
или 
Используя выражение (4.2), получим
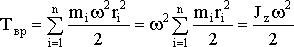
где Jz -момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела pавна
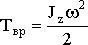 (4.3)
(4.3)
Из сравнения формулы (4.3) с выражением (3.4) для кинетической
энергии тела, движущегося поступательно  следует, что момент инерции вращательного движения - мера инертности тела. Формула (4.3) справедлива для тела, вращающегося вокруг неподвижной оси. В случае цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии вращения и энергии поступательного движения.
следует, что момент инерции вращательного движения - мера инертности тела. Формула (4.3) справедлива для тела, вращающегося вокруг неподвижной оси. В случае цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии вращения и энергии поступательного движения.
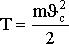
где m - масса скатывающегося тела; vс - скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через центр его масс; w - угловая скорость тела
Гироскопы
Гироско́п(от др.-греч. γυρο «вращение» и др.-греч. σκοπεω «смотреть») — устройство, способное измерять изменение углов ориентации связанного с ним тела относительно инерциальной системы координат.
Схема простейшего механического гироскопа в карданном подвесе
Основные типы гироскопов по количеству степеней свободы:
2-степенные,
3-степенные.
Основные два типа гироскопов по принципу действия:
механические гироскопы,
оптические гироскопы.
По режиму действия гироскопы делятся на:
датчики угловой скорости,
указатели направления.
Однако одно и то же устройство может работать в разных режимах в зависимости от типа управления.
Среди механических гироскопов выделяется ро́торный гироско́п — быстро вращающееся твёрдое тело, ось вращения которого способна изменять ориентацию в пространстве. При этом скорость вращения гироскопа значительно превышает скорость поворота оси его вращения. Основное свойство такого гироскопа — способность сохранять в пространстве неизменное направление оси вращения при отсутствии воздействия на неё моментов внешних сил.
Впервые это свойство использовал Фуко в 1852 г. для экспериментальной демонстрации вращения Земли. Именно благодаря этой демонстрации гироскоп и получил своё название от греческих слов «вращение», «наблюдаю».
Свойства роторного гироскопа
При воздействии по оси чувствительности момента внешней силы, стремящейся изменить направленность в пространстве оси собственного вращения, эта ось гироскопа начинает отклоняться не по оси действия момента, а по перпендикулярной ей. В результате гироскоп вращается вокруг измерительной оси, перпендикулярной направлению вектора приложенного момента (явление прецессии).
Данное свойство напрямую связано с возникновением так называемой кориолисовой силы. Так, при воздействии момента внешней силы гироскоп поначалу будет вращаться именно в направлении действия внешнего момента (нутационный бросок). Каждая частица гироскопа будет таким образом двигаться с переносной угловой скоростью вращения из-за момента. Но роторный гироскоп, помимо этого, и сам вращается, значит, каждая частица будет иметь относительную скорость. Следовательно, возникнет кориолисова сила, которая будет заставлять гироскоп двигаться в перпендикулярном приложенному моменту направлению, то есть прецессировать. Прецессия вызовет кориолисову силу, момент которой скомпенсирует момент внешней силы.
Гироскопический эффект вращающихся тел есть проявление коренного свойства материи — её инертности.
Упрощённо, поведение гироскопа описывается уравнением:
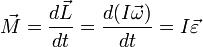
где векторы 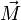 и
и  являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр
являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр  — его моментом инерции, векторы
— его моментом инерции, векторы  и
и  угловой скоростью и угловым ускорением.
угловой скоростью и угловым ускорением.
Свойства гироскопа используются в приборах — гироскопах, основной частью которых является быстро вращающийся ротор, который имеет несколько степеней свободы (осей возможного вращения).
Чаще всего используются гироскопы, размещённые в карданном (кардановом) подвесе (см. рис.). Такие гироскопы имеют 3 степени свободы, то есть он может совершать 3 независимых поворота вокруг осей АA', BB' и CC', пересекающихся в центре подвеса О, который остаётся по отношению к основанию A неподвижным.
Гироскопы, у которых центр масс совпадает с центром подвеса O, называются астатическими, в противном случае — тяжёлыми гироскопами.
Для обеспечения вращения ротора гироскопа с высокой скоростью применяются специальные гиромоторы.
Для управления гироскопом и снятия с него информации используются датчики угла и датчики момента.
Гироскопы используются в виде компонентов как в системах навигации (авиагоризонт, гирокомпас, ИНС и т. п.), так и в нереактивных системах ориентации и стабилизации космических аппаратов.
принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.
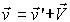
Равенство (5) называют законом сложения скоростей Галилея. Ясно, что это векторное равенство эквивалентно трем равенствам (подобным (3)) для соответствующих компонент скоростей.
Аналогично, дифференцируя равенство (5) по времени:

и вспоминая, что 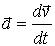
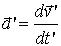
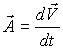 , получим закон преобразования ускорения тела (в системе К, в К’) при переходе из одной системы отсчета в другую:
, получим закон преобразования ускорения тела (в системе К, в К’) при переходе из одной системы отсчета в другую:
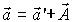
II закон Ньютона
Второй закон Ньютона. произведение массы тела на ускорение равно действующей на это тело силе, создающей это ускорение. Векторы силы и ускорения ВСЕГДА имеют одинаковые направления.
Второй закон Ньютона справедлив только в инерциальных системах.
Ускорение, сообщаемое телу в результате одновременного действия нескольких сил, равно ускорению, которое сообщает ему их равнодействующая
Сила инерции,
векторная величина, численно равная произведению массы т материальной точки на ее ускорение w и направленная противоположно ускорению. При криволинейном движении С. и. можно разложить на касательную, или тангенциальную составляющую Jt направленную противоположно касательному ускорению wt, и на нормальную, или центробежную составляющую Jn, направленную вдоль главной нормали к траектории от центра кривизны; численно Jt = nwt, Jn = mv2/r, где v — скорость точки, r — радиус кривизны траектории. При изучении движения по отношению к инерциальной системе отсчёта С. и. вводят для того, чтобы иметь формальную возможность составлять уравнения динамики в форме более простых уравнений статики.
Понятие о С. и. вводится также при изучении относительного движения. В этом случае присоединение к действующим на материальную точку силам взаимодействия с другими телами переносной Jпер и Кориолиса Jкop С. и. позволяет составлять уравнения движения этой точки в подвижной (неинерциальной) системе отсчёта так же, как и в инерциальной
Принцип относительности. Любые физические явления при одних и тех же условиях протекают одинаково во всех инерциальных системах отсчёта.
Постулат о постоянстве скорости света. Во всех инерциальных системах отсчёта скорость света в вакууме является предельной и не зависит от скорости движения источника и наблюдателя.
Релятивистская кинематика. При движении с релятивистской, то есть близкой к скорости света c, скоростью υ длина отрезка сокращается:

l0 - интервал времени в покоящейся системе отсчёта, β = υ/c.
При движении с релятивистской скоростью интервалы времени увеличиваются:
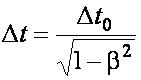
Δt0 - интервал времени в покоящейся системе отсчёта.
Релятивистская динамика. При движении с релятивистской скоростью υ масса растёт:
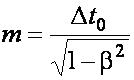
m0 - масса покоя тела.
Релятивистская кинетическая энергия:
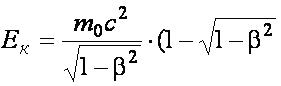
Связь массы и энергии:

Масса и энергия - две взаимосвязанные характеристики любого физического объекта. Энергия покоя (собственная энергия) тела равна
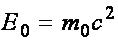
В основе специальной теории относительности А. Эйнштейна лежат два постулата, смысл которых можно выразить так:
1. При одинаковых условиях, реализованных по отдельности в двух системах отсчета - некоторой инерциальной системы К и системы К', движущейся равномерно и прямолинейно относительно системы I - любые физические процессы в этих системах отсчета протекают одинаково.
2. В природе существует предельная (максимальная) скорость распространения физических сигналов (взаимодействий), одна и та же во всех инерциальных системах отсчета. Эта максимальная скорость совпадает со скоростью света в вакууме, она не зависит от движения источника и приемника света и равна с = 300000 км/с.
Из первого принципа следует: если для данной задачи (некоторого класса задач) найдена инерциальная система отсчета I, то для этой задачи существует и бесчисленное множество инерциальных систем типа II, движущихся равномерно прямолинейно относительно I. Скорости всех систем II меньше с. Системы отсчета необходимо связывать с телами, а скорости тел не могут равняться или превосходить максимальную скорость света в вакууме, равную с. Скорости тел строго меньше максимальной.
Развитие науки показало, что оба принципа Эйнштейна подтверждаются всей совокупностью экспериментальных и теоретических знаний современной физики.
Из принципов Эйнштейна следует: одновременность разноместных событий не является абсолютной, независимой от систем отсчета.
Действительно, пусть от лампы L, находящейся на середине платформы, движущейся со скоростью V, начал распространяться свет.
Преобразования Лоренца - соотношения, позволяющие переходить /в теории относительности/:
- от пространственно-временных координат некоторого события в одной инерциальной системе отсчета;
- к пространственно-временным координатам этого же события в другой инерциальной системе отсчета.
Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.
Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.
Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.
С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.
Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.
Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразованияй Лоренца под c следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся - в своих рамках - от их применения в фундаментальной физике).
Если ИСО K' движется относительно ИСО K с постоянной скоростью V вдоль оси x, а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:
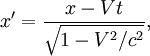
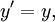
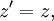
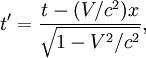
где c — скорость света в вакууме, величины со штрихами измерены в системе K', без штрихов — в K.
ДЕФОРМАЦИЯ ТЕЛА – изменение формы или размеров тела. Деформация может возникать в результате механического воздействия, теплового расширения, действия электрических и магнитных полей и др.
Деформация называется упругой, если она полностью исчезает после прекращения действия вызвавших ее внешних сил, и пластической, если она не исчезает после прекращения действия этих сил.
Механические колебания
Многообразные движения тел в окружающем нас мире можно разделить на два класса в зависимости от того, остается ли тело в процессе движения вблизи некоторого среднего положения или такого положения нет. Мы обратимся к первому классу. Отличительной чертой многих движений рассматриваемого класса является их периодичность, т. е. повторяемость через определенные интервалы времени.
Движения, которые точно или приблизительно повторяются через одинаковые промежутки времени, называются механическими колебаниями.
Колебания бывают разные. Одни колебания, как, например, в швейной машине, способны совершаться только тогда, когда на тело действуют периодически изменяющиеся внешние силы, которые и вынуждают тело совершать колебательное движение. Такие колебания называют вынужденными. Другие же колебания обусловлены действием внутренних сил и потому способны происходить сами по себе. Таковы, например, колебания грузика на пружине, возникающие после того, как грузик сместили из положения равновесия и отпустили.
Колебания, происходящие под действием внутренних сил и возникающие в системе после того, как система была выведена из состояния равновесия и предоставлена самой себе, называются свободными.
К свободным колебаниям относятся: колебания груза на пружине, а также груза на нити (маятника).
Отличительной особенностью систем, в которых происходят свободные колебания, является наличие у них положения устойчивого равновесия. Именно около этих положений и совершаются свободные колебания.
Для того чтобы в той или иной системе возникли свободные колебания, необходимо выполнение следующих условий:
1. Системе должна быть сообщена избыточная энергия. Эту энергию можно сообщить системе либо в виде потенциальной энергии, либо в виде кинетической энергии, либо в виде и той и другой.
2. Избыточная энергия, сообщенная системе, не должна в процессе возникшего движения полностью тратиться на преодоление трения.
Эти два условия являются необходимыми, но не достаточными для существования свободных колебаний. Система, помимо этого, должна обладать еще некоторыми определенными свойствами, которые могут послужить причиной возникновения в системе колебаний.
Основные кинематические характеристики колебаний:
1) амплитуда колебаний (А)— это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда свободных колебаний определяется начальными условиями, измеряется амплитуда в метрах;
2) период колебания (Т)— это минимальный промежуток времени, по истечении которого система возвращается в прежнее состояние; иначе говоря, период колебания — это время, за которое совершается одно полное колебание;
3) частота колебаний (υ)— это число колебаний, совершаемых за 1 с, измеряется в герцах (Гц);
4) циклическая частота (w)— это величина, в 2π раз большая частоты.

Физический смысл циклической частоты заключается в том, что она показывает, какое число колебаний совершается за 2π секунд. Измеряется циклическая частота в, или с-1.
Для периода, частоты и циклической частоты справедлива формулы:
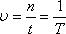

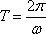
где п — число колебаний, а t — время, за которое произошло п колебаний.
В процессе свободных колебаний положение колеблющегося тела непрерывно изменяется. Если трение настолько мало, что им можно пренебречь, то графиком зависимости координаты колеблющегося тела (материальной точки) от времени является синусоидальная кривая, или, кратко, синусоида.
График зависимости координаты колеблющегося тела от времени называют графиком колебаний. По графику колебаний легко определяются все кинематические характеристики колебательного движения.
Колебания, при которых координата колеблющегося тела меняется с течением времени по закону синуса (или косинуса), называются гармоническими.
Если момент начала отсчета времени колебаний совпадает с моментом максимального отклонения маятника от положения равновесия, уравнение колебаний будет:
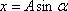


Вынужденные колебания. Резонанс.
Колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями. Внешняя периодическая сила, называемая вынуждающей, сообщает колебательной системе дополнительную энергию, которая идет на восполнение энергетических потерь, происходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или косинуса, то вынужденные колебания будут гармоническими и незатухающими.
В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной.
Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ0, происходит резкое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при υ = υ0 внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний Ат от частоты вынуждающей силы υ представлен на рисунке, этот график называется резонансной кривой:
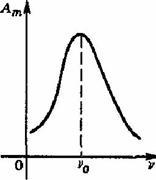
Явление резонанса играет большую роль в ряде природных, научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.
Упругие волны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.
В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны.
В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны.В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям.
Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами.
Упругие волны в твёрдых телах
Наиболее распространёнными типами упругих волн в твёрдых телах являются:
продольные волны
поперечные волны, движение частиц перпендикулярно направлению распространения волны
поверхностные волны (например волны Рэлея, где движение частиц происходит по эллипсам)
волны в тонких пластинах — нормальные волны (волны Лэмба)
Практическое применение
Упругие волны широко используются:
В медицине
ультразвуковое исследование
В технике
акустические методы нерузрушающего контроля
ультразвуковая диагностика
ультразвуковая толщинометрия
В музыке
Камертон
Орган
Звук – колебательное движение частиц упругой среды, распространяющееся в виде волн (колебания плотности, давления).
Не может распространяться в вакууме! Продольная волна в жидкостях и газах!
| Инфразвуки (до 16 Гц) | Слышимые звуки (16 – 20000Гц) | Ультразвуки (более 20000 Гц) | Гиперзвуки (109 – 1013 Гц) | |
| Источники | Шум атмосферы, леса, моря. Гром. Взрывы, орудийные выстрелы. Сейсмические волны. | Колебания твердого тела (мембраны, деки, диффузоры громкоговорителей). Колебания ограниченных объемов среды (воздух в музыкальных духовых инструментах, органах, свистках). Голосовой аппарат человека и животных. | Пьезоэлектрические материалы. Магнитострикционные материалы. Некоторые животные (дельфины, летучие мыши и др.). | Тепловое движение атомов. Пьезоэлектрические и магнитострикционные материалы. |
| Применение | Определение места взрыва, выстрела. Предсказание цунами. Исследование атмосферы. | Ориентация в пространстве. Общение, речь, получение информации. | Дефектоскопия, медицина, эхолокация. Физика твердого тела. Получение эмульсий. Ускорение диффузии, некоторых химических реакций. Ориентация в пространстве у некоторых животных. | Изучение состояния вещества. Линии задержки (цветное телевидение, ЭВМ и т.п.) |
Характеристики звука.
1. Спектр – разложение на гармонические колебания по частотам. Восприятие звука органами слуха зависит от того, какие частоты входят в состав звуковой волны. Шум - звуки, образующие набор частот, непрерывно заполняющих некоторый интервал (сплошной спектр частот). Музыкальные (тональные) звуки – звуки, образующие линейчатый спектр частот: частоты n входящие в состав музыкальных звуков, образуют ряд дискретных значений. Музыкальным звукам соответствуют периодические или почти периодические колебания. Каждая синусоидальная звуковая волна называется тоном.
Высота тона зависит от частоты: чем больше частота, тем выше тон. Основным тоном сложного музыкального звука называется тон, соответствующий наименьшей частоте, которая имеется в наборе частот данного звука. Тоны, соответствующие остальным частотам в составе звука, называются обертонами. Если частоты обертонов кратны частоте основного тона, то обертоны называются гармоническими, причем основной тон с частотой n0 называется первой гармоникой, обертон со следующей частотой 2n0 - второй гармоникой и т. д.
Музыкальные звуки с одним и тем же основным тоном различаются тембром, который определяется наличием обертонов - их частотами и амплитудами, характером нарастания амплитуд в начале звучания и их спадом в конце звучания.
2. Звуковое давление – давление, оказываемое звуковой волной на препятствие.
3.Интенсивность звуковой волны – энергия, переносимая звуковой волной через единицу поверхности за единицу времени().
4. Громкость звука зависит от интенсивности звука, т. е. определяется амплитудой колебаний в звуковой волне. Наибольшей чувствительностью органы слуха обладают к звукам с частотами от 700 до 6000 Гц. В этом диапазоне ухо способно воспринимать звуки с интенсивностью около 10-12-10-11 Вт/м2.
Порогом слышимости называется наименьшая интенсивность звуковой волны, которая может быть воспринята органами слуха. Стандартный порог слышимости принимается равным I0=10-12 Вт/м2 при частоте n=1 кГц.
Порогом болевого ощущения называется наибольшая интенсивность звуковой волны, при которой восприятие звука не вызывает болевого ощущения. Порог болевого ощущения зависит от частоты звука (на частоте 1 кГц равен 1 Вт/м2).
Мерой чувствительности органов слуха к восприятию звуковых волн данной интенсивности является уровень интенсивности (громкости):. Единица измерения – децибел
Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он даже не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, тот услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Для волн, распространяющихся в какой-либо среде (например, звука) нужно принимать во внимание движение как источника так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, имеет значение только[1] относительное движение источника и приёмника.
Эффект был впервые описан Кристианом Доплером в 1842 году.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 471; Нарушение авторских прав?; Мы поможем в написании вашей работы!