Кинетическая энергия твердого тела 2 страница

Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью. В этом случае в лабораторной системе регистрируется черенковское излучение, имеющее непосредственное отношение к эффекту Доплера.

Сущность явления

Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется — длина волны увеличивается.

где f0 — частота, с которой источник испускает волны, c — скорость распространения волн в среде, v — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).

Частота, регистрируемая неподвижным приёмником

Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника.

u — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).

Подставив значение частоты из формулы (1) в формулу (2), получим формулу для общего случая.

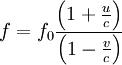
Сейсмические волны,

колебания, распространяющиеся в Земле от очагов землетрясений, взрывов и других источников. Вблизи очагов сильных землетрясений С. в. обладают разрушительной силой при доминирующем периоде в десятые доли сек. На значительных расстояниях от эпицентров С. в. являются упругими волнами.

Продольные С. в. (Р) переносят изменения объёма в среде — сжатия и растяжения. Колебания в них совершаются в направлении распространения (рис. 1, а). Поперечные С. в. (S) не образуют в среде объёмных изменений и представляют собой колебания частиц, происходящие перпендикулярно направлениям распространения волны (рис. 1, б). В каждый момент и в каждой точке среды сейсмические колебания удовлетворяют (для Р и S волн) волновым уравнениям. В однородной изотропной упругой среде скорости распространения продольных (а) и поперечных (в) волн определяются формулам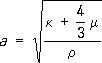и:

и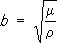

Здесь 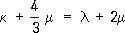k — модуль всестороннего сжатия; l и m — константы Ляме, причём m называется модулем сдвига. Скорость продольных волн больше поперечных.

Особенность распространения С. в. (упругих волн в твёрдой среде) состоит в том, что при косом падении на поверхность раздела сред с различными параметрами (скоростями и плотностями) волны одного типа, например продольной, возникают, кроме отражённой и преломленной продольных волн (рис. 2), волны отраженные и преломленные поперечные. Вблизи поверхностей раздела в Земле возникают поверхностные С. в. При распространении неоднородной волны SH вдоль горизонтального слоя возникает волна Лява. В случае падения на граничную плоскость волны Р в слое могут возникать отражённые волны Р и SV. При этом, если а2 > в2 > а1 > в1, где a1 и в1 — скорости в слое, a a2 и в2 — в неприлежащей среде, то как отражённая Р, так и отражённая SV при малом e1 обладают свойством полного внутреннего отражения. В результате в слое формируются волны Рэлея. Они, как и волны Лява, обладают дисперсией скоростей. Волны Рэлея возникают в полупространстве без слоистости. Тогда они не диспергируют и их скорость с " 0,9 в.

Волны Р и S распространяются из источника по объёму Земли. Они называются объёмными. Их амплитуда для однородной и изотропной среды убывает обратно пропорционально расстоянию. Поверхностные волны, распространяясь вдоль поверхности, обладают амплитудой, убывающей обратно пропорционально корню квадратному из расстояния. По этой причине в колебаниях от удалённых землетрясений по амплитуде доминируют поверхностные волны.

Благодаря изменениям свойств Земли с глубиной изменяются и скорости распространения объёмных С. в. Это приводит к их рефракции в недрах Земли.

Наблюдения на поверхности Земли над распространением С. в. позволяют исследовать строение Земли. Зависимость скорости распространения волн Р и S от глубины (рис. 3) позволила выявить ряд оболочек "твёрдой" Земли. Подробности строения Земли см. в ст. Земля.

Деформа́ция (от лат. deformatio — искажение) — изменение относительного положения частиц тела, связанное с их перемещением. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое напряжение.

Деформации разделяют на упругие и пластические. Упругие деформации исчезают[1], а пластические остаются после окончания действия приложенных сил. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

Способность веществ пластически деформироваться называется пластичностью. При пластическом деформировании металла одновременно с изменением формы меняется ряд свойств, в частности, при холодном деформировании повышается прочность.

Изучение деформации

Деформация тела вполне определяется, если известен вектор перемещения каждой его точки. Деформация твёрдых тел в связи со структурными особенностями последних изучается физикой твёрдого тела, а движения и напряжения в деформируемых твёрдых телах — теорией упругости и пластичности. У жидкостей и газов, частицы которых легкоподвижны, исследование деформации заменяется изучением мгновенного распределения скоростей.

Причины возникновения деформации твёрдых тел

Деформация твёрдого тела может явиться следствием фазовых превращений, связанных с изменением объёма, теплового расширения, намагничивания (магнитострикционный эффект), появления электрического заряда (пьезоэлектрический эффект) или же результатом действия внешних сил.

Упругая и пластическая деформация

Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки, и пластической, если после снятия нагрузки она не исчезает (во всяком случае полностью). Все реальные твёрдые тела при деформации в большей или меньшей мере обладают пластическими свойствами. При некоторых условиях пластическими свойствами тел можно пренебречь, как это и делается в теории упругости. Твёрдое тело с достаточной точностью можно считать упругим, то есть не обнаруживающим заметных пластических деформаций, пока нагрузка не превысит некоторого предела.

Природа пластической деформации может быть различной в зависимости от температуры, продолжительности действия нагрузки или скорости деформации. При неизменной приложенной к телу нагрузке деформация изменяется со временем; это явление называется ползучестью. С возрастанием температуры скорость ползучести увеличивается. Частными случаями ползучести являются релаксация и последействие упругое. Одной из теорий, объясняющих механизм пластической деформации, является теория дислокаций в кристаллах.

Сплошность

В теории упругости и пластичности тела рассматриваются как "сплошные". Сплошность, то есть способность заполнять весь объём, занимаемый материалом тела без всяких пустот является одним из основных свойств, приписываемых реальным телам. Понятие сплошности относится также к элементарным объёмам, на которые можно мысленно разбить тело. Изменение расстояния между центрами каждых двух смежных бесконечно малых объёмов у тела, не испытывающего разрывов, должно быть малым по сравнению с исходной величиной этого расстояния.

Простейшая элементарная деформация

Простейшей элементарной деформацией является относительное удлинение некоторого элемента:

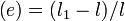
где

l1 — длина элемента после деформации;

l — первоначальная длина этого элемента.

На практике чаще встречаются малые деформации, так что e << 1.

Измерение деформации

Причины отказа механики

Прогиб

Коррозия

Пластическая деформация

Усталость материала

Трещина

Плавление

Износ

Измерение деформации производится либо в процессе испытания материалов с целью определения их механических свойств, либо при исследовании сооружения в натуре или на моделях для суждения о величинах напряжений. Упругие деформации весьма малы, и измерение их требует высокой точности. Наиболее распространённый метод исследования деформации — с помощью тензометров. Кроме того, широко применяются тензодатчики сопротивления, поляризационно-оптический метод исследования напряжения, рентгеновский структурный анализ. Для суждения о местных пластических деформациях применяют накатку на поверхности изделия сетки, покрытие поверхности легко растрескивающимся лаком и т. д.

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

Для тонкого растяжимого стержня закон Гука имеет вид: 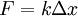Здесь F сила натяжения стержня,x — его удлинение, а k называется коэффициентом упругости (или жёсткостью).

Очевидно, что коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Полезно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как 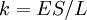Величина E называется модулем Юнга и зависит только от свойств материала. Полезно теперь ввести относительное удлинение и нормальное напряжение в поперечном сечении 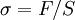. В этих обозначениях закон Гука записывается как 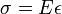. Величину, обратную жёсткости, называют гибкостью.

Следует иметь ввиду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т.е. найдем упругую энергию растянутой пружины.

Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила, с которой действует пружина, не остается постоянной при изменении растяжения. Мы видели (§ 37), что сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.

Значит, среднее значение силы равно Fср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы:

A=1/2 kl•l=1/2kl2.

Таким образом, потенциальная энергия упругости Еп равна

Eп = 1/2 kl2. (98.1)

Здесь потенциальная энергия выражена через коэффициент упругости пружины и через наибольшее растяжение ее. Полученное выражение для потенциальной энергии можно записать и иначе, через величину силы упругости при наибольшем растяжении и коэффициент упругости:

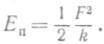
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т. е. чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы, т. е. работа.

Это имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, погашая вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы будут меньше и конструкция самолета будет лучше предохранена от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке.

Хрупкость (свойство, противоположное пластичности) – способность материала разрушаться без заметной пластической деформации.

Пластичность - способность материала получать остаточные деформации без разрушения и сохранять их после снятия нагрузки;

Изучению движения и механического равновесия жидкостей и газов и их взаимодействию между собой и с твёрдыми телами посвящён раздел механики — гидроаэромеханика (часто называется также гидродинамикой). Гидроаэромеханика — часть более общей отрасли механики, механики сплошной среды.

Гидромеханика — это раздел гидроаэромеханики, в котором рассматриваются несжимаемые жидкости. Поскольку сжимаемость жидкостей очень мала, во многих случаях ей можно пренебречь. Изучению сжимаемых жидкостей и газов посвящена газовая динамика.

Гидромеханика подразделяется на гидростатику, в которой изучают равновесие несжимаемых жидкостей, и гидродинамику (в узком смысле), в которой изучают их движение.

Движение электропроводных и магнитных жидкостей изучается в магнитной гидродинамике. Для решения прикладных задач применяется гидравлика.

Основной закон гидростатики - закон Паскаля.

Движение идеальной несжимаемой жидкости описывается уравнением Эйлера. Для стационарного потока такой жидкости выполняется закон Бернулли. Вытекание жидкости из отверстий описывается формулой Торичелли.

Движение вязкой жидкости описывается уравнением Навье-Стокса, в котором возможен и учёт сжимаемости.

Упругие колебания и волны в жидкости (и в других средах) исследуются в акустике. Гидроакустика - раздел акустики, в котором изучается звук в реальной водной среде для целей подводной локации, связи и др.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

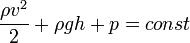
Здесь

ρ — плотность жидкости,

v — скорость потока,

h — высота, на которой находится рассматриваемый элемент жидкости,

p — давление.

Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.

Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли. (Не путать с дифференциальным уравнением Бернулли.)

Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид: .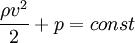

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности ρ: .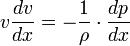

Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового (ρgh), статического (p) и динамического (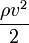) давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров, водо- и пароструйных насосов.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела всегда в точности равна нулю.

Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: пуаз, Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести.

Прибор для измерения вязкости называется вискозиметром.

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

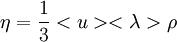где < u > — средняя скорость теплового движения молекул, λ − средняя длина свободного пробега.

Вторая вязкость

Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.

Вязкость жидкостей

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Общий закон внутреннего трения — закон Ньютона: Коэффициент вязкости η может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: η = Cew / kT

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества VM. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение 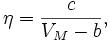где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Ньютоновские и неньютоновские жидкости

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

Сила вязкого трения

Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.

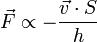
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что при наличии любой сколь угодно малой силы тела придут в движение, то есть не существует трения покоя. Это отличает вязкое трение от сухого.

Ламина́рное тече́ние (лат. lamina — пластинка, полоска) — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений) скорости и давления.

Течение жидкостей и газа

Ползучее течение

Ламинарное течение

Потенциальное течение

Отрыв течения

Вихрь

Неустойчивость

Турбулентность

Конвекция

Ударная волна

Сверхзвуковое течение

Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе .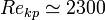

До 1917 года в российской науке пользовались термином Струйчатое течение.

Только в ламинарном режиме возможно получение точных решений уравнения движения жидкости (уравнений Навье-Стокса), например течение Пуазейля. В некоторых случаях для получения порогового числа Рейнольдса достаточно провести линейный анализ устойчивости — теоретический анализ устойчивости под воздействием бесконечно малых возмущений. Так, например, получены пороги для течения между параллельными плоскостями и течения Тейлора между вращающимися цилиндрами. Однако в некоторых случаях линейного анализа недостаточно: для течения в круглой трубе он приводит к абсолютной уТурбуле́нтность, турбуле́нция (лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключается в том, что при превышении некоторого критического числа Рейнольдса и/или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды) самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности.

Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой воды в трубах.

В гражданской авиации вхождение в зону высокой турбулентности называют воздушной ямой.

Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.

Для возникновения турбулентности необходима сплошная среда, которая подчиняется кинетическому уравнению Больцмана или Навье-Стокса или пограничного слоя. Уравнение Навье-Стокса (в него входит и уравнение сохранения массы или уравнение неразрывности) описывает множество турбулентных течений с достаточной для практики точностью.

В частном случае, она наблюдается во многих потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозэ и Ферми жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.

Она возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности.

Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.

Турбулентность, например, можно создать:

увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды) и/или число Релея (нагреть среду) и/или увеличить число Прандтля (уменьшить вязкость).

и/или задать очень сложный вид внешней силы (например, сделать ее хаотичной, например удар). Течение может не иметь фрактальных свойств.

и/или создать сложные граничные и/или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.

и/или создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии.

облучить среду звуком высокой интенсивности.

с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.стойчивости, что опровергается экспериментами.

Число Рейно́льдса — безразмерное соотношение, которое, как принято считать, определяет ламинарный или турбулентный режим течения жидкости или газа. Число Рейнольдса также считается критерием подобия потоков.

Число Рейнольдса определяется следующим соотношением: 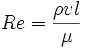, где ρ — плотность среды, v — характерная скорость, l — характерный размер, μ — динамическая вязкость среды.

Переход от ламинарного к турбулентному режиму происходит по достижении так называемого критического числа Рейнольдса Rekp. При Re < Rekp течение происходит в ламинарном режиме, при Re > Rekp возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе .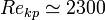

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение.

Критерий назван в честь выдающегося английского физика О. Рейнольдса (1842—1912), автора многочисленных пионерских работ по гидродинамике.

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с законом Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Создавшаяся разница давлений и порождает подъёмную силу. Полная аэродинамическая сила — это интеграл от давления вокруг контура крыла.

где:

L — это подъёмная сила,

D — это тяга,

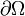- граница профиля,

p — величина давления,

n — нормаль к профилю

Согласно теореме Жуковского, величина подъёмной силы пропорциональна плотности среды, скорости потока и циркуляции скорости потока.

Коэффициент подъёмной силы

Коэффициент подъёмной силы - безразмерная величина, харатеризующая подъемную силу крыла определённого профиля при известном угле атаки. Коэффицинт определяется экспериментальным путём в аэродинамической трубе, либо по теореме Жуковского. Формулу расчёта подъёмной силы через коэффицент разработали братья Райт и Джон Смитон в начале 20-го века. Формула имеет вид[1]:

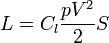
где:

L - подъёмная сила (Н)

Cl - коэффициент подъёмной силы

p - плотность воздуха (кг/м^3)

V - скорость движения крыла относительно воздуха (м/с)

S - площадь крыла (м^2)

Лобовое сопротивление — это сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивления складывается из двух типов сил: сил касательного трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности.

Силы сопротивления удобно разделить на три категории: паразитное сопротивление, индуктивное сопротивление и волновое сопротивление. Каждый тип характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Дата добавления: 2015-07-02