Сведения об инфляции 1 страница

Реальная процентная ставка — это процентная ставка, которая при отсутствии инфляции обеспечивает кредитору такую же доходность, т. е. ВНД, от займа, что и номинальная процентная ставка при наличии инфляции.

Реальная процентная ставка используется при анализе динамики процентных ставок и для приближенного пересчета платежей по займам при оценке эффективности проектов в фиксированных ценах.

Если проценты по займу начисляются постнумерандо на оставшуюся сумму долга, то связь между номинальной и реальной процентными ставками дается формулой (И. Фишера):

, (П1.3)

или в симметричном виде:

, (П1.4)

где (все показатели выражаются в долях единицы):

· p нш— номинальная процентная ставка за один шаг начисления процентов;

· p 0ш— реальная процентная ставка за один шаг начисления процентов;

· j ш— темп инфляции (темп прироста цен), средний за шаг начисления процентов;

· J ш— индекс инфляции за тот же шаг. В случае валютного займа J ши j ш заменяются, соответственно, на индекс и темп 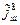валютной инфляции за шаг расчета. Для внутреннего валютного займа , где 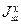— индекс роста валютного курса за шаг расчета; для внешнего (иностранного) займа — внешнему валютному индексу инфляции за шаг расчета[50].

В некоторых случаях инфляцию пытаются учесть, выполняя расчеты эффективности в фиксированных ценах, одновременно заменяя номинальную процентную ставку по займам на реальную. Использовать такой метод расчета не рекомендуется, поскольку:

1) в условиях инфляции изменяется (как правило — возрастает) потребность в заемных средствах, что не может быть учтено никакой схемой, не зависящей от конкретного проекта;

2) искажается размер налогооблагаемой прибыли и налога на прибыль. Это связано с тем, что при замене номинальной ставки на реальную изменяется соотношение между размерами погашения основного долга (которые не влияют на налогооблагаемую прибыль) и выплачиваемыми процентами (которые уменьшают налогооблагаемую прибыль).

На этом основании рекомендуется рассчитывать денежные потоки проекта, как правило, в прогнозных ценах.

На основании формул (П1.3) и (П1.4) ясно, что основное влияние на заемный капитал оказывает не сама инфляция, а ее изменение во времени. Наиболее невыгодным для проекта случаем является тот, при котором заем берется при высоком уровне инфляции и, следовательно, под высокий номинальный процент, а затем инфляция резко идет на убыль, и реальный процент, выплачиваемый заемщиком кредитору, — при той же номинальной ставке процента, — повышается.

Такая же проблема “в зеркальном отображении” стоит перед кредитором. Если он объявит слишком высокую номинальную процентную ставку, у него могут возникнуть трудности, в частности, с размещением займов; если же номинальная процентная ставка будет установлена слишком низкой, в случае увеличения темпа инфляции реальная процентная ставка может оказаться недостаточной для кредитора.

Таких проблем, связанных с весьма вероятными расхождениями фактических и прогнозных темпов инфляции, можно избежать, если при заключении кредитного соглашения устанавливать не номинальную (p _нш), а реальную (p _0ш) кредитную ставку. При этом проценты должны уплачиваться по номинальной ставке, рассчитанной в соответствии с фактической инфляцией по формуле (П1.4).

В ряде случаев бывает необходимо определить, какой заем, рублевый или валютный, выгоднее брать для финансирования проекта. Точный ответ на этот вопрос требует построения и последующего сравнения полных денежных потоков с учетом всех поступлений и выплат для каждого из займов. Однако в первом приближении можно составить мнение об относительной выгодности займов, сравнивая реальные рублевые процентные ставки по ним, выраженные в одной и той же валюте: выгоднее (в первом приближении!) тот заем, по которому эта ставка ниже.

Такое сравнение можно провести с использованием формул, имеющихся в Приложении 8. Однако в «двухвалютном приближении» (одной из валют считаются рубли, другой — «иностранная» валюта — конкретная или обобщенная) оно проводится на основе следующих рассуждений. Допустим, что для финансирования проекта предполагается использовать заем в размере А единиц иностранной валюты, предоставляемый на 1 шаг по номинальной ставке p_{н $} (чтобы не перегружать формул обозначениями, нижний индекс «ш» опущен). Принимается, что заемные средства конвертируются в рубли, а получаемые от проекта доходы частично конвертируются в валюту и направляются на погашение займа. Это значит, что заемщик получает сумму Аχ 0рублей и должен вернуть кредитору на следующем шаге сумму А (1+ p_{н $}) единиц иностранной валюты или А (1+ p_{н $}) χ 1рублей, где χ 0и χ 1— обменные курсы иностранной валюты в момент получения и погашения займа. Такая операция эквивалентна получению рублевого займа в размере Аχ 0по некоторой номинальной ставке p_{н р}, определяемой из соотношения:

. (П1.5)

Соответствующую реальную рублевую ставку p _0р можно рассчитать, используя формулу Фишера. В результате получаем:

. (П1.6)

Формулы (П1.5) и (П1.6) выражают условия эквивалентности рублевых и валютных процентных ставок.

Таким образом, при выполнении условия эквивалентности (П1.5) в первом приближении безразлично, какой брать внутренний заем, рублевый или валютный. На практике условие эквивалентности соблюдается не всегда. При этом, если реальная процентная ставка по рублевому займу больше, чем p _0р, то заемщику выгоднее получить валютный, а не рублевый заем. В противоположном случае рублевый заем оказывается выгоднее[51].

Дальнейшие выводы оказываются различными для случаев внутреннего и внешнего заимствований.

В случае внутреннего валютного займа , откуда .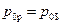

В случае внешнего валютного займа 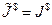, и из (П1.6) следует соотношение:

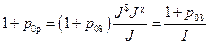, (П1.7)

где I — индекс внутренней инфляции иностранной валюты (см. раздел 8.2 основного текста)

Из (П1.7) вытекает, в частности, что сдерживание роста валютного курса относительно российской инфляции приводит к уменьшению реальной процентной ставки в рублевом выражении по валютному займу. При снижении валютного курса или низких темпах его роста реальная рублевая ставка p _0р может стать даже отрицательной, что, естественно, облегчает погашение и обслуживание долга по валютному займу.

Пример 4. Пусть длительность шага равна 1 месяцу, темп инфляции составляет 3% в месяц (j =0,03), номинальная процентная ставка — 10 % в месяц. Тогда реальная месячная процентная ставка составит . ■

Пример 5. В 1995 г. годовой темп инфляции составлял j год=200%, а ставка рефинансирования Центробанка была p год=120% годовых. Если подставить эти значения в (П1.3), получится, что реальная ставка рефинансирования была отрицательной: 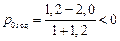. Это означает, что в указанный период ЦБ РФ финансировал коммерческие банки с убытком для себя. Между тем, такой вывод и приведенный расчет ошибочны!

Дело в том, что ЦБ РФ при выдаче займа предусматривал ежемесячное начисление процентов по ставке (10%). Среднемесячный темп инфляции можно оценить, используя формулу (8.5): . Теперь можно применить формулу (П1.3) для определения реальной среднемесячной ставки рефинансирования: . При этом реальная годовая ставка оказывается положительной: p _0год=12´ p _0мес=12´0,377%=4,52%.

Этот пример показывает, что при использовании формулы И. Фишера процентная ставка и темп инфляции относились к шагу начисления процентов. ■

Пример 6. Для осуществления российского проекта (затраты и выручка — в рублях) берется валютный заем в долларах под номинальную ставку 13% в год с начислением и выплатой процентов ежеквартально. Темп рублевой инфляции 10% в год. Прогнозируется падение обменного курса доллара на 2% в год. Найдем реальную рублевую годовую процентную ставку по этому займу, считая, что темпы инфляции и повышения валютного курса в течение года сохраняются неизменными.

Поскольку проценты начисляются и выплачиваются ежеквартально, найдем вначале все величины, относящиеся к одному кварталу (1/4 года). Номинальная процентная ставка (по правилам, принятым большинством банков) здесь будет равна 13/4=3,25%. Квартальный индекс рублевой инфляции составит J =(1+0,1)0,25=1,02411 (темп инфляции — 2,411% за квартал). Квартальный индекс изменения обменного курса J^χ =(1-0,02)0,25=0,995 (темп изменения обменного курса — -0,5% за квартал).

Теперь рассчитаем реальную рублевую квартальную процентную ставку по формуле (П1.5):

.

В пересчете на год реальная рублевая процентная ставка по валютному кредиту составит: p _0р=0,3152%´4»1,26%. Именно такой реальной процентной ставке по рублевому кредиту эквивалентна ставка валютного кредита. Заметим, что такой же при выполнении условия эквивалентности окажется и реальная валютная ставка при внутреннем займе n.

Пример 7. Полученный в предыдущем примере результат не зависел от того, каким (внутренним или внешним) являлся заем. Однако в этом примере фиксировалась номинальная валютная ставка. В то же время доходность займа для кредитора в большой степени определяется его реальной процентной ставкой. Предположим, что при тех же условиях инфляции и изменения валютного курса, что и в примере 6, берется внешний заем. Пусть годовой темп внешней инфляции равен 3%. Тогда индекс внешней инфляции за квартал составит и индекс внутенней инфляции иностранной валюты (опять-таки за квартал) окажется равным . Если допустить, что иностранный кредитор удовлетворится реальной процентной ставкой 2% за квартал (это — достаточно высокая процентная ставка— ср. с примером 6), реальная рублевая процентная ставка составит . В годовом исчислении это составит -0,66%. Таким образом, при данных условиях реальная рублевая процентная ставка окажется отрицательной. ■

Эффективная процентная ставка pef характеризует доход кредитора за счет капитализации процентов, выплачиваемых в течение периода, для которого объявлена номинальная процентная ставка. Так, если номинальная процентная ставка за год равна p н(в долях единицы), а выплата процентов по условию займа происходит m раз в год, то практически всегда банк определяет процент при каждой выплате, равный p н/ m. В этом случае эффективная годовая процентная ставка pef (в долях единицы) определяется по формуле:

. (П1.8)

Пример 8. Пусть номинальная (объявленная кредитором) годовая процентная ставка равна p =1,2 (120%), а проценты начисляются и выплачиваются ежемесячно (число выплат в год равно m =12). Тогда эффективная процентная ставка составит

. ■

П1.3. Ставка дисконта и учет систематического риска

Ставка дисконта обычно понимается как максимальная доходность альтернативных и доступных для инвестора направлений вложений (примерно то же определение дано и в основном тексте Рекомендаций). Обычно в качестве альтернативных направлений вложений принимаются вложения в инструменты финансового рынка (прежде всего — в акции). Для таких вложений доходность определяется стандартным методом (доходность акции за период рассчитывается как отношение суммы выплаченных за период дивидендов и прироста курсовой стоимости к курсовой стоимости акции на начало периода).

Однако в условиях неопределенности такая трактовка “не подходит”, поскольку высокодоходные вложения нередко связаны с высоким риском. Поэтому здесь ставку дисконта трактуют как максимальную доходность альтернативных и доступных для инвестора направлений вложений с тем же риском, что и у данного проекта. Отсюда вытекает представление ставки дисконта в виде суммы “безрисковой”, одинаковой для всех инвесторов и всех проектов (отражающей доходность вложений в безрисковые финансовые инструменты) и так называемой “премии за риск” (Risk Premium, RP), специфической для оцениваемого проекта. Обосновывается это тем, что рискованные будущие доходы являются для инвестора менее ценными по сравнению с такими же по величине безрисковыми доходами, и при определении ЧДД они должны войти в общую сумму с меньшим коэффициентом.

Ниже рассматриваются и обсуждаются два наиболее распространенных метода установления учета риска в ставке дисконта, используемых и в России при оценке имущества и инвестиционных проектов, и приводятся более корректные рекомендации.

1. Кумулятивный (пофакторный) метод. Общая идея метода состоит в следующем. Отбирается определенная группа факторов, влияющих на возможность неблагоприятных последствий реализации проекта (другими словами, понятие риска здесь согласуется с принятым в настоящих Рекомендациях). По каждому фактору указывается интервал (например, от 0% до 5%), в пределах которого, в зависимости от оценки этого фактора, оценщик выбирает размер “премии” за соответствующий риск. После этого общая “премия за риск” рассчитывается как сумма всех частных “премий”.

Разные варианты этого метода отличаются составом учитываемых факторов. Так, в одном из вариантов учитываются следующие факторы:

· необходимость проведения НИОКР с заранее неизвестными результатами;

· новизна применяемой техники или технологии, неопределенность процесса ее освоения в производстве;

· неопределенность объемов спроса и уровня цен на производимую продукцию;

· неблагоприятная для реализации проекта окружающая среда.

В другом варианте учитываются некоторые макроэкономические параметры, положение в соответствующем секторе экономики, кредитная история предприятия, профессиональные качества его менеджмента, разнообразие видов выпускаемой продукции, широта (диверсификация) потребителей продукции, степень прогнозируемости доходов и расходов предприятия и т.п.

Основные недостатки данного метода сводятся к следующему:

· одни и те же риски недопустимо учитывать одновременно и в самих денежных потоках и в ставке дисконта. Поэтому, если в ставке дисконта учтен какой-то вид рисков, денежные потоки должны быть рассчитаны при условии, что таких рисков нет. Нередко сделать это невозможно или затруднительно. Так, если часть высших менеджеров компании недостаточно квалифицирована, то денежные потоки надо было бы рассчитать применительно к ситуации, когда они будет заменены более квалифицированными менеджерами; если компания является мелкой, то потоки надо было бы рассчитать в предположении, что проект реализуется крупной компанией и т.д.;

· премии за отдельные виды рисков устанавливаются экспертно и получаемый результат отражает субъективное отношение к риску не инвестора, а аналитика (или разработчика проекта);

· предполагается, что все факторы являются независимыми и в смысле риска дополняют друг друга. Однако избежать повторного счета рисков удается не всегда. Например, поправку на риск, связанный с необходимостью проведения НИОКР, едва ли следует складывать с поправкой, соответствующей неопределенности применяемой техники или технологии, т.к. такая поправка включает и риск, связанный с необходимостью проведения НИОКР. Точно так же, риск, обусловленный низкими деловыми качествами менеджеров предприятия, как правило, уже проявился в плохой кредитной истории предприятия и высокой колеблемости его доходов и расходов. Далее, многие виды рисков прямо учитываются в расчетах денежных потоков проекта (например, в виде резервов финансовых средств или расходов на страхование). Во избежание повторного счета связанную с ними “часть премии за риск” необходимо исключать, что на практике сделать обычно не удается;

· этот метод может привести к ошибкам при сравнении вариантов проекта. Если, например, изменить оцениваемый проект, увеличив размеры предусмотренных в нем резервов и запасов, предусмотрев страхование и специальные меры контроля инвесторов за целевым расходованием вложенных средств, его риск явно уменьшится, но пофакторный метод (в известных его вариантах) этого не учтет;

· денежные потоки реального проекта включают не только будущие доходы, но и будущие расходы (капитальные и текущие). Однако, использование повышенной ставки дисконта приводит к ошибкам в учете рисков, связанных с намечаемыми по проекту расходами. Действительно, некоторые из этих расходов — безрисковые, и использование пониженных коэффициентов дисконтирования для них не оправдано. По другим же расходам (например, капитальным) имеется риск их непредвиденного увеличения. При оценке эффективности такие расходы необходимо принимать с более высоким коэффициентом, для чего требуется уменьшать, а не увеличивать ставку дисконта;

· некоторые виды рисков “локализованы во времени”. Например, риск удорожания строительства относится только к периоду строительства, риск отказов оборудования наиболее существенен на этапе освоения этого оборудования и т.д. Учитывать подобные риски, увеличивая ставку дисконта для всего периода реализации проекта, некорректно;

· в ходе проектирования обычно сопоставляются разные варианты проекта. При этом в каждом варианте риск может быть свой. Поэтому при рассматриваемом методе придется сопоставлять варианты проекта с разными ставками дисконта. Оказывается, результат сравнения будет при этом зависеть от того, к какому моменту времени осуществляется приведение денежных потоков.

Ошибки, которые могут быть допущены при использовании данного метода, демонстрируются следующими примерами.

Пример 1. Рискованному проекту А отвечает денежный поток: ‑195, +802, ‑726, +51, +45, +24. Легко проверить, что при ставках дисконта, меньших 180%, этот проект эффективен. Альтернативный проект Б требует инвестиций 195 и дает постоянный гарантированный доход 22 ежегодно в течение неограниченного времени. При безрисковой ставке дисконта 10% проект Б лучше — для него ЧДД=22/0,1‑195=25, тогда как у проекта А ЧДД=18. Учитывая риск проекта А, инвестор решает использовать для его оценки более высокую ставку дисконта 18%. При этом ЧДД увеличивается до 28 и инвестор должен отказаться от более выгодной и к тому же безрисковой альтернативы. n

Пример 2. Проект А безрисковый и ему отвечает денежный поток: ‑3800, +110, +9680. Для его оценки используется безрисковая ставка дисконта 10%. Проект Б отвечает денежный поток: ‑6120, +6348, +6348. Он связан с риском и для его оценки используется ставка дисконта 15%. Если приводить денежные потоки к начальному шагу 0, то проект А оказывается лучше:

‑3800+110/1,1+9680/1,12= 4300 > ‑6120+6348/1,15+6348/1,152= 4200.

Если же приводить денежные потоки к шагу 1 (на котором оба проекта начинают давать доходы), лучшим оказывается проект Б:

‑3800´1,1+110+9680/1,1 = 4730 < ‑6120´1,15+6348+6348/1,15 = 4830. n

Учитывая указанные обстоятельства, применять для реальных инвестиционных проектов подобный способ учета рисков не рекомендуется [52]. Факторы, обычно учитываемые при установлении премий за отдельные виды рисков, более корректно учитывать, надлежащим образом устанавливая умеренно пессимистические значения доходов и расходов проекта или особо рассматривая “рискованные” сценарии. Исключение составляет учет корреляции между неопределенными чистыми денежными притоками проекта и неопределенной доходностью альтернативных вложений в финансовые инструменты (такая корреляция обычно именуется “систематическим риском”), которая может быть учтена количественно излагаемым ниже методом.

2. Использование модели оценки капитальных активов. Иной подход к установлению ставки дисконта реализован в модели оценки капитальных активов (CAPM) и ряде ее модификаций и обобщений. Здесь, по существу, учитывается, что реализация проектов связана с двумя видами неопределенности — внутренней и внешней. Внутренняя относится к самому проекту. Внешняя же неопределенность относится к финансовому рынку в целом и проявляется в (одинаковой для всех участников рынка) неопределенности доходностей разных финансовых инструментов. CAPM дает способ ее учета при установлении ставки дисконта.

CAPM разработана при следующих основных предположениях:

· речь идет о стране с достаточно развитой и стабильной экономикой;

· имеется развитый находящийся в равновесии фондовый рынок, рыночная стоимость финансовых инструментов в целом правильно отражается ценами биржевых сделок;

· финансовые инструменты делимы (т.е. их можно приобрести на любую сумму), а их цены не зависят от объема их покупки;

· имеются вложения, рассматриваемые рынком как безрисковые (до недавнего времени таковыми в США считались казначейские обязательства правительства);

· инвестор имеет возможность занимать деньги и давать их взаймы, причем под одну и ту же процентную ставку r 0, именуемую безрисковой ставкой дисконта;

· доходности всех финансовых инструментов — случайные величины, и всем инвесторам известны их реализации в прошлом и совместное вероятностное распределение в будущем. Зависимости между доходностями различных акций, имевшие место в предыдущем периоде, могут быть распространены и на далекую перспективу.

При этом каждый инвестор формирует оптимальный инвестиционный портфель (с учетом кредитов) на основе своих субъективных предпочтений (в том числе — с учетом своего отношения к рискам), в результате чего на финансовом рынке достигается равновесие: спрос на любые финансовые инструменты совпадет с их предложением.

Все обращающиеся на рынке финансовые инструменты образуют так называемый рыночный (market) портфель. Вложения в него дают случайную доходность x m, в среднем равную rm и имеющую дисперсию D m. В соответствии с CAPM, при некоторых дополнительных ограничениях оптимальным для любого инвестора будет: либо вложить часть средств в безрисковый актив, а остальное — в рыночный портфель (т.е. во все обращающиеся на рынке финансовые инструменты в соответствующей пропорции), либо взять кредит на определенную сумму, после чего вложить собственные и заемные средства в рыночный портфель.

Кроме того, если на рынке обращается финансовый инструмент, дающий на следующем шаге случайную доходность x, то его средняя доходность r связана с доходностью рыночного портфеля формулой (бета-моделью):

,

где — отношение ковариации доходностей данного инструмента и рыночного пакета к дисперсии доходности рыночного пакета, отражающее так называемый систематический риск финансового инструмента[53].

Значения b для отдельных фирм и секторов экономики рассчитываются по ретроспективным данным отдельными исследователями и статистическими службами компаний развитых стран, специализирующихся на рынке информационно-аналитических услуг (например, Value Line), и публикуются.

Традиционно на основе данной модели предлагают устанавливать ставку дисконта как среднюю доходность альтернативных и доступных для инвестора вложений в пакет финансовых инструментов с тем же уровнем систематического риска (b), что и у данного проекта, и дисконтировать по этой ставке средние значения (математические ожидания) денежных потоков проекта, не вводя в них никаких учитывающих риск поправок в виде резервов и запасов. Такое правило хорошо работает для финансовых проектов, но непригодно для оценки проектов в реальном секторе. Это связано с рядом причин.

Прежде всего, в условиях российской экономики ряд исходных предположений CAPM не выполняется:

· российская экономика переходная и нестабильная; устойчивые закономерности между параметрами финансового рынка здесь еще не сложились;

· фондовый рынок не развит, акции многих предприятий недооценены рынком, через биржи проходит незначительная доля сделок и цены этих сделок не всегда и не в полной мере отражают истинную рыночную стоимость акций;

· цена акции существенно зависит от размера пакета покупаемых акций (например, при покупке контрольного пакета стоимость одной акции выше);

· ставки привлечения и размещения займов сильно различаются;

· любые направления вложений инвесторы рассматривают как рискованные;

· высокорискованные вложения нередко являются менее доходными, чем малорискованные;

· наиболее доходными могут быть не только вложения в финансовые инструменты, но и вложения в недвижимость, для которых CAPM неприменима.

Кроме того, денежные поступления и расходы по проекту обычно рассчитываются с учетом определенных резервов и запасов, независимо от того, какими методами после этого будет оцениваться эффективность проекта. Перейти “обратно” от проектных значений параметров проекта к средним при этом практически невозможно.

Для использования CAPM при установлении ставки дисконта в литературе предлагается рассматривать проект как своеобразный финансовый инструмент, а соответствующее значение b принимать таким же, как для акций предприятия, реализующего проект, или “аналогичных предприятий”. Такое предложение базируется на характерной для США форме инвестирования, при которой инвестор вкладывает свои средства не непосредственно в проект, а в акции реализующей его фирмы. Поэтому альтернативными для него будут только вложения в какие-то другие акции. Между тем, в нынешних российских условиях проекты финансируются, как правило, за счет собственных или заемных средств инвестора, для которого альтернативными могут быть вложения не только в акции. Кроме того, неясно, как выбрать “аналогичное предприятие”, если:

· оценивается проект замены одного автопогрузчика другим на заводском складе;

· аналогичных предприятий несколько, и у всех их разные b, или их акции не котируются на рынке, или таких предприятий вообще нет;

· проект лежит вне сферы “нормальной” деятельности предприятия. Например, нефтяная компания оценивает проект создания теплицы для выращивания овощей, отапливаемой добываемым попутным газом. Неясно, надо ли при этом использовать значение b для нефтяных компаний или для тепличных хозяйств?

Важно также иметь в виду, что в России нет достаточно репрезентативных баз данных для проведения столь же масштабных работ по установлению бета-коэффициентов, как в западных странах, и неясно, можно ли использовать значения b, рассчитанные для разных секторов американской или французской экономики, применительно к таким же секторам экономики российской.

Наконец, и это не менее важно, CAPM справедлива только для обращающихся на рынке тиражируемых финансовых инструментов, по которым имеется баланс спроса и предложения (в этом случае вложение в покупку одного такого инструмента дают нулевой ЧДД). Реальные инвестиционные проекты такими инструментами не являются. Поэтому использование CAPM для установления ставки дисконта приводит к ошибкам в расчете интегрального эффекта проекта.

По указанным причинам применять CAPM для установления ставок дисконта для коммерческих структур-участников проекта следует с большой осторожностью, ориентируясь при этом не на умеренно пессимистические, а на средние значения чистых денежных притоков, не вводя при этом в них резервов и запасов. Важно, что при определении средних значений (математических ожиданий) чистых денежных притоков необходимо учитывать принимаемое участниками рынка (а не лицом, оценивающим эффективность проекта) совместное вероятностное распределение этих притоков и доходности рыночного пакета. В то же время для частных акционеров этот метод может использоваться, если результаты его применения согласуются с интересами акционера[54].

Дата добавления: 2015-07-02