Главные центры и медианы графа

Определение. Внутренней медианой графа называется такая его вершина i, для которой минимальна сумма расстояний вершина – вершина. При поиске внутренней медианы минимизируется сумма длин путей, входящих в вершину.

Определение. Внешней медианой графа называется такая его вершина i, для которой минимальна сумма расстояний вершина – вершина. При поиске внешней медианы минимизируется сумма длин путей, выходящих из вершины.

Рассмотрим граф на рис. 1.

; ;

; ;

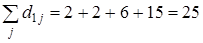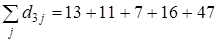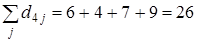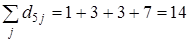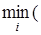; 25; 23; 47; 26; 14)=14, внешняя медиана – вершина 5. Число 14 выделено в табл. 1 жирным шрифтом.

Для графа на рис. 1 имеем

; ;

; ;

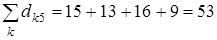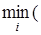; 22; 20; 16; 24; 53)=16, внутренняя медиана – вершина 3. Число 16 выделено в табл. 1 курсивом с подчеркиванием.

Замечание. В общем случае внешние (внутренние) центр и медиана не обязаны совпадать.

Определение. f -точкой на ребре(дуге) (r, s), где 0 ≤ f ≤ 1, называется такая точка ребра(дуги), что расстояние от этой точки до вершины r равно произведению (рис. 2).

Например, 0-точка ребра (дуги) (r, s) – это вершинa r; 1-точка – это вершина s; 0,5-точка – это середина ребра (дуги) (r, s).

Определение. Расстоянием вершина-ребро (дуга) (обозначение:

d (i, (r, s)) называется длина кратчайшего пути от данной вершины i до самой удаленной от вершины i f- точки на данном ребре (дуге) (r, s).

Выведем формулу для расчета величины d(i, (r, s))

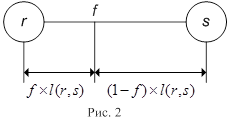
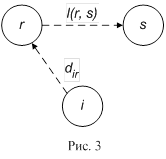Случай 1. (r, s) – дуга (рис. 3).

Самой удаленной от вершины i точкой на дуге

(r, s) будет точка, бесконечно близкая к вершине

s слева. Чтобы пройти в эту точку нужно из

вершины i пройти в вершину r (по кратчайшему

пути длины d(i, r)), а затем пройти всю дугу (r, s).

Следовательно

(1)

Случай 2. (r, s) – ребро (рис. 4).

Если (r, s) – ребро, то есть два

способа пройти из вершины i в

точку на ребре (r, s).

Способ 1. из вершины i в вершину r (длина кратчайшего пути равна

d_ir), затем по ребру из вершины r в f -точку (длина части ребра равна ).

Способ 2. из вершины i в вершину s (длина кратчайшего пути равна d_is), затем по ребру из вершины s в f -точку (длина части ребра равна ).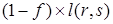

Выбирается кратчайший путь, поэтому самой удаленной f- точкой на ребре (r, s) от вершины i будет такая точка, для которой оба названных пути равны по длине. Следовательно, само расстояние вершина-ребро (дуга) равно

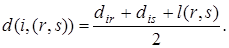(2)

Таким образом,

(3)

Расстояния вершина-ребро (дуга) образуют матрицу D ₁ расстоянийвершина-ребро (дуга). В этой матрице p строк и q столбцов (табл. 2).

В табл. 2 дуги обозначены стрелками над номерами вершин, которые эта дуга соединяет. В табл. 2 показаны расстояния вершина-ребро (дуга) для графа на рис. 1.

Например,

Таблица 2

			(1,2)	(2,4)	(3,4)		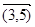(4,5)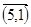
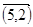
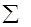
					7,5					87,5
D 1 =					7,5					83,5
					8,5					55,5

На рис. 1 показана наиболее удаленная от вершины 5 f- точка ребра (3,4). Эта точка лежит на расстоянии 5,5 от вершины 3 и на расстоянии 1,5 от вершины 4 (5,5+1,5 = 7 = l (3,4)).

Определение. Главным внешним центром графа называется такая его вершина i, для которой достигается минимум максимальных расстояний вершина-ребро (дуга). В табл. 2 максимальные расстояния

d (i- (r, s)), i = 1,2,3,4,5выделены в каждой строке жирным шрифтом.

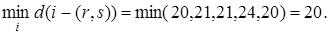
В этом графе два главных внешних центра – вершины 1 и 5. Числа 20 (в первой и пятой строках табл. 2) выделены жирным курсивом.

Определение. Главной внешней медианой графа называют такую его вершину, для которой минимальна сумма расстояний вершина-ребро (дуга).

В нашем случае (табл. 2) min(87,5; 83,5; 117; 82; 55,5)=55,5. Главная внешняя медиана – это вершина 5. Число 55,5 выделено в табл. 2 жирным шрифтом.

Замечание. В общем случае центры, медианы, главные центры и главные медианы не обязаны совпадать.

Определение. Расстоянием ребро (дуга) – вершина (обозначение: d ((r, s), i)) называется длина кратчайшего пути до вершины i от самой удаленной от этой вершины f- точки на дуге (ребре) (r, s).

Выведем формулу для расчета числа d ((r, s), i).

Случай 1. (r, s) – дуга (рис. 5).

Если (r, s)– дуга, то самый длинный путь до вершины i – это путь из бесконечно близкой справа к вершине r f- точки. Длина этого пути равна

l (r, s) +d_si.

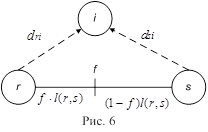Случай 2. (r, s)– ребро (рис. 6). Из всякой f- точки на ребре (r, s) есть два пути в вершину i: через вершину r и через вершину s. Нужно выбрать кратчайший из этих двух путей. Следовательно, вершина i удалена более всего от той f- точки, до которой оба пути до вершины i равны по длине и равны величине

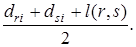
Итак, (4)

Расстояния ребро (дуга) – вершина образуют матрицу D ₂расстояний ребро (дуга) – вершина. В этой матрице p строк и q столбцов (табл. 3). В табл. 3 показаны расстояния ребро (дуга) – вершина для графа на рис. 1.

Например,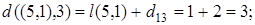

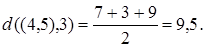
Определение. Главным внутренним центром графа называют такую его вершину, для которой минимально максимальное расстояние ребро (дуга) – вершина. В табл. 3 максимальные расстояния 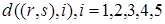выделены в каждом столбце жирным шрифтом.

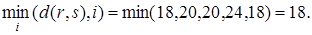
В графе два главных внутренних центра – вершины 1 и 5. Числа 18 в табл. 3 выделены также курсивом.

Определение. Главной внутренней медианой графа называется такая его вершина, для которой минимальна сумма расстояний ребро (дуга) – вершина.

В нашем случае min(70, 66, 62, 74, 122)=62; главная внутренняя медиана – это вершина 3. Число 62 выделено в табл. 3 жирным шрифтом.

Таблица 3

D 2 =	Вершина Ребро(дуга)
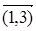
(1,2)
(2,4)			7,5
(3,4)
(4,5)			9,5
∑

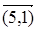
Дата добавления: 2015-07-02