Вычисление собственных значений матрицы

Планшетного компьютера, камеры) и принести запись

Для участия в Конкурсе необходимо снять любой ролик

Объявляется конкурс: SCARY MOVIE

Приносите свои рисунки, куклы и прочие поделки в Администрацию Центра до 3 ноября.

Конкурс: crafts for Halloween.

Для групп уровней Junior, Beginner, Elementary объявляется

Внимание!!! Конкурс!

С 28 октября по 3 ноября

Для групп уровней Pre-Intermediate, Intermediate,

Upper-Intermediate, Advanced, подготовка к FCE

на тему Halloween (с помощью мобильного телефона,

в Администрацию Центра или выслать по адресу [e-mail] до 5 ноября.

Победители будут отмечены призами. Все участники получат баллы в зачет бонусной системы.

Целый ряд инженерных задач сводится к рассмотрению систем уравнений, имеющих единственное решение лишь в том случае, если известно значение некоторого входящего в них параметра. Этот особый параметр называется характеристическим, или собственным, значением системы.

Алгоритмы решения задач на собственные значения делятся на две группы. Итерационные методы очень удобны и хорошо приспособлены для определения наименьшего и наибольшего собственных значений. Методы преобразований подобия несколько сложней, зато позволяют определить все собственные значения и собственные векторы.

Рассмотрим матрицу n-го порядка:

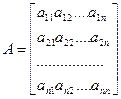
Вектор x=(x₁,x₂,…,x_n) называется собственным вектором матрицы А, соответствующим собственному значению l, если он удовлетворяет системе уравнений: Аx=lx.

Поскольку при умножении собственного вектора на скаляр он остается собственным вектором той же матрицы, то его можно нормировать. В частности, каждую координату собственного вектора можно разделить на максимальную из них или на длину вектора, в последнем случае получится единичный собственный вектор.

Характеристической матрицей С данной матрицы А называется матрица вида

,

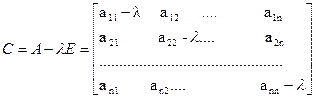где λ– собственное значение, Е- единичная матрица.

Тогда систему уравнений можно записать так: (A-lE)x=0 или Cx=0.

Если перейти к координатной форме записи вектора x, то систему можно записать в виде

.

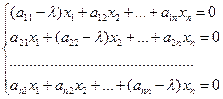Эта система имеет ненулевое решение лишь тогда, когда ее определитель равен 0: det(A-λE)=0. Причем решение не единственно. Так как обычно одно уравнение является следствием остальных.

Определитель матрицы С является многочленном n-ой степени относительно λ: det C=c₀ λⁿ+ c₁ λ^n-1+ ….+ c_n-1 λ¹+ c_n λ⁰ - характеристический многочлен.

Корни этого многочлена являются собственными значениями матрицы А.

Пример 1

Вычислить собственные числа и собственный вектор матрицы .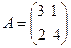

Составим характеристический многочлен: .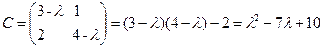

Найдем корни этого многочлена: λ₁=2, λ₂=5.

Для нахождения собственных векторов x₁, x₂ составим соответствующие системы уравнений вида Ax=λx:

При λ₁=2 получим 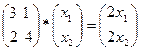или в виде системы уравнений: 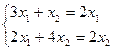. Преобразовав, получим: .

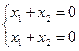Уравнения линейно зависимы, даже совпадают. Поэтому оставляем одно из них.

Полагаем x₁=1. Тогда x₂=-1.

Тогда собственный вектор, соответствующий λ₁=2, имеет вид x₁ =(1,-1).

Аналогично находим второй собственный вектор, соответствующий значению λ₂=5 – x₂ =(1,2)

В общем случае, особенно для матриц высокого порядка, задача нахождения их собственных значений и векторов, называемая полной проблемой собственных значений, значительно более сложная.

Часто в практических вычислениях бывают нужны не все собственные значения, а лишь некоторые из них. В этих случаях нецелесообразно решать полную проблему собственных значений.

Для решения частичной проблемы собственных значений обычно используют итерационные методы. Итерационный процесс строится на применении методов итерации к решению системы уравнений AХ = λ Х.

Дата добавления: 2015-07-02