
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение наименьшего собственного значения методом итераций
|
|
|
|
В некоторых случаях целесообразно искать наименьшее, а не наибольшее собственное значение. Это можно сделать, предварительно умножив исходную систему на матрицу, обратную A:
А-1А X =λА-1 X.
Если обе части этого соотношения умножим на 1/λ и учитывая, что АА-1=Е, то получим 1/λ Х = A-1 X.
Ясно, что это уже иная задача на собственное значение, для которой оно равно 1/λ, а рассматриваемой матрицей является A-1. Максимум 1/λ, достигается при наименьшем λ. Таким образом, описанная выше итерационная процедура может быть использована для определения наименьшего собственного значения новой системы.
Определение собственных значений методами преобразований подобия
Метод преобразований подобия применяется с целью получить из исходной матрицы новую с теми же собственными значениями, но более простого вида. Очевидно, самым лучшим упрощением было бы приведение матрицы к чисто диагональному виду, так как в этом случае собственные значения просто соответствовали бы элементам матрицы, стоящим на главной диагонали.
Очевидно, самым лучшим упрощением матрицы было бы приведение ее к треугольному виду
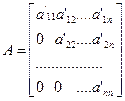 . Тогда
. Тогда 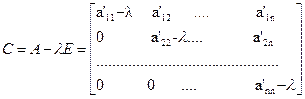 .
.
Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен в этом случае имеет вид: det C=(a’11-λ)(a’22-λ)…(a’nn-λ).
Собственные значения матрицы, равные корням этого многочлена можно сразу получить: λ1=a’11, λn=a’22, …,, λn=a’nn.
Т.о., собственные значения треугольной матрицы равны ее диагональным элементам. То же самое, естественно, относится и к диагональной матрице, которая является частным случаем треугольной.
Задачи для самостоятельного решения:
Задача 1
Найти собственные значения и собственные вектора матриц
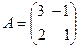
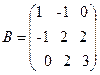
Задача 2
Решить методом простой итерации систему уравнений с точностью ε=10-3.
a) 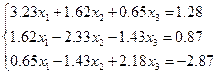
b) 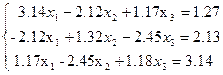
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 658; Нарушение авторских прав?; Мы поможем в написании вашей работы!