Определение наибольшего собственного значения методом итераций

Итерационные методы решения

Процедура начинается с пробного нормированного вектора X⁽⁰⁾ – начальное приближение собственного вектора X, причем собственные векторы на каждой итерации нормированы.

Итерационный процесс запишется в виде λ⁽ⁱ⁺¹⁾X⁽ⁱ⁺¹⁾=AX⁽ⁱ⁾, где i=0,1,2,…

Подставляя в правую часть этой системы вектор X⁽⁰⁾, получаем некоторый вектор Y⁽¹⁾. После нормировки этого вектора он представится в виде Y⁽¹⁾=λ⁽¹⁾ X⁽¹⁾, где λ⁽¹⁾ – первое приближение собственного значения, X⁽¹⁾ – нормированный вектор. Теперь нужно X⁽¹⁾ снова подставить в правую часть системы и найти новые приближения λ⁽²⁾ и X⁽²⁾. Итерационный процесс продолжается до установления постоянных значений λ и X. При этом найденное число λ – наибольшее по модулю собственное значение матрицы, а X – соответствующий ему собственный вектор.

Быстрота сходимости этого итерационного процесса зависит от того, насколько удачно выбран начальный вектор. Если он близок к истинному собственному вектору, то итерации сходятся очень быстро. На быстроту сходимости влияет также и отношение величин двух наибольших собственных значений. Если это отношение близко к единице, то сходимость оказывается медленной.

Пример 2

Найдем максимальное собственное значение матрицы .

1. Возьмем начальное приближение X⁽⁰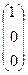⁾= и подставим его в правую часть итерационного уравнения: .

2. Нормируем вектор Y⁽¹⁾, разделив его на макс.координату: λ⁽¹⁾=10, .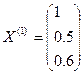

Результаты вычислений запишем в виде таблицы:

№ итерации	Собственное значение λ^(^i^)	Собственный вектор X
X1	X2	X3
			0.5	0.6
		0.61923	0.66923
	36.392	0.42697	0.56278
	34.813	0.37583	0.49954
	34.253	0.35781	0.46331
		0.34984	0.4428
	33.87	0.3458	0.43121
	33.8	0.34362	0.42466
	33.76	0.3424	0.42094
	33.738	0.34171	0.41884
	33.726	0.34132	0.41765
	33.719	0.3411	0.41697
	33.714	0.34093	0.41658
	33.712	0.34091	0.41636

Отметим, что для достижения требуемой точности потребовалось 14 итераций.

Дата добавления: 2015-07-02