Расчет коэффициента ассоциации

Расчет коэффициента конкордации

Эксперт						б
А
Б					5,5			5,5
В
Г
					22,5			24,5
d	-19	-14	-9	-12	0,5			2,5
d^2					0,25			6,25		225∑d^2= 1177,5

Таблица 10

Критерий	Лучшие	Отчисленные	Сумма (Νχ)
I	α = 75	b= 16	a +b = 91
IV	с= 14	d= 68	c + d=82
Сумма (Nv)	а + с = 89	b + d = 84	N= 173

Рассмотрим пример вычисления коэффициента ассоциации при изучении связи между такими критериями пригодности, как 1 и IV группы, и критериями успешности обучения – лучшие и отчисленные:

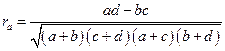
где а, b, с, d– численности альтернативных признаков (практически неограничены).

В корреляционной решетке (табл. 10) приведены исходные данные для расчетов (х– группа; у – успешность обучения).

Подставляя в формулу соответствующие значения из таблицы, находим величину коэффициента ассоциации (r_a = 0,65), который выражается в долях от 0 до 1. Достоверность оценивается по его отношению к средней ошибке, определяемой по формуле

откуда t= 16,25

Достоверность r_а может быть определена также и по специальным таблицам [52].

При изучении корреляционной зависимости между вариационными рядами с отсутствием линейной зависимости более правомерным является вычисление корреляционного отношения, которое измеряет состояние любых, в том числе и нелинейных, связей между признаками.

В отличие от коэффициента корреляции, изучающего двустороннюю связь между x и у, корреляционное отношение (η) показывает только зависимость изменений второго (у) признака от изменений первого (х), или наоборот Корреляционное отношение – величина относительная, положительная и принимает значение от 0 до 1. Показатели корреляционного отношения обычно не равны между собой – η_y/x ≠ η_x/y Они определяются по следующим формулам:

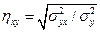и , где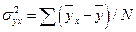

– среднее квадратическое отклонение частотных или групповых средних величин (ух), то есть частная дисперсия;

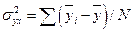– общая дисперсия совокупности.

Эти формулы можно выразить и в другом виде:

;

;

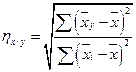
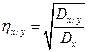
По приведенным формулам удобно определять коэффициенты корреляционного отношения для небольших выборок, а при наличии большого числа наблюдений необходимо предварительно весь материал группировать в вариационные ряды и вносить в корреляционную таблицу.

Рассмотрим вычисление корреляционного отношения на выборке из 10 наблюдений (табл. 11)

Сначала находим коэффициент корреляционного отношения полетов у по грубым ошибкам х, то есть η _/х, для чего ранжируем выборку по x (значения x расположены в возрастающем порядке сверху вниз). Затем определяем вспомогательные величины для вычисления корреляционного отношения по x и подставляем в формулу, откуда η_γ/χ = 0,99.

Таблица11

Дата добавления: 2015-07-02