Алгоритм. Алгоритм состоит из двух этапов: первого – этапа обучения, во время которого накапливается информация о признаках на основании уже имеющегося опыта и

Алгоритм состоит из двух этапов: первого – этапа обучения, во время которого накапливается информация о признаках на основании уже имеющегося опыта и оценивается информативность выбранных признаков, и второго – этапа классификации, на котором выносится решение о пригодности субъекта к определенной деятельности.

Обучение. Предполагается, что на основании предыдущего опыта можно выделить группы субъектов «А» и «В», которые отражают наше понимание пригодности (или непригодности) к данной деятельности и являются определенными эталонами для дальнейшего прогнозирования пригодности. Ряд практических вопросов, связанных с образованием классов «А» и «5», будет рассмотрен ниже. Далее предполагается, что имеется какой-то набор признаков ν₁, ν₂,..., ν_n, существенность которых для определения профессиональной пригодности можно и не знать. Теперь можно построить множество векторов {ν_Α} и {v_B}, соответственно характеризующих группы субъектов «А» и «В».

Процесс обучения состоит в получении оценки дискрет ных одномерных распределений вероятностей признаков ν₁, ν₂,..., ν_n для класса «А»: для класса «В»: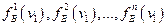

Предполагается, что ν₁, ν₂,..., ν_n слабо зависимы. Если, однако, этого нет, то для увеличения эффективности процедуры в рассмотрение вводятся сложные признаки – синдромы, определение которых можно получить на основании опыта и теоретических соображений или же используя соответствующий математический аппарат. Построение одномерных распределений существенно облегчает процесс обучения, а в случае слабой зависимости потери информации при этом невелики.

Если классы «А» и «В» многочисленны, то можно получить достаточно хорошую оценку требуемых вероятностей

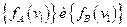(i=1,2,…,n)

В тех же случаях, когда численности классов «А» и «В» невелики, приходится прибегать к грубому квантованию признаков на 2–3–4 градации. Практическая проверка показывает, что при наличии в группе 25–30 человек и соответствующем квантовании можно получить удовлетворительные результаты.

Полученные в результате обследования данного контингента лиц показатели могут иметь различную ценность для целей прогнозирования профессиональной пригодности. Поэтому следующим этапом «обучения» является оценка информативности признаков.

Признак будет тем более информативным, чем больше различие между его распределениями у представителей класса «А» и «В». Оценка информативности признака ν, может выражаться величиной Ρ_j – вероятностью того, что распределения 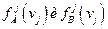различны. Это достигается при помощи вычисления χ ². Интуитивно ясно, что вероятность Ρ может быть хорошей мерой информативности признака ν при данной конкретной классификации. Необходимо отметить, что признаки, информативные в одном случае, могут оказаться совсем не информативными для решения задачи профотбора других специалистов.

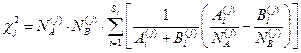
Вычисление с² производилось по формуле:

где 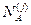и 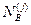– общее число лиц соответственно в классах «А» и «В», данные которых использовались при построении распределений для j -го признака; и 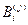– частоты появления индивидов в i -йрадации j-го признака для сравниваемых классов; S – число градаций для j-го признака.

Вероятности Ρ_jпределялись по таблицам Л. Большова и Н. Смирнова [52]. Оценка информативности может быть также получена и при помощи расстояния Кульбака. В принятых здесь обозначениях и несколько измененной форме это расстояние имеет вид:

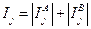
где

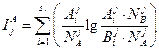и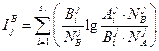

Эта мера имеет ряд преимуществ, особенно при теоретических исследований. Для практики представляет интерес возможность измерения значимости признаков ν₁(j= 1, 2,...,n) отдельно для вынесения решения о принадлежности ν к {ν_Α} или {v_B} (соответственно слагаемые 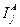и ).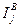

Используя ту или другую меру, признаки целесообразно расположить по их убывающей информативности, а те из них, которые неинформативны (Р слишком велико или I - мало), использовать не надо. Если окажется, что информативных признаков осталось мало, то необходимо ввести новые признаки.

Процесс «обучения» можно считать законченным, когда оценки распределений и 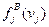(j= 1, 2,..., n ) достаточно надежны, признаки упорядочены по их информативности и их достаточно много.

Классификация (решающее правило). При классификации можно допустить две ошибки. Субъект из класса «А» может быть ошибочно отнесен к классу «B» и, наоборот, субъект из класса «B» может быть ошибочно причислен к классу «А». Первую из указанных ошибок классификации будем обозначать через α, а вторую через β.

Вероятности ошибок а и β определяются до проведения классификации. При выборе этих вероятностей должна быть учтена важность той или другой ошибки классификации, а также реальная ситуация, возникшая при решении данной конкретной задачи.

Пусть при обследовании субъекта S были получены признаки 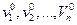(они приведены здесь в порядке их убывающей информативности). Пусть на основании здравого смысла выбраны допустимые вероятности ошибок α и β. Рассмотрим отношение вероятностей, соответствующих первому признаку:

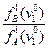
Если это отношение бeдет меньше чем:

то это будет означать, что полученное значение признака настолько вероятнее для класса «А», что можно с выбранным уровнем надежности (α, β) утверждать, что данное лицо относится к классу «А» (пригодно к данной профессиональной деятельности). Если это отношение

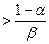
то с тем же уровнем надежности принимается решение о непригодности к рассматриваемой деятельности.

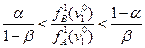
то информация, заключенная в признаке, недостаточна для отнесения к классам «А» и «B» и рассматривается следующий признак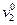

Если

то выносится решение об отнесении индивида в класс «А» если

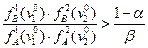
то в класс «В». Когда же

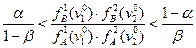
то рассматривается значение третьего признака и т. д.

Если, перебрав все признаки, не удается отнести субъекта к тому или иному классу с данным уровнем надежности, то есть рассматриваемое отношение не выходит за пределы требуемых рубежей, то это означает, что имеющиеся результаты обследования не позволяют сделать прогноз с выбранным уровнем надежности. В этих случаях можно понизить этот уровень и таким образом сделать прогноз или обратиться за дополнительной информацией.

При отсутствии дополнительной информации для минимизации вероятности ошибки целесообразно построить два распределения отношения правдоподобия по всем признакам соответственно для групп «А» и «В» и на основе этих распределений выбрать один порог. Особенности распределения обычно таковы, что этим порогом редко бывает 1.

Как известно, в схемах последовательного статистического анализа [58] процедуры обосновываются для однородного случая, когда

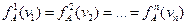и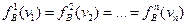

Однако нетрудно показать, что зависимость порогов от вероятности ошибок α и β переносится и на случай неоди наковых распределений, возникающих в диагностической задаче.

Практически удобно иметь дело не с отношениями вероятностей, а с логарифмом этого отношения. Тогда все вычисления сводятся к последовательному сложению.

Итак, определение принадлежности векторов ν (ν₁, ν₂,..., ν_n) к множеству {ν_Α} или {ν_Β} осуществляется следующим образом. Последовательно вычисляются величины L₁ L₂,..., L_k, где:

Каждое вычисленное L_k сравнивается с порогами

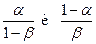
Если пр некотором k<n

То вычисляется L_k+1. Если же

То 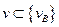; если же

Дата добавления: 2015-07-02