Линейная регрессия

Вычисление и анализ приближенной регрессии.

Принцип наименьших квадратов позволяет полностью вычислить уравнение приближенной регрессии заданного типа (с неопределенными коэффициентами). Для этого вначале составляется сумма

,

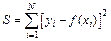где функция 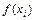записана со всеми неопределенными коэффициентами 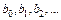. Величину 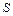можно теперь рассматривать как функцию от этих неопределенных коэффициентов. Задача заключается в определении коэффициентов, минимизирующих величину .

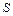Необходимым условием минимума дифференцируемой функции многих переменных 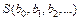является выполнение условия

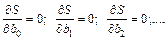
После дифференцирования получаем систему нормальных уравнений:

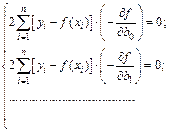
Рассмотрим построение уравнения регрессии вида .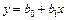

Пользуясь принципом наименьших квадратов, легко составить нормальные уравнения линейной регрессии:

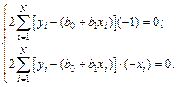
Делая простые преобразования, приводим эту систему к виду

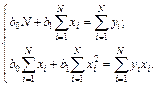
Систему уравнений решаем с помощью определителей:

,

где

;

;

;

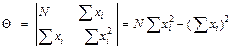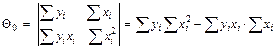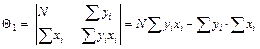откуда

.

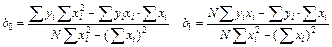Коэффициент 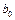проще определяется из первого уравнения системы как

.

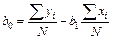Для оценки адекватности полученного уравнения регрессии по критерию Фишера сравниваем общую дисперсию 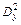с остаточной дисперсией 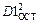. Критерий Фишера показывает, во сколько раз уравнение регрессии 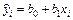описывает экспериментальные данные лучше, чем среднее значени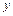е (т.е. ).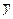

где 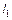– число коэффициентов в уравнении регрессии (в данном случае );

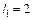Уравнение адекватно описывает экспериментальные данные, если расчетное значение критерия Фишера

,

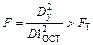где 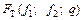– табличное значение критерия Фишера, найденное по таблицам при степенях свободы 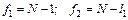и уровне значимости .

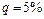Дата добавления: 2015-07-02