Параболическая регрессия

Рассмотрим построение уравнения регрессии вида .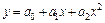

Составление системы нормальных уравнений для нахождения коэффициентов параболической регрессии осуществляется аналогично составлению нормальных уравнений линейной регрессии.

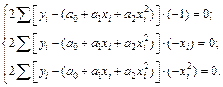
После преобразований получаем:

.

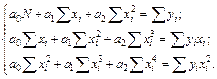Решая систему нормальных уравнений, получают коэффициенты уравнения регрессии.

Далее рассчитывают остаточную дисперсию .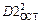

,

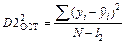где 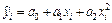, а .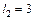

Уравнение второй степени значимо лучше описывает экспериментальные данные, чем уравнение первой степени, если уменьшение дисперсии 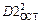по сравнению с дисперсией линейной регрессии 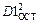является значимым (неслучайным). Значимость различия между 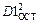и 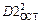оценивается критерием Фишера:

,

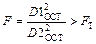где число 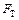берется по справочным статистическим таблицам (приложение 1) соответственно степеням свободы 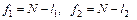и выбранного уровня значимости .

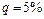Порядок выполнения расчетной работы:

1. Ознакомиться с теоретическим материалом, изложенным в методических указаниях либо в дополнительной литературе.

2. Рассчитать коэффициенты линейного уравнения регрессии 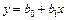. Для этого необходимо вычислить суммы 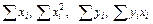. Удобно сразу вычислить суммы 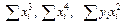, которые пригодятся для расчета коэффициентов параболического уравнения.

3. Вычислить расчетные значения выходного параметра по уравнению .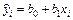

4. Вычислить общую и остаточную дисперсии 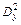, , 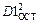а также критерий Фишера .

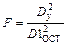5. Рассчитать коэффициенты параболического уравнения регрессии 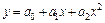. Учитывая сложность решения системы нормальных уравнений, рекомендуется записать систему нормальных уравнений в матричной форме:

,

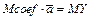где 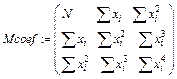– матрица, элементами которой являются коэффициенты системы нормальных уравнений;

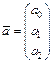– вектор, элементами которого являются неизвестные коэффициенты;

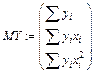– матрица правых частей системы уравнений.

6. Далее решить эту систему линейных уравнений в среде MathCad. Для этого воспользоваться стандартной функцией для решения системы линейных уравнений .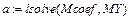

7. Вычислить расчетные значения выходного параметра по уравнению .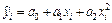

8. Вычислить остаточную дисперсию 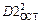, а также критерий Фишера .

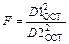9. Сделать выводы.

10. Построить графики уравнений регрессии и исходных данных.

11. Оформить расчетную работу.

Дата добавления: 2015-07-02