Сходимость тригонометрического ряда Фурье по нормам функциональных пространств [2]

Теорема [1]. Если функция f с периодом абсолютно непрерывна, а ее производная, то ряд Фурье функции f сходится к ней равномерно на всей прямой.

Напоминания. Ряд Фурье в гильбертовом пространстве всегда сходится. По теореме Вейерштрасса тригонометрические полиномы образуют всюду плотное множество в 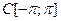, а 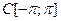всюду плотно в . Следовательно, тригонометрическая система образует полную ортонормированную (с множителем ) систему в . Итак, всякая функция есть сумма своего ряда Фурье, сходящегося к f в среднем квадратичном (и почти всюду с учетом результата Карлсона).

Ряды по функциям можно строить и изучать в разных нормированных пространствах функций на отрезке 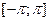. Мы ограничимся важным классом пространств, содержащим большинство тех, которые используются в аналитических применениях.

Определение. Нормированное пространство 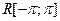называется однородным пространством функций, если выполняются условия:

1) и из сходимости по норме 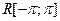вытекает сходимость в .

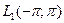2) Если f(x) продолжается с периодом 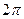на всю ось x, то при любом вещественном h 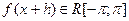и .

3) Тригонометрические многочлены 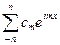образуют всюду плотное множество в .

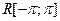Этим условиям удовлетворяют многие известные функциональные пространства: 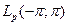при ; в 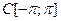не выполнено условие 2), так как непрерывная функция f(x) при перестает быть непрерывной после периодического продолжения на всю ось и, например, 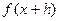уже не входит в 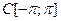. Но подпространство , выделенное условием 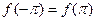, уже удовлетворяет всем условиям 1) – 3). Аналогично, подпространство , выделяемое условием , также удовлетворяет условиям 1) – 3).

Установим, прежде всего, вид тригонометрического ряда в однородном пространстве 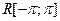. Нам понадобится только условие 1).

Дата добавления: 2015-07-02