Гильбертовы пространства

Часть 2.

Пусть H – линейное пространство над полем комплексных чисел C (или в частном случае над полем действительных чисел R), в котором задано скалярное произведение :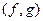

1) ,

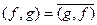2) 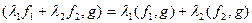для любых элементов из поля,

3) ,

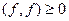4) .

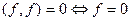Скалярное произведение порождает в пространстве H норму: .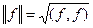

Пространство со скалярным произведением называется гильбертовым, если оно является полным относительно нормы, порожденной скалярным произведением.

Примеры гильбертовых пространств.

1) Пространство , элементами которого являются упорядоченные наборы из n комплексных чисел: 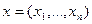. Скалярное произведение элементов x и y в этом пространстве задается равенством .

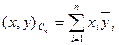2) Пространство 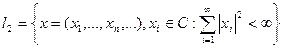со скалярным произведением .

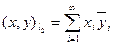3) Пространство 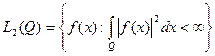функций, определенных почти всюду в области 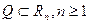, квадрат модуля которых имеет в этой области конечный интеграл Лебега. Здесь скалярное произведение и порожденная им норма имеют вид: , .

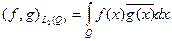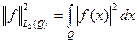Пусть Q – ограниченная область. Из теории интеграла Лебега известно, что пространство непрерывных в замыкании области Q функций 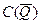всюду плотно в 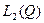. Это пространство с нормой равномерной сходимости 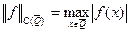банахово, то есть полное нормированное пространство. Известна теорема Вейерштрасса: для любой непрерывной на компакте функции 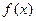существует последовательность многочленов 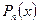, которая сходится к этой функции в равномерной метрике.

Напомним, топологическое пространство называется сепарабельным, если в нем существует счетное всюду плотное множество.

В 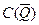счетное, всюду плотное множество образуют многочлены с рациональными коэффициентами. Так как 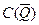всюду плотно в 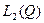, то многочлены с рациональными коэффициентами образуют счетное всюду плотное множество также и в .

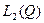Определение. Система элементов 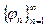ортогональна в гильбертовом пространстве Н, если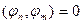 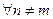. Если, кроме того, 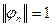, то это ортонормированная система:

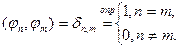
Определение. Систему элементов 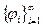называют полной в пространстве Н, если ее линейная оболочка всюду плотна в этом пространстве: .

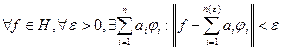Утверждение. В сепарабельном гильбертовом пространстве существует полная ортонормированная система.

Доказательство. Н – сепарабельное, значит, существует счетное всюду плотное множество 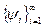. Построим по нему полную ортонормированную систему .

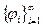Возьмем первым элементом 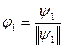. Из 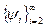выберем произвольный элемент, не пропорциональный 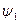. Пусть это будет 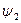, по нему определим ортогональный к 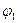элемент: 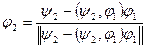. Затем из системы 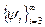выберем элемент, линейно независимый с парой 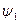, 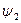(в бесконечномерном пространстве такой выбор возможен, так как иначе система 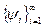лежит в конечномерном подпространстве и, значит, не может быть всюду плотной). По выбранному элементу 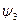определяем элемент, ортогональный к 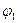, 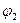: 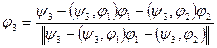. Процесс этот бесконечен (в конечномерном пространстве удастся построить ортонормированную систему, число элементов которой будет равно размерности пространства). Отметим, в этом процессе элемент 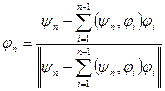является линейной комбинацией n элементов исходной системы 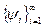, а значит, линейные оболочки обеих систем совпадают: 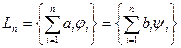. Последнее означает полноту построенной ортонормированной системы.

Утверждение доказано.

Пусть 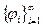– ортонормированная система в гильбертовом пространстве Н, 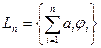– линейная оболочка первых n элементов этой системы. Поставим задачу: для конкретного элемента 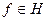найти ближайший к нему элемент из конечномерного подпространства 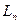. То есть необходимо решить задачу минимизации функции 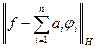конечного числа скалярных аргументов 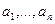. Рассмотрим квадрат этой функции:

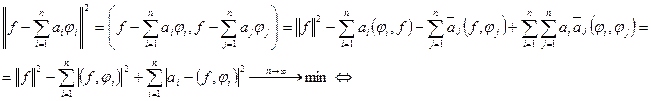
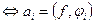– коэффициент Фурье элемента 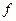по ортонормированной системе .

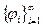Таким образом, доказана

Теорема. Ближайший к 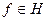элемент линейной оболочки 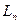с ортонормированным базисом 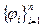определяется коэффициентами Фурье: .

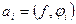Отметим, что попутно доказано неравенство Бесселя: 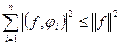. Действительно, если считать 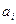уже выбранными как коэффициенты Фурье, то, учитывая неотрицательность нормы, получим

,

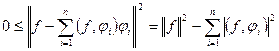что равносильно неравенству Бесселя.

Из неравенства Бесселя следует сходимость числового ряда 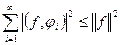. А это значит, что последовательность коэффициентов Фурье 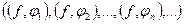принадлежит пространству .

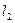Пусть в гильбертовом пространстве Н выбрана счетная ортонормированная система 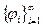, каждому элементу 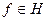можно поставить в соответствие ряд с коэффициентами Фурье 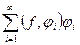, который называют рядом Фурье элемента .

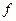Теорема. Ряд Фурье в гильбертовом пространстве всегда сходится.

Доказательство. Достаточно показать, что частичные суммы этого ряда 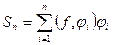образуют фундаментальную последовательность. Пусть 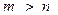, рассмотрим .

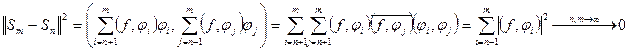Стремление к нулю следует из сходимости соответствующего числового ряда.

Теорема доказана.

Утверждение. Ортонормированная система элементов 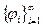гильбертова пространства Н является полной в этом пространстве тогда и только тогда, когда выполнено одно из условий:

1) Для любого элемента 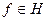ряд Фурье, построенный по 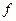, сходится к этому элементу в пространстве Н.

2) Для любого элемента 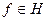справедливо равенство Парсеваля .

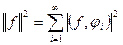3) Если для какого-то элемента 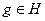все его коэффициенты Фурье 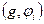равны нулю, то 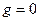в Н.

Доказательство эквивалентности этих условий предлагается в качестве упражнения.

Итак, в сепарабельном гильбертовом пространстве существует счетная, полная ортонормированная система. Это значит, что каждый элемент пространства раскладывается в ряд Фурье по этой системе.

Теорема. Все сепарабельные гильбертовы пространства изоморфны и изометричны пространству .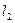

Определение. Н изоморфно 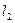, если существует взаимно однозначное отображение этих пространств, сохраняющее линейные операции. Изометрия означает, что при этом отображении сохраняются нормы.

Доказательство. Каждому элементу 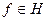поставим в соответствии последовательность его коэффициентов Фурье 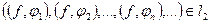по полной ортонормированной системе 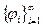. Линейность такого отображения очевидна, а сохранение норм – это равенство Парсеваля.

Теорема доказана.

Замечание. Если система 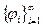ортогональна, но не нормирована в Н, то коэффициенты Фурье элемента 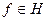имеют вид .

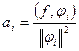Дата добавления: 2015-07-02