Определение коэффициентов ряда Фурье

Пусть функция f(x) разлагается в тригонометрический ряд Фурье в интервале (0, 2π).

(1) f(x) = 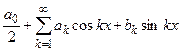(0 < x < 2π)

Определим коэффициенты a_k и b_k (можно доказать, что тригонометрические ряды можно почленно интегрировать).

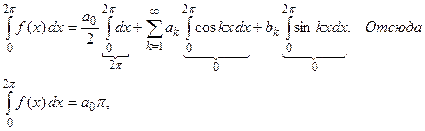
Умножим (1) на cos nx и проинтегрируем.

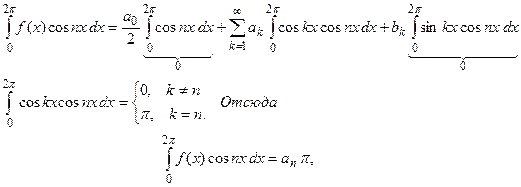
Умножив (1) на sin nx, найдем

Коэффициенты a_k и b_k называются коэффициентами Фурье.

Если функция f(x) определена на интервале (-π; π), то коэффициенты ряда Фурье определяются по формулам

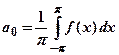
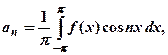
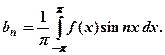
П р и м е р. Разложить функцию f(x) в ряд Фурье в интервале (0, 2π). Построить график суммы ряда.

f(x)

-π 0 π 2π 3π x

-1

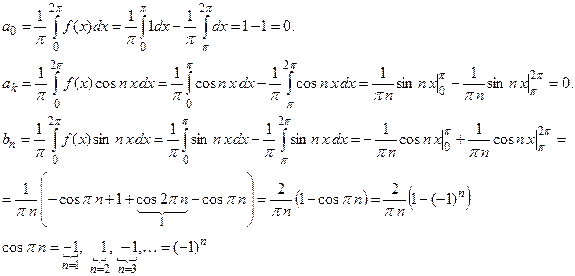
При x Є (0, 2π) сумма ряда совпадает с функцией f(x). Но сумма ряда является периодической функцией и определена на всей числовой оси, а не только на интервале (0, 2π). Для построения графика суммы ряда надо периодически продолжить график функции f(x) на всю числовую ось.

О сходимости ряда Фурье.

Можно показать, что в точках, где функция f(x) непрерывна, сумма ряда Фурье совпадает со значениями функции f(x), а в точках разрыва функции f(x) ряд Фурье сходится к среднему арифметическому ее предельных значений, т.е., если x = x₁ – точка разрыва функции f(x), то ряд Фурье сходится к значению

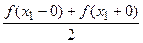
f(x)

● ● ●

x

Ряды Фурье для функций, заданных в интервале (-l, l).

Пусть функция f(x) определена в интервале (-l, l). Введем новую переменную t так, чтобы эта функция от t была задана в интервале (-π, π)

Тогда, если –l < x < l, то -π < x < π. Функцию f (^l∙t/_π) разложим в ряд Фурье в интервале
(-π, π).

Возвратимся к старой переменной x.

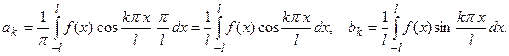
П р и м е р. Разложить функцию f(x) = |x| в ряд Фурье в интервале (-1; 1).

f(x)

-2 -1 1 x

Функция четная, ряд Фурье содержит только косинусы, l = 1.

.

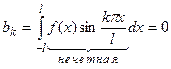Ряд (*) представляется в виде

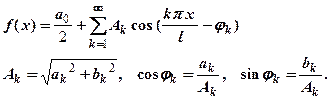
Комплексная форма ряда Фурье.

Рассмотрим ряд Фурье для функции, заданной в интервале (−π, π).

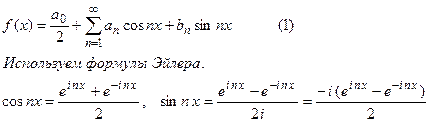
Если подставим эти формулы в ряд (1), то получим ряд по степеням e ^{i nx} и e ^{–i nx}

(n = 0; 1; 2; …). В общем случае этот ряд можно представить как ряд по степеням e ^{i nx}, где n = …-2; -1; 0; 1; 2; ….

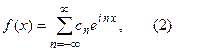
Для нахождения коэффициентов умножим ряд (2) на e ^{– i k x} и проинтегрируем от –π до π.

Если функция разлагается в ряд Фурье в интервале (-l, l), то комплексная форма ряда Фурье примет вид

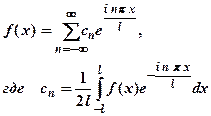
Известно, что если физический процесс описывается функциями

x(t) = A cos(ωt + φ) (3)

y(t) = A sin(φt + φ) (4)

то каждая из функций описывает гармоническое колебание с частотой ω, амплитудой А и фазой φ. В ряде случаев удобно вместо двух действительных функций (3) и (4) рассматривать одну комплексную функцию

z = x(t) + i y(t) = A (cos(ωt +φ) + i sin(ωt + φ)) = A e ^{i (ω t + φ)} = A e ^{i ω t} e ^{i φ} = Ce^{i ωt}.

С = А e ^{i φ} – комплексная амплитуда, |C| = A, arg C = φ.

По аналогии для ряда Фурье (2) называют комплексными гармониками. Числа
ω _n = ^{n π}/ _l называют волновыми числами (n = 0, ±1, ±2, ±3, ….)

Множество этих чисел называют спектром. Спектр дискретен.

Величину C _n называют комплексной амплитудой.

A_n = | C_n|, φ_n= arg C_n − амплитуда и фаза соответствующего гармонического колебания.

П р и м е р. Разложить в ряд Фурье в комплексной форме функцию f(x) = x в интервале (0, 2π)./ Построить график суммы ряда.

• • •

Дата добавления: 2015-07-02