Формальные логические модели

Фреймы

Термин фрейм (от английского frame, что означает «каркас» или «рамка») был предложен Маренном Минским [Минский, 1979], одним из пионеров ИИ, в 70-е годы для обозначения структуры знаний для восприятия пространственных сцен. Эта модель, как и семантическая сеть, имеет глубокое психологическое обо­снование.

Фрейм - это абстрактный образ для представления некоего стереотипа восприятия.

В психологии и философии известно понятие абстрактного образа. Например, произнесение вслух слова «комната» порождает у слушающих образ комнаты: «жилое помещение с четырьмя стенами, полом, потолком, окнами и дверью, пло­щадью 6-20 м²». Из этого описания ничего нельзя убрать (например, убрав окна, мы получим уже чулан, а не комнату), но в нем есть «дырки» или «слоты» - это незаполненные значения некоторых атрибутов - например, количество окон, цвет стен, высота потолка, покрытие пола и др.

В теории фреймов такой образ комнаты называется фреймом комнаты. Фреймом также называется и формализованная модель для отображения образа.

Различают фреймы-образцы, или прототипы, хранящиеся в базе знаний, и фрей­мы-экземпляры, которые создаются для отображения реальных фактических си­туаций на основе поступающих данных. Модель фрейма является достаточно универсальной, поскольку позволяет отобразить все многообразие знаний о мире через:

• фреймы-структуры, использующиеся для обозначения объектов и понятий (заем, залог, вексель);

• фреймы-роли (менеджер, кассир, клиент);

• фреймы-сценарии (банкротство, собрание акционеров, празднование име­нин);

• фреймы-ситуации (тревога, авария, рабочий режим устройства) и др.

Традиционно структура фрейма может быть представлена как список свойств:

(ИМЯ ФРЕЙМА:

(имя 1-го слота: значение 1-го слота), (имя 2-го слота: значение 2-го слота),

(имя N-гo слота: значение N-гo слота)).

Ту же запись можно представить в виде таблицы, дополнив ее двумя столбцами.

Таблица 1.1. Структура фрейма

Имя фрейма
Имя слота	Значение слота	Способ получения значения	Присоединенная процедура

В таблице дополнительные столбцы предназначены для описания способа полу­чения слотом его значения и возможного присоединения к тому или иному слоту специальных процедур, что допускается в теории фреймов. В качестве значения слота может выступать имя другого фрейма, так образуются сети фреймов. Существует несколько способов получения слотом значений во фрейме-экзем­пляре:

• по умолчанию от фрейма-образца (Default-значение);

• через наследование свойств от фрейма, указанного в слоте АКО;

• по формуле, указанной в слоте;

• через присоединенную процедуру;

• явно из диалога с пользователем;

• из базы данных.

Важнейшим свойством теории фреймов является заимствование из теории се­мантических сетей - так называемое наследование свойств. И во фреймах, и в се­мантических сетях наследование происходит по АКО-связям (A-Kind-Of = это). Слот АКО указывает на фрейм более высокого уровня иерархии, откуда неявно наследуются, то есть переносятся, значения аналогичных слотов.

Пример 1.4

Например, в сети фреймов на рис. 1.2 понятие «ученик» наследует свойства фреймов «ребенок» и «человек», которые находятся на более высоком уровне иерархии. Так, на вопрос «любят ли ученики сладкое» следует ответ «да», так как этим свойством облада­ют все дети, что указано во фрейме «ребенок». Наследование свойств может быть час­тичным, так как возраст для учеников не наследуется из фрейма «ребенок», поскольку указан явно в своем собственном фрейме.

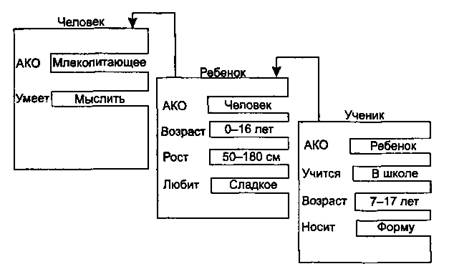
Рис. 1. 2. Сеть фреймов

Основным преимуществом фреймов как модели представления знаний является то,что она отражает концептуальную основу организации памяти человека [Шенк, Хантер, 1987], а также ее гибкость и наглядность.

Специальные языки представления знаний в сетях фреймов FRL (Frame Repre­sentation Language) [Байдун, Бунин, 1990], KRL (Knowledge Representation Lan­guage) [Уотермен, 1989], фреймовая «оболочка» Kappa [Стрельников, Бори­сов, 1997] и другие программные средства позволяют эффективно строить про­мышленные ЭС. Широко известны такие фрейм-ориентированные экспертные системы, как ANALYST, МОДИС, TRISTAN, ALTERID [Ковригин, Перфильев, 1988; Николов, 1988; Sisodia, Warkentin, 1992].

Традиционно в представлении знаний выделяют формальные логические модели, основанные на классическом исчислении предикатов 1-го порядка, когда предмет­ная область или задача описывается в виде набора аксиом. Мы же опустим описа­ние этих моделей по следующим причинам. Исчисление предикатов 1-го порядка в промышленных экспертных системах практически не используется. Эта логи­ческая модель применима в основном в исследовательских «игрушечных» систе­мах, так как предъявляет очень высокие требования и ограничения к предметной области.

В промышленных же экспертных системах используются различные ее модифи­кации и расширения, изложение которых выходит за рамки этого учебника.

Дата добавления: 2015-07-02