Структурний синтез автоматів з пам'яттю

Класмичним методом структурного синтезу цифрових автоматів зпамятью, заданих таблицями переходів і виходов, являється канонічний метод, який дозволяє звести задачу структурного синтезу довільних комбинаційнных схем. Канонічний метод структурного синтезу оперує з елементарними автоматами, які діляться на два великих класи.

Перший клас це елементарні комбінаційні автомати з памят`ю, які називаються елементами пам`яті.

Другий клас це елементарні комбінаційні автомати - логічні елементи.

Канонічний метод синтезу викорустовує структурно повний набір, який включає в себе елементарні автомати Мура, що володіють повною системою переходів і повною системою виходів, і будь-яку функціонально повну систему логічних елементів. Структурний синтез зводится до побудови такої схеми автомата, яка функціонує у відповідності іззаданними таблицями переходів и виходів автомата.

Алгоритм синтезу кінцевих автоматів з пам'яттю має наступний вигляд:

1. Складають початкове завдання функціонування, яке може мати різну форму, в тому числі і форму словесного опису.

2. Представляють автомат у вигляді графа або таблиці переходів і

виходів

3. Реалізують мінімізацію числа станів автомата.

4. Реалізують кодування станів автомата, вхідних і вихідних сигналів.

5. Реалізують вибір елементів пам'яті автомата (тип елементарних автоматів).

6. Вибирають структурно-повну систему елементів.

7. Реалізують побудову рівнянь булевих функцій збудження елементарних автоматів пам'ятфі і функцій виходів.

8. Будують структурну схему автомата.

Пункти 1,2,3 алгоритми синтезу кінцевих автоматів відносяться до абстрактного синтезу, а пункти 4,5,6,7,8 - до структурного синтезу автоматів.

Кодування вхідних, вихідних перемінних і станів автомата полягає в тім, що кожній букві X_і вхідного алфавіту {х₁, х₂,..., х_n} ставиться у відповідність сукупність значень фізичних сигналів Х^*₁, Х^*₂,..., X^*_r вхідного (двійкового) структурного алфавіту, а кожній букві у_і вихідного алфавіту Y = {у₁, у ₂,..., у_т} ставляться у відповідність сукупності значень фізичних виходів Y^*₁, Y^*₂,..., Y^*_r.

Кількість r входів і р виходів структурних автоматів при використанні двозначного структурного алфавіту визначається з умови

r ≥ log₂n, p ≥ log₂m,

де п і т - число букв у вхідному і вихідному алфавіті абстрактного автомата.

Кожному стану z, заданого автомата ставиться у відповідність сукупність станів Q₁, Q₂,..., Q_l елементарних автоматів. Кількість 1 елементарних автоматів при використанні двозначного структурного алфавіту визначається з умов

l ≥ log₂k,

де k - число станів автомата.

Роботу комбінаційних схем КС1 і КС2 (див. мал.4.2, 4.3) описують перемикаючі функції

q₁, q₂,…, q₂, y₁^*, y₂^*,…, y_p^*.

Кожна функція q_і визначає значення вхідного сигналу елементарного автомата в залежності від внутрішніх станів Q₁, Q₂,..., Q_l елементарних автоматів і від значень вхідних сигналів (фізичних) х^*₁, х^*₂,..., х^*_r і називається функцією збудження елементарного автомата Q_і

q _i = q _i (Q₁, Q₂, …, Q₁, x₁^*, x₂^*, …, x_r^*).

Значення аргументів і функції в цьому виразі визначені для того самого моменту дискретного часу, тому q є перемикаючою функцією. Для елементарного автомата, що має кілька входів, на етапі структурного синтезу варто одержати функцію збудження кожного його входу.

Кожна з функцій виходів y^*_jвизначає значення фізичного сигналу на j-му виході в залежності від внутрішніх станів елементарних автоматів і значень фізичних вхідних сигналів і називається функцією кодованих виходів автомата.

y _j ^*= y _j ^*(Q₁, Q₂, …, Q₁, x₁^*, x₂^*, …, x_r^*).

Функція кодованих виходів, так само, як і функція збудження, є перемикаючою функцією. Складність реалізації отриманих логічних функцій залежить від кодування станів абстрактного автомата. Розгляд питань раціонального кодування вхідних сигналів, станів і виходів автомата виходить за рамки дійсного навчального посібника. Тому варіанти кодування будуть вибиратися довільно. Для спрощення функцій збудження можна використовувати правило: чим більше переходів до стану z_i абстрактного автомата, тим менше одиниць повиннo бути в коді цього стану [3]. Подібне ж правило можна використовувати при кодуванні вихідних сигналів для мінімізації функцій виходів.

Кодування станів автомата необхідно виконувати так, щоб забезпечити відсутність небезпечних змагань (гонок).

Змаганнями називають явище неодночасної зміни сигналів на виходах логічних елементів унаслідок різної довжини логічних ланцюгів і різного часу затримки сигналів.

В асинхронних автоматах необхідно приймати спеціальні міри для усунення небезпечних змагань. Синхронні (тактуючі) автомати не піддані впливу критичних гонок унаслідок того, що зміна стану тактуючого автомата відбувається в момент надходження тактового імпульсу, причому перехід визначається значенням вхідних сигналів у попередній момент часу. Перехідні процеси звичайно закінчуються до моменту надходження наступного тактового імпульсу і не впливають на функцію переходів автомата.

Методику структурного синтезу автоматів розглянемо на прикладах.

ПРИКЛАД 1. Побудувати структурну схему автомата Мілі, заданого графом мал. 4.6.

1. Кодування станів автомата, вхідних і вихідних сигналів. Кількість елементарних автоматів /, необхідних для представлення трьох внутрішніх станів, визначається з умови

l ≥ log₂3, l = 2.

Вибираємо варіант кодування станів автомата відповідно до табл.4.19.

Таблиця 4.19

	Q1	Q2
Z1
Z2
Z3

Кількість фізичних входів r автомата, необхідних для представлення n вхідних букв, визначаємо з умови

r ≥ log₂2, z = 1.

Варіант кодування вхідних сигналів вибираємо відповідно до табл.4.20.

Таблиця 4.20

	X^*
X1
X2

Кількість фізичних виходів р автомата для представлення m вихідних букв визначаємо з умови

p ≥ log₂m, p = 2.

Варіант кодування виходів виберемо відповідно до табл.4.21.

Таблиця 4.21

	Y1^*	Y2^*
Y1
Y2
Y3

2. Типи елементарних автоматів, за якими будується схема, звичайно задаються. Припустимо, що елементарний автомат Q₁ є D-тригером, а автомат Q₂ є JK-тригером.

3. Як функціонально-повну систему елементів вибираємо елементи І, АБО, НІ

4. Для побудови рівнянь булевих функцій збудження елементарних автоматів пам'яті і функцій виходів складається кодована таблиця переходів і виходів автомата (табл. 4.22)

Таблиця 4.22

Номер рядка	t	t+1	t
X^*	Q1	Q2	Q1	Q2	D	J	K	Y1^*	Y2^*
								-
							-
								-
				-	-	-	-	-	-	-
								-
							-
								-
				-	-	-	-	-	-	-

Кодована таблиця переходів (табл. 4.22, стовпчика 2, 3, 4, 5, 6) визначає залежність станів елементарних автоматів Q₁^{t +1} іу момент часу t+1 від значень вхідних сигналів і внутрішніх станів елементарних автоматів у попередній момент часу.

Кодована таблиця виходів містить у собі стовпчики 2, 3, 4 табл. 4.22 і визначає значення вихідного сигналу в залежності від вхідних сигналів і станів елементарних станів.

У табл. 4.22 (стовпчики 2, 3, 4) приведені всілякі набори значень аргументів x*,Q₁, Q₂. Для заповнення стовпчиків 5 і 6 табл. 4.22 необхідно скористатися графом автомата і табл. 4.19. Розглянемо порядок заповнення табл. 4.22 на прикладі рядка 1. Значенню фізичного входу х* = 0 відповідає вхідний сигнал х₁ (див. табл. 4.20), а станам елементарних автоматів Q₁ =0,Q₂ =1 - стан Z₂ (див. табл. 4.19). За графом визначаємо, що сигнал х₁ переводить автомат зі стану Z₁, y стан Z₃. Звертаючсь знову до табл. 4.19, знаходимо стани елементарних автоматів, який закодований стан Z₃: Q₁= 1, Q₂=0 Ці значення записуємо в стовпчики 5 і 6 табл. 4.22.

За графом автомата визначаємо, що автомат, що знаходиться в стані Z₂, при надходженні сигналу Х₁ формує вихідний сигнал Y₃, Звертаючсь до таблиці кодування виходів (див. табл. 4.21), зауважуємо, що виходу Y₃ відповідають фізичні сигнали Y^*₁ =1 и Y^*₁ = 0 і заносимо ці значення в стовпчики 10 і 11 табл. 4.22 відповідно.

У рядках 3, 7.табл. 4.22 стан елементарних автоматів у момент часу t+1 і вихідний сигнал не визначені, оскільки стан, що має код Q₁ = 1, Q₂ = 1, відповідає. Ця комбінація при кодуванні станів не використовувалася.

Для складання функцій збудження елементарних автоматів використовуємо характеристичні таблиці (матриці переходів) D- і JK-тригерів, наприклад, відповідно до характеристичної таблиці D - тригера (див. табл. 4.7) у рядку 1, що містить перехід Q^t₁= 0 —> Q₁^t+1= 1 => D=1, в строке 2- Q^t₁=1 -> Q₁^t+1 =0=>D=0. Відповідно до характеристичної таблиці JK-тригера (табл. 4.14) у рядку 1(табл.4.22), що містить перехід Q^t₂ = 1 -> Q₂^t+1 = 0 => К = 1, J не визначено (значення J можна вибирати довільно). У рядку 2 табл. 4.22, що містить перехід Q^t₂ = 0 — >Q₂^{t+1 =} 1 => J=l, К не визначено. У такий же спосіб заповнюються інші рядки функцій збудження елементарних автоматів.

Вважаючи функції D,J,K, Y^*₁, Y^*₂ не цілком визначеними функціями аргументів ) Х^*,Q₁ и Q₂, визначаємо за допомогою карт Карно (мал. 4, 8, а, б, в, г, д) їхню мінімальну диз'юнктивну нормальну форму (МДНФ).

Рис. 4.8. Карти Карно функцій збеждення і виходів автомата: а - для D; б - для J; в - для К; г - для Y^*₁; д - для Y^*₂

5. Структурну схему автомата (мал. 4.9) будуємо по системі функцій, отриманих за допомогою карт Kapно:

Рис. 4.9. Логічна схема автомата

ПРИКЛАД 2. Побудувати структурну схему автомата Мура на логічних елементах, АБО-НІ заданого відзначеною таблицею переходів (табл. 4.23).

1. Кодуємо стани автомата, вхідних і вихідних сигналів.

Варіант кодування станів автомата представлений табл. 4.24, вхідних - табл. 4.25, вихідних - табл. 4.26. Для цього автомата можна прийняти: 1 = 2, r=l, p = 2.

Таблиця 4.23

Вихдний сигнал	y1	y2	Y3	Y2
Стан	z1	z2	z3	z4
Вхідний сигнал	x1	z1	z4	z1	z4
x2	z2	z2	z3	z3

Таблиця 4.24

	Q1	Q2
Z1
Z2
Z3
Z4

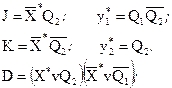
2. Як елементарний автомат Q₁ вибираємо JK-тригер, а як елементарний автомат Q₂ вибираємо D-тригер.

3. Як функціонально-повну систему елементів вибираємо АБО-НІ.

4. Складаємо кодовану таблицю переходів і виходів автомата (табл. 4.27).

Таблиця 4.27

Номер рядка	t	t+1	t
X^*	Q1	Q2	Q1	Q2	J	K	D	Y1^*	Y2^*
							-
							-
						-
						-
							-
							-
						-
						-

5. Визначаємо за допомогою карт Карно (мал. 4.10) мінімальну кон'юнктивну нормальну форму функцій J, К, D аргументів x*,Q₁, Q₂ і функції у^*₁, у^*₂ аргументів Q₁, Q₂.

Рис. 4.10. Карти Карно функцій порушення і виходів автомата: а - для J; б - для К; в - для D; г -для Y^*₁;д -для Y^*₂

6. Оскільки як функціональну систему елементів обрані елементи АБО-НІ то функції J, К, D, у^*₁, у^*₂ варто перетворити до виду:

Перетворення функцій J, К, D, у^*₁, у^*₂ виробляється по теоремі ДЕ Моргана.

7. Структурну схему автомата (мал. 4.11) будуємо по системі функцій, отриманих у п.6.

Рис. 4.11. Структурна схема автомата

Таблиця 4.25

	Y1^*	Y2^*
Y1
Y2
Y3

Таблиця 4.26

	X^*
X1
X2

Дата добавления: 2015-06-27