Кладбище Серпинского

Задача 2.

Задача 1.

Исследовать на непрерывность функцию, заданную на отрезке [0,1] следующими равенствами:

1. 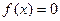при ;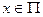

2. 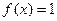в середине смежного интервала;

3. Для точек смежного интервала 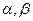( 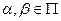поэтому, 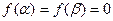, 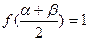) функция 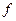определяется как линейная 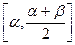на и на .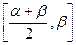

Решение. На первый взгляд рассматриваемая функция является непрерывной, кажется, что мы просто “строим линейные крышки”, “затыкая” промежутки в множестве Кантора. Левая картинка только усиливает эту мысль, но правая дает понять, что это не так.

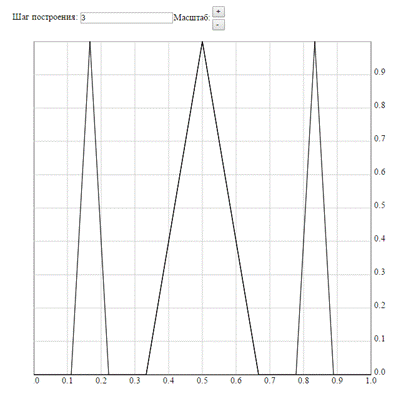
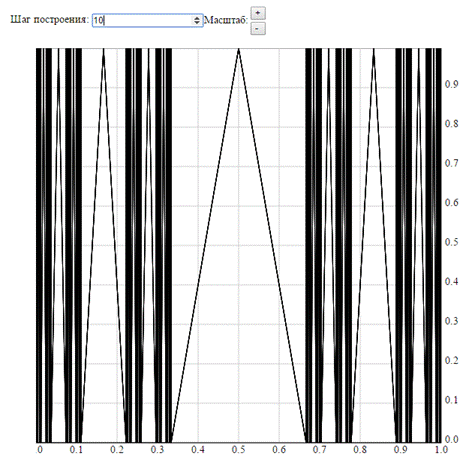
Действительно, на смежных интервалах функция непрерывна. Поэтому остается исследовать ее на пределы в точках множества Кантора. Любу. Точку множества Кантора можно получить как предел точек множества Кантора (т.к. в любой окрестности их нечетное число), так и как предел середин смежных интервалов (т.к. в любой окрестности найдется смежный интервал). Далее, так как предел по точкам из множества Кантора равен нулю, а по серединам смежных интервалов – единице, то получаем, что в точках множества кантора функция 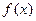терпит разрыв.

Отметим однако, что в точках множества кантора первого рода (за исключением точек 1 и 0) со стороны смежного интервала предел функции существует и равен 0. Поэтому мы можем только говорить об односторонней непрерывности в данных точках.

Существует ли непрерывная функция, которая “пересекает ось абсцисс” несчетное число раз?

Функция 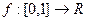непрерывна. Будем говорить, что функция “пересекает ось абсцисс” в точке x, если выполнено:

1. f(x)=0;

2. в любой окрестности точки x найдутся точки y и z такие, что f(y)<0, f(z)>0

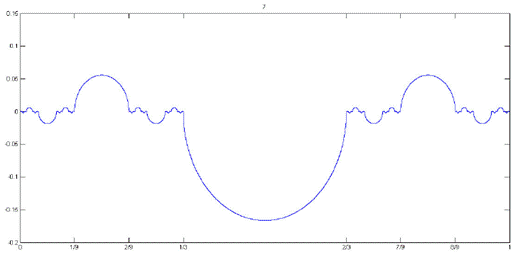
Решение. Да, существует. Проведем построение графика искомой функции f(x) на счетное число шагов. На нулевом шаге кладем f(x) = 0 при всех 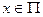. На первом шаге построим нижнюю полуокружность на смежном интервале первого ранга, как на диаметре. На втором шаге построим верхние полуокружности на двух смежных интервалах второго ранга, как на диаметрах. На третьем шаге построим нижние полуокружности на четырёх смежных интервалах третьего ранга, и т.д., на (2n-1)- ом шаге строим нижние, а на 2n -ом шаге верхние полуокружности на смежных интервалах (2n-1)- го и 2n -го рангов, соответственно, и т.д. счётное число раз.

Построенная функция f(x) обращается в нуль в континууме точек множества 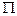. И, сколь угодно близко от точки из 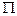найдутся смежные интервалы (2n-1)- го и 2n -го рангов, на которых 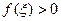и 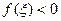соответственно.

2 Совершенные нигде не плотные множества на плоскости [7]

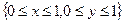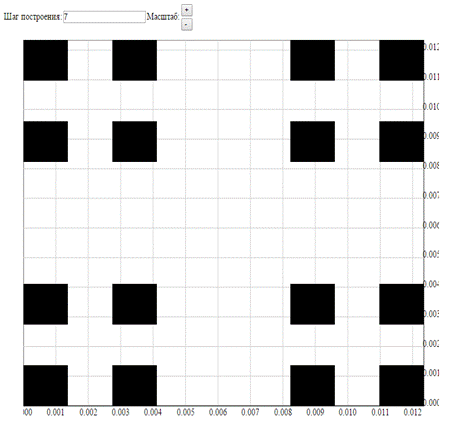
Построим на плоскости интересное множество В следующим образом: разделим, квадрат прямыми 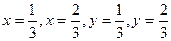на 9 равных квадратов и выбросим их них пять открытых, не примыкающих к вершинам исходного квадрата. Затем, каждый из оставшихся квадратов также разделим на 9 частей, и выбросим пять из них, и т.д. Множество, оставшееся после счётного числа шагов, обозначим B и назовём кладбище Серпинского. Вычислим площадь выброшенных квадратов:

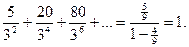
Кладбище Серпинского является совершенным и нигде не плотным множеством.

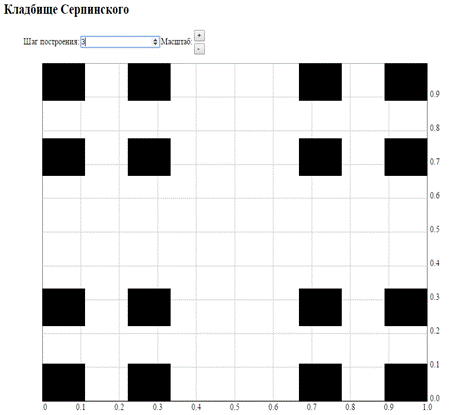
Заметим фрактальную структуру множества.

Дата добавления: 2015-06-27